中文标题:AlphaGo Zero:无师自通的围棋大师
英文标题:Mastering the game of Go without human knowledge
发布平台:Nature
发布日期:2017-10-01
引用量(非实时):8443
DOI:10.1038/nature24270
作者:David Silver, Julian Schrittwieser, Karen Simonyan, Ioannis Antonoglou, Aja Huang, Arthur Guez, Thomas Hubert, Lucas Baker, Matthew Lai, Adrian Bolton, Yutian Chen, Timothy Lillicrap, Fan Hui, Laurent Sifre, George van den Driessche, Thore Graepel, Demis Hassabis
文章类型:journalArticle
品读时间:2023-02-16 14:07
1 文章萃取
1.1 核心观点
- AlphaGo Zero 通过融合蒙特卡洛树搜索与深度神经网络,用神经网络指导搜索算法的策略生成,通过又借助对弈结果反过来改进神经网络。此外AlphaGo Zero 还使用一个神经网络同时给出状态的价值评估和策略的概率分布预测,兼具了准确性和训练效率。最终 AlphaGo Zero 在没有人类知识注入的情况下,依靠自我对弈的强化学习,在围棋方面以100-0的战绩打败了之前发布AlphaGo(而当时的AlphaGo已经打败了人类的顶尖围棋选手)
1.2 综合评价
- 论文内容明确分割为两部分,第一部分重视阐述模型的改进思路,突破性与评价;第二部分则将很多算法细节和其他补充内容进行了陈列。整体内容详略得当,表达清晰
- 将传统搜索算法和深度神经网络进行融合,互相补充与促进,思路十分地优雅
- 验证全面,分析深刻,尤其是在挖掘AlphaGo Zero 在无师自通的情况下的棋风与人类行为的相似性和差异性(这方面的工作感觉也是非常繁复的)
1.3 主观评分:⭐⭐⭐⭐⭐
2 精读笔记
2.1 背景介绍
tabula rasa是拉丁文中”白板”的意思,原指一种洁白无瑕的状态。本文提出的AlphaGo Zero的最大特点,便是在没有前提知识注入的情况下,仅通过神经网络和强化学习,实现了机器学习并超越人类顶尖水平的围棋能力
围棋的基本规则补充(大陆版):
- 围棋盘面纵横各有19条等距平行线,构成了361个交叉点
- 棋子分黑白两色,现代为黑先,古代为白先,一般黑白子各180颗
- 先后手可以由抽签、猜先或棋赛规则确认
- 轮流下子是双方的权力,但允许任何一方放弃下子权
- 棋子紧邻的空点是这个棋子的气;紧邻的同色棋子之间气是共享的;失去所有气的棋子成为“无气”或“死子”,反之为“有气”或“活子”
- 把无气之子提出盘外的手段叫做“提子”;下子后,应立即提取对方无气之子
- 一场棋局的结束一般包括三种情况:1.对局中的一方中途认输 2.双方连续使用虚着(放弃下子权) 3.双方一致确认着子完毕
- 中国大陆的围棋采用数子法的方式来决定胜负,棋局结束之后,先将双方在棋盘中的死子全部清除,之后计算双方的活棋及活棋围住的点;双方活棋之间的空点各得一半;点数大于180.5的一方获胜,等于180.5时为和棋
围棋的相关小知识:
- 拿⼦⽅法:以⾷指和中指的指尖夹住棋⼦(中指在上、⾷指在下)
- 猜先:高段者先手握若干白子暂不示人,之后低段者出示1颗或2颗黑子(以表示猜奇偶),猜对则低段者先手;同段者由年长者握子
其他算法方向的已有探索
- NeuroGo 使用神经网络来表示价值函数,并构造了很复杂的架构来注入有关连接性,疆域和眼的围棋知识,该神经网络通过时间差分学习进行训练,最终达到了业余段位水平
- RLGO44 详尽列举所有棋子的3×3特征,并使用了特征的线性组合来表示价值函数,也通过时间差分学习进行训练,最终达到了业余段位水平
- 蒙特卡洛树搜索 MCTS 也可以看作一种自我博弈强化学习,曾在围棋领域达到了较强的专业段位水平,但使用了大量领域专业知识
- 其他领域(棋牌类、电子游戏类)一般的训练方式也都是时间差分学习、回归、或利用自我博弈的数据进行训练,也有的使用已有的计算机程序来进行训练或生成游戏记录;策略评价一般使用Alpha-beta剪枝、蒙特卡洛搜索、反事实的遗憾最小化(CFR)算法
时序差分算法 TD:用基于当前奖励和下一状态的预估价值来替代当前状态在完整序列中的预估收益,最终得到的是当前状态价值的有偏估计;但因为不需要等待结果就能更新,所以更快速、灵活,最终效果也一般更好
Alpha-beta剪枝:一种对抗性搜索算法,是对极小化极大算法(以递归形式,找出失败的最大可能性中的最小值)的改进,主要通过树结构及剪枝策略避免不合理方向的递归
反事实的遗憾最小化(CFR):使用反事实值(正比于遵循特定策略后,达不到预期状态的概率)作为遗憾值的收益,以遗憾值最小为原则更新动作空间的概率分布
第一版AlphaGo在2015年10月击败了欧洲冠军樊麾(蝉联2013年至2015年的三届欧洲围棋冠军),因此在本文中可称其为AlphaGo Fan;第二版AlphaGo在2016年3月击败了曾获得18次国际围棋冠军的李世石,因此在本文中可称其为AlphaGo Lee;第三版AlphaGo未曾公开,但和AlphaGo Zero使用了相关的算法和架构,只不过接受了人类知识的注入,最新性能远超于前两者,2017年1月在网络对弈中以60-0的成绩击败其中最强者,在本文中可称其为AlphaGo Master
已有模型的缺点:依赖于专家数据(获取成本高,数据不可靠)
2.2 前置知识
AlphaGo Fan 的模型细节:
- 包含两个结构相同的深度神经网络,一个策略网络用于输出移动概率,一个价值网络用于输出棋盘状态的价值评估。
- 在AlphaGo Fan 的训练过程中,算法首先会结合蒙特卡洛树搜索 MCTS 提供前瞻搜索,之后策略网络将搜索范围收拢个几个高概率的落子位置,最后价值网络会结合基于蒙特卡洛模拟的推演结果对这些落子策略进行价值评估
- 策略网络训练的第一阶段是针对人类专家的动作预测的有监督学习,对应的目标函数是最大化在状态$s$下选择动作$a$的可能性。最后模型的训练参数会用于第二阶段训练前参数初始化
- 策略网络训练的第二阶段是通过策略梯度强化学习(policy-gradient reinforcement learning)进行增强,即随机选取一个之前迭代的旧版策略网络与当前的策略网络进行对弈(防止过拟合)。之后将胜利者对应的历史动作序列赋予奖励+1,失败者对应的历史动作序列赋予奖励-1,而此阶段的训练目标是追求最大化预期奖励
- 价值网络的强化学习:在通过策略网络进行自我对弈的过程中,价值网络会通过预测游戏的输赢实现训练,目标函数是预测结果与真实胜负之间的均方误差最小;需要注意的是使用完整的对弈数据会导致过拟合(一个动作前后的棋盘状态是紧密相关的),因此需要额外采样生成一个稀疏的自我对弈数据集,此方法最终预测效果更准确,同时计算量只有原来的1/15000(避免了前瞻搜索中蒙特卡洛的模拟推演过程)
AlphaGo Lee 的程序之前未公布,但大部分都与AlphaGo Fan 是一致的。只不过AlphaGo Lee 使用了更大的策略网络和价值网络(12个卷积层,每层有256个特征平面 planes),除此之外AlphaGo Lee 还将原本AlphaGo Fan 中价值网络的训练数据由策略网络的自我对弈改为AlphaGo 的自我对弈(个人推测是在执行动作前增加了蒙特卡洛的模拟推演过程)
AlphaGo Fan 训练使用了176个GPU,而AlphaGo Lee 训练使用了48个TPU(所以能实现更快的搜索速度,也进行了更多的迭代次数);二者都进行了分布式训练
AlphaGo Master使用了和AlphaGo Zero使用了相关的算法和架构,同时融合了AlphaGo Lee 所使用的手工特征和蒙特卡洛模拟过程,并使用人类专家数据进行初始化训练
AlphaGo Zero的特性:
- 不需要人类数据和监督数据,仅需要自我对弈
- 输入特征只使用棋盘及其黑白落子分布
- 只使用单一神经网络,而不是单独的策略/价值网络
- 提出了更简单的树搜索方法,并不再需要蒙特卡洛模拟
- 引入了新的强化学习算法,将前瞻搜索纳入训练循环
2.3 算法细节
深度神经网络定义:$(p,v)=f_{\theta}(s)$
- $f_{\theta}$表示深度神经网络,网络参数为$\theta$;
- 输入为$s$(当前棋盘的状态表示,也包括一系列历史状态的表示);
- 输出包含两部分:概率分布$p$(描述下一步落子位置的概率分布)和价值$v$(评估玩家在状态$s$时的获胜概率)
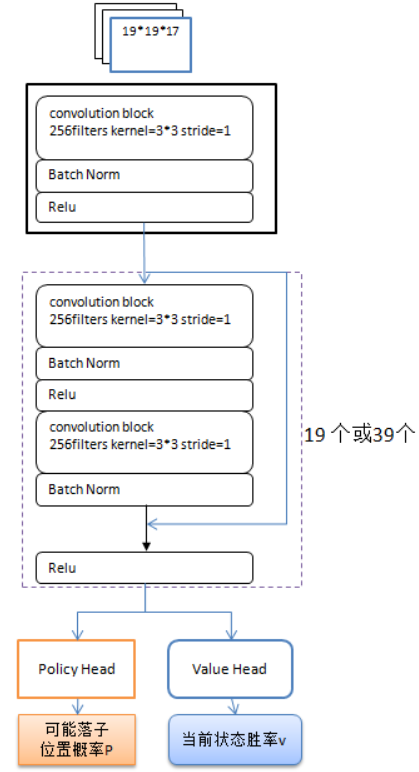
深度神经网络构成:
- 输入维度为$19\times 19\times 17$,其中$19\times 19$为棋面的维度,17层特征则包括执黑行棋的8个历史状态(仅标识黑子)、执白行棋的8个历史状态(仅标识白子),以及单独一个特征用于标识当前的行棋方(黑色执棋则全为1,黑色执棋则全为0)
- 网络结构主要包含20个残差块组成的卷积层
- 每个残差块都包含具有256个滤波器,核大小为3×3,步长为1的卷积层
- 每个残差块使用批次归一化和非线性映射(Relu)技巧
- 针对概率预测和胜率预测,分别额外添加两层和三层(全连接层?)
蒙特卡洛树结构:
- 搜索树的每条边记为$(s,a)$,表示在状态$s$下选择动作$a$
- 每条边存储三个值:先验概率$P(s,a)$,访问次数$N(s,a)$,动作平均价值$Q(s,a)$,动作累积价值$W(s,a)$(这个累积价值不是很重要,只是为了动态计算$Q$更方便)
蒙特卡洛树搜索(MCTS):
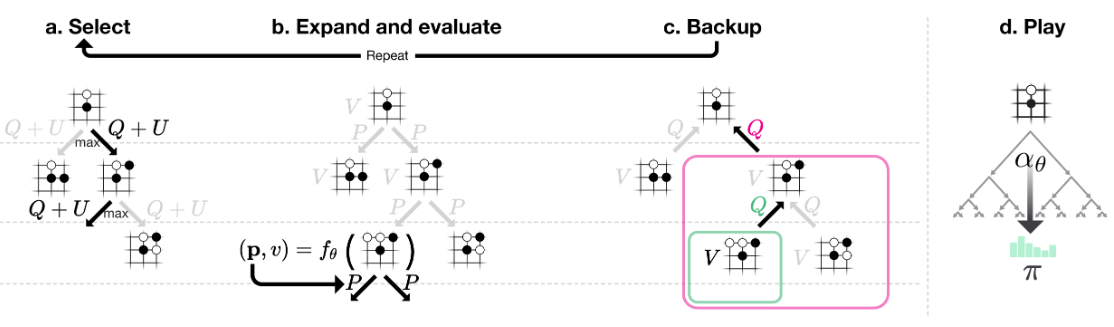
- 每次模拟从根节点开始,以最大化置信上限$Q+U$为原则选择子节点
- 其中$U(s,a)=c_{puct} P(s,a) \frac{\sqrt{\Sigma_b N(s,b)}}{1+N(s,a)}$,随访问次数增加而逐步衰减,使得模型在早期倾向于探索,而在后期更偏向于价值高的动作;其中$c_{puct}$是用于设定探索水平的常数
- 对于每个新拓展的子节点$s'$,可以先直接计算得到深度神经网络的输出:
$$(P(s',.),V(s'))=f_{\theta}(s')$$
- 其中$P(s',.)$作为输出的概率分布,将存储在从$s'$节点出发的每一条边中
- 伴随着模拟次数$N(s,a)$的增加,动作价值$Q(s,a)$将更新为这些子节点的平均价值:
$$Q(s,a)=1/N(s,a)\Sigma_{s'|s,a\to s'}V(s')$$
- 上式中,$s,a \to s'$表示从状态$s$经过动作$a$后到达状态$s'$(节点$s$的任意子节点)
- 给定神经网络参数$\theta$和根节点状态$a$后,MCTS能给出一个最优的搜索策略$\pi$,为方便带入参数,在本文中也会用函数$\alpha$来表示:$\pi= \alpha_{\theta}(s)$
- 策略$\pi$中的落子动作$a$对应的搜索概率为$\pi_a$,其正比于每个落子动作的访问次数的指数:
$$\pi_a\propto N(s,a)^{1/\tau}$$
- 其中$\tau$为用于控制探索水平的温度参数,在AlphaGo Zero的设计中,会在每局游戏/对弈的前30个动作时设为$\tau=1$,而在其他时候$\tau\to 0$(确保选择具有最大访问数的落子)
神经网络的自我强化学习:
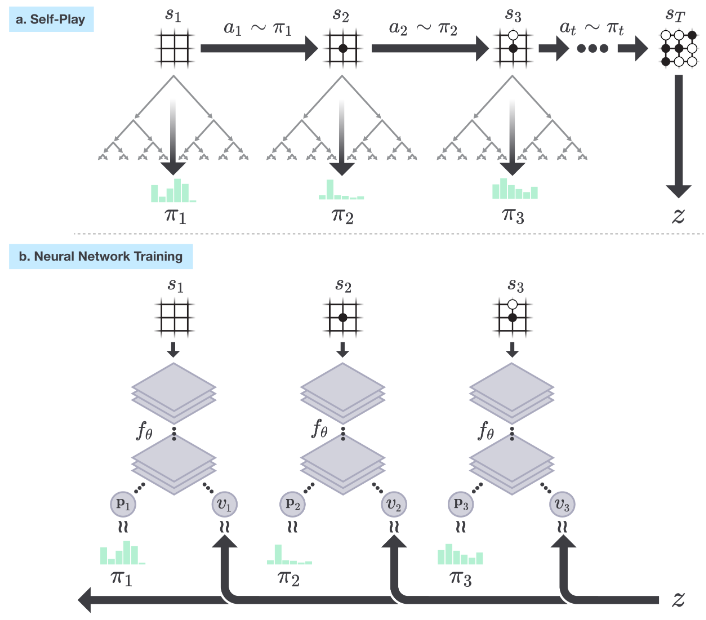
- 训练需要借助 MCTS 的输出结果,即每个落子动作的搜索概率(MCTS作为一种策略改进算子(policy improvement operator),输出的概率比初期的神经网络可靠很多)
- 假设模拟的自我对弈过程为${s_1,s_2,s_3,...,s_T}$,其中第$t$步的状态为$s_t$,最后一步的状态为$s_T$,此时对应的游戏胜利者设为$z$
- 神经网络的初始权重为$\theta_0$,经过$i-1$次自我对弈(迭代)后,网络参数更新为$\theta_{i-1}$,之后在第$i$次迭代的第$t$步时,MCTS会根据神经网络$f_{\theta_{i-1}}$和状态$s_t$给出搜索策略$\pi_t$:
$$\pi_t=\alpha_{\theta_{-1}(s_t)}$$
- 根据策略$\pi_t$给出的概率进行随机落子,自我对弈的结束条件有三种:1.双方都选择不落子(pass) 2.搜索的价值低于预设的阈值 3.对弈次数达到预设的最大值
- 对弈结束时,需要根据比赛计分给出最终奖励$r_{T}\in {-1,+1}$;而在每一个时间步$t$都有数据存储:$(s_t,\pi_t,z_t)$,其中$z_t=\pm r_T$(正负号取决于对弈的玩家视角)
- 神经网络参数会根据数据$(s,\pi,z)$更新为$\theta_i$,更新原则包含两部分:1.使预测值$v$与实际比赛赢家$z$之间的尽可能一致(均方误差最小) 2.使预测概率$p$与实际搜索概率$\pi$尽可能相似(交叉熵最小):
$$(p,v)=f_{\theta}(s)\ \ and \ \ l=(z-v)^2-\pi^Tlogp+c||\theta||^2$$
- 其中$c$是一个控制$L2$正则化水平的超参数(本文中设定为$10^{-4}$),用于防止模型的过拟合
自我强化学习算法解析:
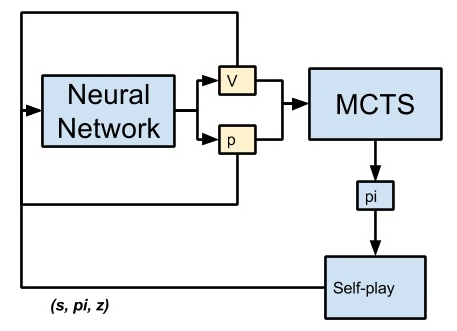
- AlphaGo Zero 的策略改善从一个神经网络策略开始
- 基于该神经网络策略的 MCTS 反复进行落子动作的推演模拟,提供了丰富的自我对弈数据(具有最大平均价值的动作提供了一个训练的正例样本,而其他的动作提供了训练的负例样本)
- 自我对弈的结果也由此投射回神经网络的函数空间,即调整网络参数来更好地匹配博弈结果,包括搜索概率(交叉熵)和预测胜负(均方误差)
2.4 模型训练
AlphaGo Zero训练相关细节:
- 使用具有4个TPU的单机,整体训练时长大约是3天
- 训练过程中,每次MCTS模拟1600次,生成了490万场自我博弈
- 每次落子使用约0.4s的思考时间(主要用于MCTS的1600次模拟)
- 神经网络包含20个残差块,并行迭代了$2048\times 70$万次
用于对比的有监督模型:
- 为方便对比,采用了和AlphaGo Zero使用相同的神经网络架构
- 基于KGS数据集预测专业选手的动作,效果比以往的有监督建模都要好
- 但与AlphaGo Zero仍存在差距,在训练24小时后被反超
用于验证极限表现的AlphaGo Zero 40 blocks:
- 神经网络参数翻倍,使用40个残差块
- 耗时超过40天,并行迭代了$2048\times 410$万次
其他训练过程中的细节:
- 围棋规则在旋转和对称下是不变的,借此可以做数据增强
- 围棋规则在棋子颜色调换后也是不变的,借此可以做数据增强
- 使用高斯过程优化选择MCTS搜索的超参数,提高自我对弈性能
- 自我博弈训练流程的三个主要组成部分(基于自我对弈数据进行神经网络参数的优化、对模型进行棋手水平的评估、生成最新的自我对弈数据)都可以并行地异步执行
- 学习率策略:动量法+退火(随着训练的进行,学习速率从$10^{-2}$逐渐减小为$10^{-4}$)
- 每进行1000次训练,就会产生一个检查点,用于评价与自我对弈数据的生成
- 为了保证前期模型能进行充分的探索,在根节点的先验概率中加入狄利克雷(Dirichlet)噪声,确保初期的所有落子可能都会被尝试一遍:$p=p(1-\epsilon)+\epsilon \eta$ 其中$\eta \sim Dir(0.03), \epsilon=0.25$
- 为了节省运算量并更贴近实际情况, 模型会在显然会输的局面下选择弃权;弃权对应的阈值需要额外测定,原则是保持误报率(放弃本来能赢的局面)低于5%
2.5 结果分析
最终效果评价:
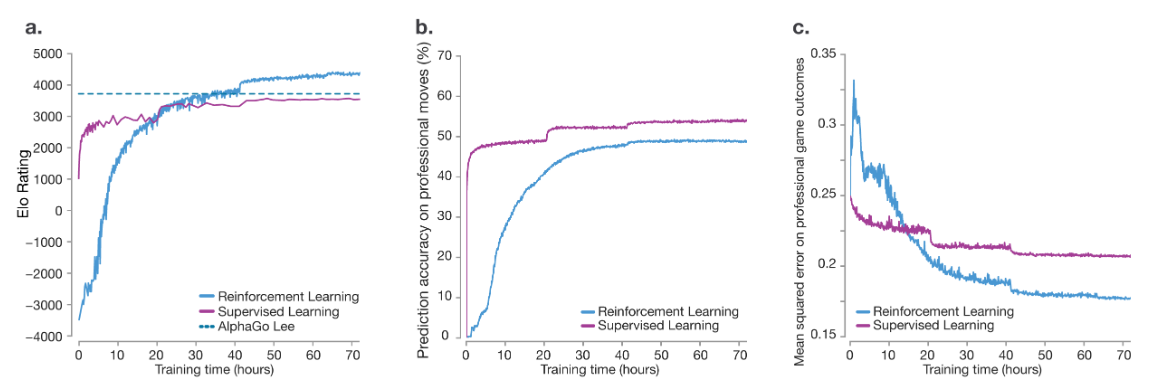
- 上图中,横坐标均表示训练时长;蓝色实线表示AlphaGo Zero;紫色实线为基于人类知识(KCG数据集)进行有监督训练得到的对比模型;蓝色虚线为AlphaGo Lee的积分水平
- 图a中纵坐标表示ELO评分(用于评价对弈者的水平),其中可以发现虽然有监督学习初期进步更快,但很快就被AlphaGo Zero超越;在训练36小时后,AlphaGo Zero的性能超过了AlphaGo Lee;在训练72小时后,AlphaGo Zero能够以100比0击败AlphaGo Lee
- 图b中纵坐标表示模型预测人类棋手落子的准确率,AlphaGo Zero的预测能力在逐渐逼近基于人类知识进行有监督训练得到的对比模型(最后仍存在差距,可能是思路已经超越人类了?)
- 图c中纵坐标表示模型在人类职业比赛结果上的均方误差(MSE),在训练约16小时后AlphaGo Zero的实战表现就已经开始超越有监督的对比模型,最终表现也遥遥领先
- 落子的准确率和比赛实战均方误差的统计,都是基于gokifu数据集(开源的棋谱数据)
ELO等级分制度:是美国物理学家 Arpad Elo 创建的一个衡量各类对弈活动选手水平的评分方法,是当今对弈水平评估的公认的权威方法。被广泛应用于国际象棋、围棋、足球等运动,以及很多网游与电子竞技产业。
ELO评分计算方法:假如玩家A的积分为$R_A$,玩家B的积分为$R_B$;则玩家A对决玩家B的预期胜率为$1/(1+10^{(R_b-R_a)/400})$,如果实际胜率为$S_a$(胜1负0平0.5),则玩家A进行积分的更新: $$R'_a=R_a+K(S_a-E_a)$$ 其中$K$为常数项,数值越大则积分的波动越大(大师级象棋赛通常取16)
模型贡献度分析:

- 为了更好地区分算法策略与网络结构对最终效果的贡献,本文按照算法策略的不同(策略网络和价值网络共享 dual VS 策略网络和价值网络独立 sep)和网络结构的不同(残差网络 res VS 卷积网络 conv)分别训练了四个神经网络,并进行对比分析
- 四个神经网络使用相关的损失函数与训练集数据(均来自AlphaGo Zero的72小时自我博弈)
- 用残差网络替换卷积网络,以及策略网络和价值网络共享,这两处改善均对ELO评分有显著提高作用(图a),也会显著降低模型在人类职业比赛结果上的均方误差(图c)
- 策略网络和价值网络的合并会略微降低模型针对棋手落子的预测准确率,而残差网络会显著提高落子预测准确率;不过这两个网络的合并会大幅提高计算和训练效率
AlphaGo Zero的潜力挖掘——AlphaGo Zero 40 blocks:

- 使用40个残差块的AlphaGo Zero模型效果打败了之前最出色AlphaGo Master
- 上图中,Raw Network表示仅使用神经网络(不使用MCTS模拟)的AlphaGo;ZeroCrazy Stone,Pachi和gnugo都是以前的围棋程序
- 需要注意的是,ELO评分高于200点就意味着预期胜率达到了75%;而最终AlphaGo Zero与AlphaGo Master的对弈成绩为89:11,胜率为89%
AlphaGo Zero在自我博弈训练过程中的成长:
- 对围棋概念有了深奥理解,包括但不限于布局、妙手、活与死、劫(重复的棋面,类似于无穷循环)、收官(围棋的最后一个阶段,双方竞逐边界的小地方)、提子、对杀(双方棋子互相包围,并且都没有做成活棋。只有去杀对方,才能做活)、先手、棋形、棋势、实地(黑棋围住而无法被侵略的区域)/厚势(白棋围住而无法被侵略的区域)
- 值得一提的是,征子(又称扭羊头,利用对方棋子只有一口气,通过不断扭拐叫吃的吃子方法)作为一种比较基本的围棋走法,AlphaGo Zero是在训练很久后才掌握
- 在训练3小时后,模型像人类初级棋手一样专注于吃子;在训练19小时后,模型初步掌握了活与死、棋势、实地/厚势等概念;在训练46小时后,模型频繁使用在人类职业赛事中很常见的3-3定式(落子占据并确保角落的安全);在训练70小时后,模型的自我对弈变得平衡而精彩(包括多场战斗和复杂的劫争)
- 通过自我对弈,AlphaGo Zero不仅掌握了围棋知识的基本要素,还发现了围棋的新境界,开拓了传统围棋知识的范围(这一点在事实上也得到了很多世界顶尖棋手的认可)
围棋的知识经过千年的积累与沉淀,几代人的传承才有了今日的底蕴
而AlphaGo Zero从零开始,在短短的几天内便能够走完这段旅程,并实现突破~
不过AlphaGo Zero依然需要手动设定一些基本规则,比如围棋的禁手、可行的动作候选序列、胜利规则等
 图源:
图源: