1 小批量梯度下降回顾
Overview of mini‐batch gradient descent
复习:误差曲面
1.1 全批量学习 full batch learning
对满足碗状的目标函数来讲,梯度的方向大致指向最优解的方向,但椭圆越扁,偏离越多。只有在圆形时,梯度才精确地指向圆心。
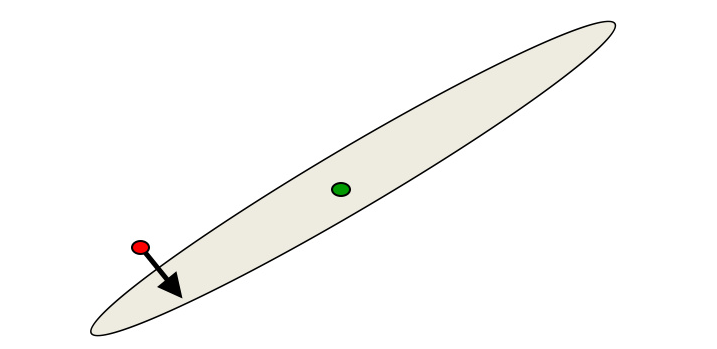
- 上图中梯度在正确方向的分量非常小,而在错误方向上的分量非常大
- 对线性系统来讲,这种梯度下降不是个好主意。即便对非线性的多层神经网络来讲(哪怕其error surface整体上不是碗状),也存在这个问题。
- 多层神经网络的error surface在一些方向上类似二次曲线,另一些方向上则不是。
可能存在的问题:模型的不收敛
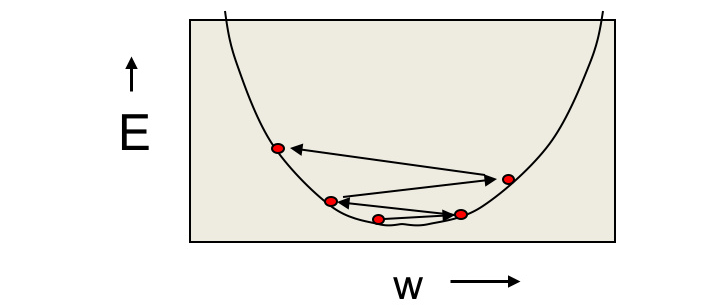
- 如果学习速率太高,权值将会在二次曲线中来回震荡
- 从立体的角度来讲,就是在峡谷里来回震荡而不收敛
- 理想的训练过程是沿着峡谷下降的方向快速穿越峡谷
- 在梯度稳定的方向快速前进,而在梯度不稳定的方向缓慢移动
1.2 随机梯度下降
如果一个数据集所包含的信息是高度冗余的,那么数据集前半部分计算所得的梯度应该非常接近数据集后半部分计算所得的梯度。而极端的来想,每次梯度计算只考虑一个样本,也是可以的。这也被称为”online learning“
不过一般来说小批量梯度下降要优于单样本梯度下降
- 更新权重所需要的计算量更好
- GPU很适合处理矩阵的并行计算
- 使用mini-batch需要注意样本的类别平衡(顺序不敏感的数据可以考虑直接随机打乱数据集),不然有可能导致模型陷入某种偏见
1.3 两种学习算法分析
全量梯度下降
- 存在很多经典的加速技巧,例如非线性共轭梯度法(non-linear conjugate gradient,NCG) https://keson96.github.io/2016/11/27/2016-11-27-Conjugate-Gradient-Method/ #待补充 )
- 但多层神经网络并不是现有算法的典型适用对象,所以还需要很多修改
小批量梯度下降法
- 在面对样本较多或信息存在冗余的数据集时更合适
- 也可以进行加速,但需要每次的min-batch更大一些
- 相比于全局梯度下降,计算效率更好
1.4 如何设定学习速率
- 随机设定学习速率:当模型误差一直变差或反复震荡时候需要缩小学习速率,当模型误差稳定下降但过于缓慢时增大学习速率
- 可以通过程序自动实现第一步提及的学习速率自适应
- 在模型训练快结束的时候,应该适当缩小学习速率:减少多个mini-batch切换引起的震荡
- 当模型误差停止减少时候,应该适当缩小学习速率:注意误差应该是验证集误差而不是训练集误差
2 小批量梯度下降的相关技巧
A bag of trickss for mini-batch gradient descent
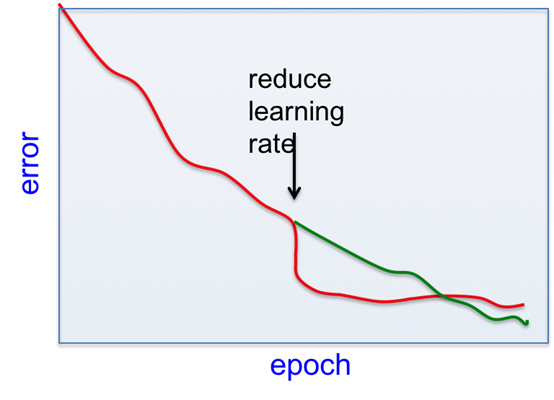
2.1 不要过早减小学习速率
较小的学习速率可以减少不同mini-batch之间随机的error波动,所以有立竿见影的效果。但之后的学习会变慢,反而导致最终得不偿失。
2.2 权重初始化
- 如果两个隐藏层神经元的进出权值和bias都是相同的,则两者的权重更新都会受到相同的梯度影响,即训练过程中的更新也是一致的
- 最终它们其实还是同一个feature detector,无法学习到不同的feature
- 随机初始化的目的是使对称失效(symmetry breaking)
- 如果神经元的输入值量级很大,那权重的很小变动就可以引起结果的巨大变化;所以这种情况下权重初始化应该尽可能小一点
- 学习速率也可以参考类似的思路进行量级的调整
2.3 输入的平移

- 通过平移保证输入值的均值为0,往往会有益于模型
- 如上图所示,平移使得误差曲线更接近正圆,模型也更容易收敛
- 类似的思路也可以用在激活函数上,双曲线切线$y=tanh(x)$的激活值就符合均值为0的情况,这是它优于
logitic函数的一点
2.4 输入的缩放

- 调整输入的方差为1(或者约束数据的范围)
- 从误差曲线上看,能起到类似于输入平移的作用
2.5 更周密的方法
对于线性神经元来说,去掉输入维度之间的相关性是非常重要的
比如主成分分析(Principal Components Analysis,PCA)
- 弃置特征值过低的维度(实现降维)
- 把剩下的维度除以特征向量的平方根(类似缩放/标准化)
- 最终的误差曲线将会是一个优秀的圆形
- 梯度也将直接指向圆心
2.6 多层神经网络的常见问题
初始学习率特别大
- 将导致每个隐藏层神经元权值的绝对值变大
- 此时模型的输出就不再取决于输入(可能是因为bias那么大)
- 不取决于输入也就是说误差导数会变得很小,接近零的导数说明权重位于一个权重空间的一处高原上,而很多人会误以为此时达到了局部最优点,就急匆匆地终止了训练。
损失函数的倾向性
- 分类任务中,如果用squared error或cross entropy error作为损失函数,输出单元会倾向于做如下不痛不痒的猜测:总是输出训练数据中标签=1的频率(即一直在学习截距,而没有在学习权重)。
- 如果学习速率过小,则神经网络要很长时间才能学习到有用的权重。
- 从结果上来看,error一开始下降很快(bias学习期),但是之后很长一段时间都没有多少改变(weight学习期),也会让人误以为达到了局部最优。
2.7 四种加速梯度下降的方法
- 使用”动量法“,详见下一届
- 每一处权重更新都有独立自适应学习速率
- RMSProp(根据梯度大小自适应的调整学习速率)
- 借助曲率信息优化迭代过程(详见后续课程)
3 动量法
The momentum method
3.1 动量法的直观理解

- 把初始化后的权重想象成误差曲线上的一个对应坐标的小球
- 小球在梯度的推动下脱离静止状态,开始沿着梯度方向移动
- 一旦小球具备了速度,小球接下来的运动方向将不再严格按照梯度方向移动
- 这是因为动量的作用,使得小球保持了一部分之前运动方向的倾向;如果不存在动量作用,由于红点与绿点的梯度几乎完全相反,小球将会出现在两点之间震荡的情况
- 而动量的存在,很好的抵消了这种高曲率方向上的震荡趋势,并且指向谷底方向的速度会被逐渐累积,最终使得小球能平滑而快速的达到最低点
3.2 动量法的公式推导
$$\begin{align} \Delta w(t) = v(t)&=\alpha v(t-1)-\epsilon \frac{\partial{E}}{\partial{w}}(t) \ \\ &=\alpha \Delta w(t-1)-\epsilon \frac{\partial{E}}{\partial{w}}(t) \end{align}$$
权重的改变量$\Delta w(t)$等价于当前时刻的速度$v(t)$ 当前时刻的速度$v(t)$取决于上一刻的速度$v(t-1)$和梯度$\frac{\partial{E}}{\partial{w}}(t)$ 其中$\alpha$表示衰减率,又被称为动量因子,$\epsilon$表示学习速率
假设误差曲面为一个倾斜的平面,并且动量因子$\alpha$接近于1 $$v(\infty)=\frac{1}{1-\alpha} \left(-\epsilon\frac{\partial{E}}{\partial{w}}\right) $$
- 随着时间的推移,最终的速度将会很大,刹车失灵警告!
- 所以大梯度配上高动量因子,很容易出现交通事故,此时建议调小动量因子,如取值$\alpha=0.5$
- 同理,当梯度变化较小(比如卡在某个峡谷的时候),也可以考虑逐渐增大动量因子进行脱困(如取值$\alpha=0.9$甚至$0.99$)
- 由于动量法可以减少震荡情况的出现,适当调高学习速率也值得一试
3.3 优化的动量法
标准的动量法是先计算当前位置的梯度,然后在累计的方向上前进一大步。
Ilya Sutskever 在2012年提出了一种优化版本(Nesterov动量法):
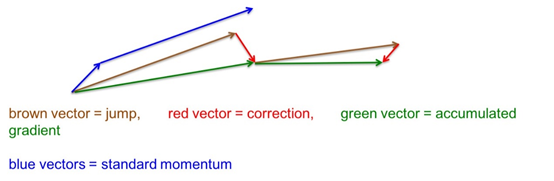
- 蓝线表示标准的动量法,绿线表示优化的动量法
- 标准的动量法是先计算梯度,再计算速度,最后更新权重
- 优化的动量法是先根据当前速度更新权重得到临时点(jump更新)
- 再根据临时点计算临时梯度(correctction更新)
- 最后用于实际速度和权重的更新(accumulated更新)
- ccumulated = jump + correctction
4 独立自适应学习速率
A separate, adaptive learning rate for each connection
4.1 独立自适应学习速率的直观理解
- 在多层神经网络中,不同权重的最优学习速率是多样化的
- 不同层之间的梯度量级可能会存在差异,尤其是在权重初始值偏小的时候
- 神经元输入量级较大时候,权重的细微改变就可能引起模型的巨大变化
- 可以考虑手动设定一个全局的学习速率,并根据局部的权重量级进行自适应调整
4.2 独立自适应学习速率的设计方案
- 为每一处连接的学习速率,设定单独的学习速率系数$g_{ij}$
- 权重的更新公式修正如下
$$\Delta w_{ij}=-\epsilon g_{ij}\frac{\partial{E}}{\partial{w_{ij}}}$$ 3. 当更新权重的梯度符号不变时,增大$g_{ij}$;反之则减少$g_{ij}$ 4. 具体更新$g_{ij}$的时候,增大用加法,减少用乘法: $$if\quad \left( \frac{\partial{E}}{\partial{w_{ij}}}(t) \frac{\partial{E}}{\partial{w_{ij}}}(t-1) \right)>0$$ $$then \quad g_{ij}(t)=g_{ij}(t-1)+.05$$ $$else \quad g_{ij}(t)=g_{ij}(t-1)\times .95$$ 4. 指数级的递减确保了在权重更新出现震荡时,$g_{ij}$能快速下降
有趣的结论
- 假设每一刻的梯度值都完全随机的
- 增大用加法:$g(t)=g(t-1)+\delta$,减少用乘法:$g(t)=g(t-1)\times (1-\delta)$
- 最终的$g_{i,j}$将会围绕
1上下波动
4.3 独立自适应学习速率的改进
- 限制$g_{ij}$在某一个合理区间内,如:$[0.1,10]\quad or\quad [0.01,100]$
- 样本过少的mini-batch会因为采样误差导致梯度符号变化无常
- 独立自适应学习速率可以和动量法可以综合使用
- 独立自适应学习速率只能在轴对齐的情况下起作用(?待理解)
5 rmsprop:考虑近期梯度的累积
rmsprop: Divide the gradient by a running average of its recent magnitude
5.1 只考虑梯度符号的rprop
- 不同权值之间的量级可能存在差异,这也是一个全局学习速率难以顾全的原因
- 在全量梯度下降算法中,可以考虑值只使用梯度的符号来进行更新,刺头直接削掉,杀伐果断~
- 只使用梯度的符号可以保证所有权重的更新都在一个量级,也能快速从一些梯度过小的“局部地区”逃离出来
- rprop方法就融汇了”只使用梯度的符号“和”独立学习速率“的想法
rprop方法概述
- 梯度符号前后一致时,则增大$g_{ij}$,如:$g(t)=g(t-1)\times 1.2$
- 梯度符号前后不一致时,则减小$g_{ij}$,如:$g(t)=g(t-1)\times 0.5$
- 控制每次更新的步长在一个特定的范围,如:百万分之一到五十之间
- 权重更新时只考虑梯度的符号,梯度通过除以历史梯度均值消除量级
rprop方法不适用于mini-batches
- 随机梯度下降法所产生的梯度相当于连续的小批次梯度的平均
- 比如说前九次的梯度为+0.1,而第十次的梯度为-0.9
- 在此情况下,最终的权重其实是基本不变的(梯度有效平均了)
- 而如果只考虑梯度的符号,并进行权重更新,则最终的权重会增加
思考:是否存在一种方法同时满足
- rmsprop的稳定性
- mini-batch的高效性
- 不同mini-batch之间的梯度有效平均
5.2 rmsprop:适用于mini-batch的rprop
- rprop是通过梯度除以均值的方式,去除了梯度的量级。
- 而mini-batch因为不同批次之间均值差异太大,可能会因此打破不同batch之间的梯度有效平均
- 解决方案:考虑临近批次使用近似的值进行梯度的标准化
rmsprop的思路就是维护一个滑动平均的值来保证临近批次的梯度有效平均 $$MeanSquare(w,t)=0.9\times MeanSquare(w,t-1)+ 0.1\times \left( \frac{\partial{E}}{\partial{w(t)}}\right)^2$$ 而rmsprop的梯度的标准化方法如下: $$stard(\frac{\partial{E}}{\partial{w(t)}})= \frac{\partial{E}}{\partial{w(t)}\sqrt{MeanSquare(w,t)}}$$
rmsprop与其他改进方法的结合:
- 动量法并不能帮助到rmsprop方法,具体原因待研究
- 优化版的动量法(Nesterov)可以进一步优化rmsprop,尤其是当梯度的标准化用在Nesterov动量法的correction部分时
- rmsprop能否结合独立自适应学习速率也是待研究的方向
- 其他的改进方向,Yann LeCun的研究组曾提出了”No more pesky learning rate“的研究成果
神经网络学习方法的总结
- 对于小规模数据(比如说小于1w)或更大但是信息冗余不足的数据,适合使用全量梯度下降法
- 对于大规模或者存在信息冗余的数据,适合使用小批次梯度下降法(同时是也可以结合诸如动量法或者其他改进方案,比如LeCun提出的那个)
- 一招鲜吃遍天的事情是痴心妄想,因为不同的神经网络存在明显差异,学习目标也琳琅满目,做人还是要踏踏实实的呀(ChatGPT:啊对对对)
更多梯度下降方法可参阅:梯度下降法族
参考
Hinton神经网络公开课6 Optimization: How to make the learning go faster