1 线性神经元的权值学习
Learning the weights of a linear neuron
1.1 感知器局限性
为什么感知机算法不能用于训练隐藏层
- 感知机算法的迭代目标是使得权值向量接近margin限制下的“最优”向量集合
- 如果两个权重向量是可行的,那么夹在它们中间的那些向量一定也可行,所以感知器算法处理的是一个convex问题。而在复杂网络中,两个可行的权值向量的平均可能并不可行(非凸)
- 所以严格来说,称呼神经网络为multi-layer perceptrons(多层感知机)是不对的。
转换一下视角
- 对于感知器来说,两个好的模型权重加和后可能还是好的
- 但是对于一些非凸问题来说可能就行不通了
- 不应该追求接近最优解的权重 而是追求预测结果更接近真实值
1.2 线性神经元
$$y=\sum_iW_ix_i=w^Tx$$ 其中$x$表示输入向量,$y$表示神经元输出向量,即输入向量的加权求和
神经元的优化目的是最小化真实值与预测值的均方误差
为什么不用解析法
- 上述问题可以通过解析法直接求解 $w=(x^Tx)^{-1}x^T\hat{y}$
- 科学家视角:人体的神经元不会矩阵运算~
- 工程师视角:尝试一种适用于多层非线性神经网络的解法
1.3 迭代法的简单示例
假设你每天都去餐厅吃固定的三种东西,但每次要的量不同,你也不会单价,只会一起付钱,那么你如何知道单价呢?
答案1:看一眼餐单 $\times$
答案2:积累数据建模迭代计算 $\checkmark$
$$price = x_{fish}w_{fish}+x_{chips}w_{chips}+x_{ketchup}w_{ketchup}$$
$$w=(w_{fish},w_{chips},w_{ketchup})$$
迭代法的一次完整计算过程:
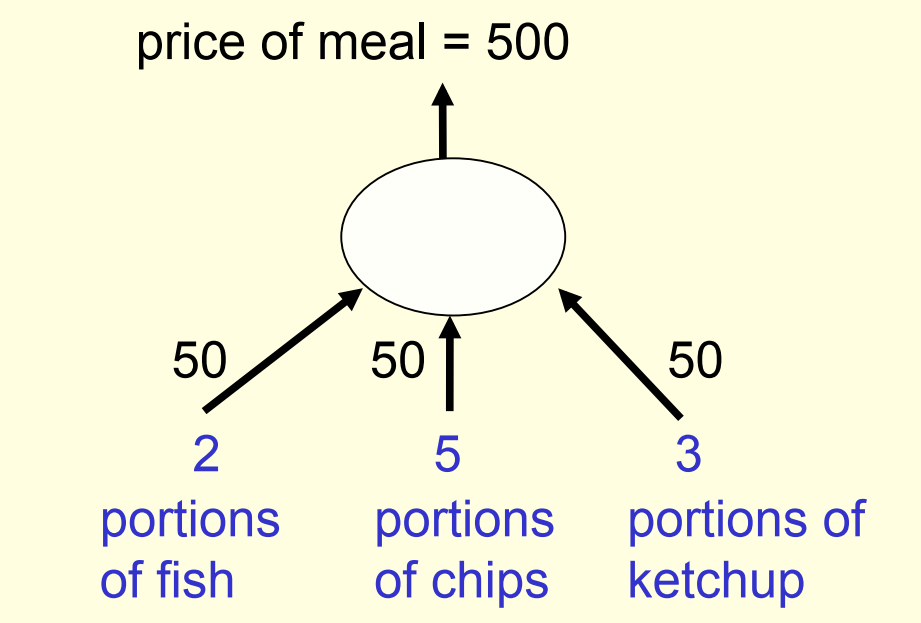
- 初始化权重矩阵为$[50, 50, 50]$
- 随机选择一个样本的输入特征$[2, 5, 3]$
- 经过线性神经元得到目标预测值target=500
- 实际消费为850,则预测误差error=350
- 根据德尔塔定律(
delta-rule)更新权重
$$\Delta w_i=\epsilon x_i(t-y)$$
- 设学习速率$\epsilon$=$\frac{1}{35}$,并根据公式对权重进行更新
- 更新后的权重矩阵为$[70, 100, 80]$
2 迭代法分析
是否一定有最优解? 可能没有最优解 通过调低学习速率,可以得到满足精度的近似解
迭代法的收敛速度? 输入特征的维度存在高度相关时,会导致收敛变慢。 你每次都只点一杯饮料、一个汉堡,还让人区分二者的单价!为难神经元呢!
与感知器求解算法的比较 迭代法每次都更新权重,感知器算法只在犯错时更新 迭代法存在参数-学习速率需要调整,还是无参最省心
3 线性神经元的误差曲面分析
The error surface for a linear neuron
3.1 误差曲面
基本定义:
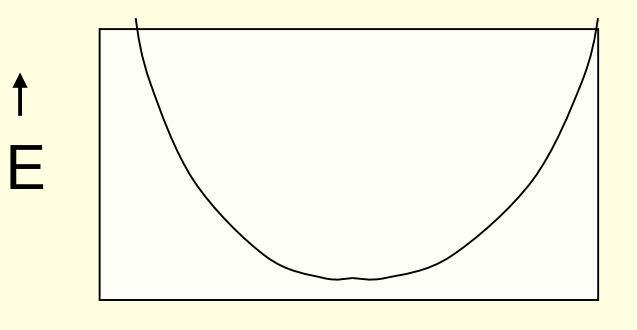
- 以权重的每个维度为x轴,误差项E为y轴,可以绘制误差曲面
- 在权重空间,对于每个维度做截面,都可以得到一个误差曲面
- 二维的误差曲面,如下图所式:
- 而对于更高维的权重空间来说,误差曲面将会复杂很多
3.2 基于误差曲面的分析
在线学习(Online learning) VS 批量学习(batch learning):
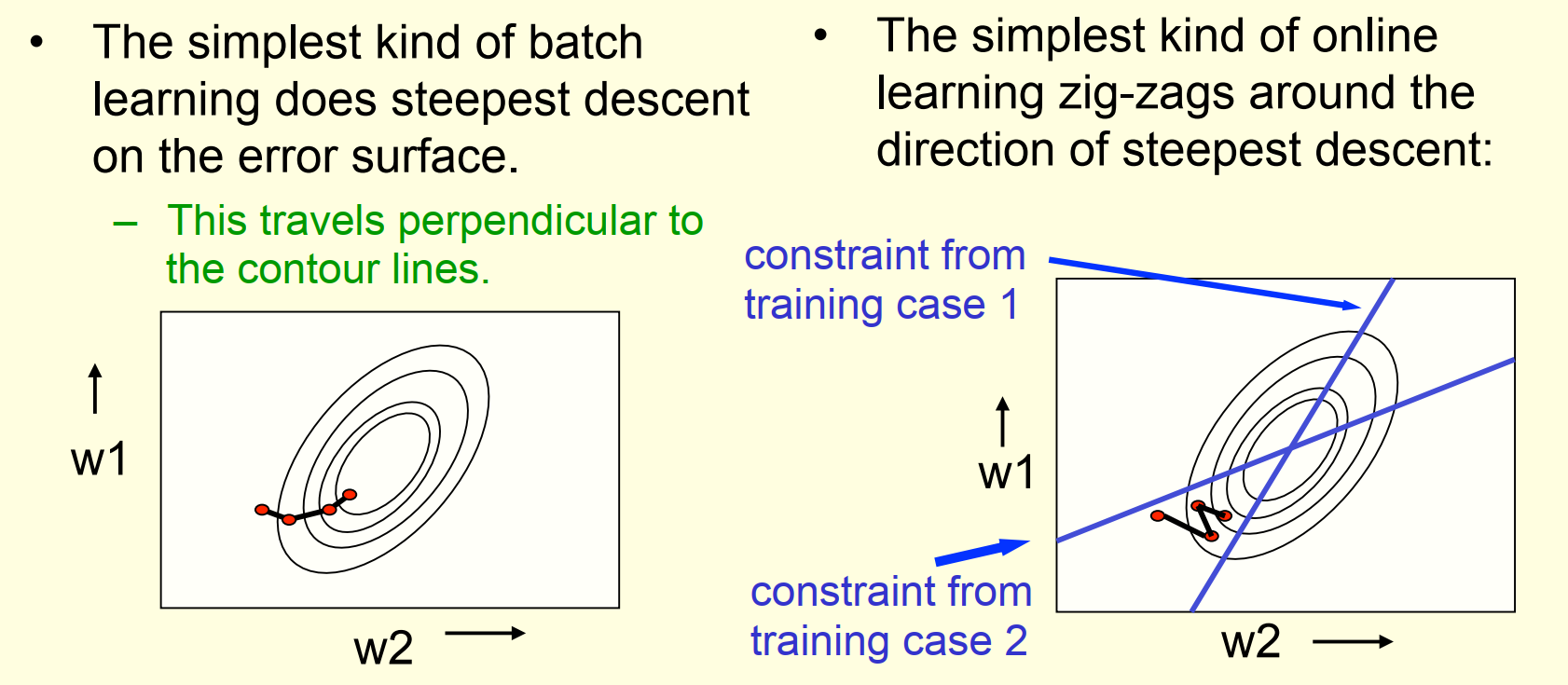
- batch learning 是按照梯度的方向走
- 梯度垂直于误差曲面构成的等高线
- online learning 是跟着单样本的梯度进行更新
- 权重会随着迭代沿着z字形路线逼近最优解
为什么学习速率会很慢
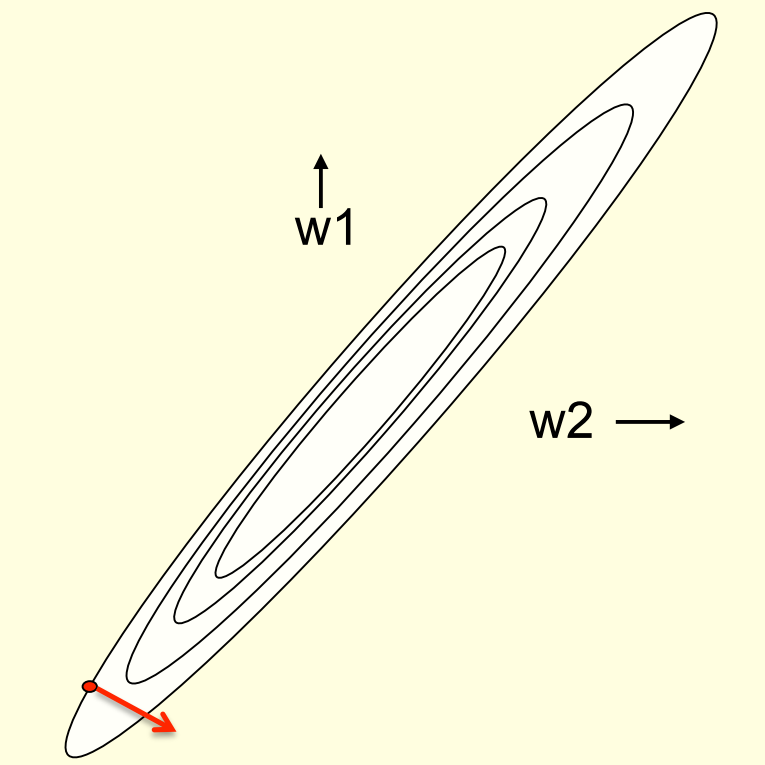
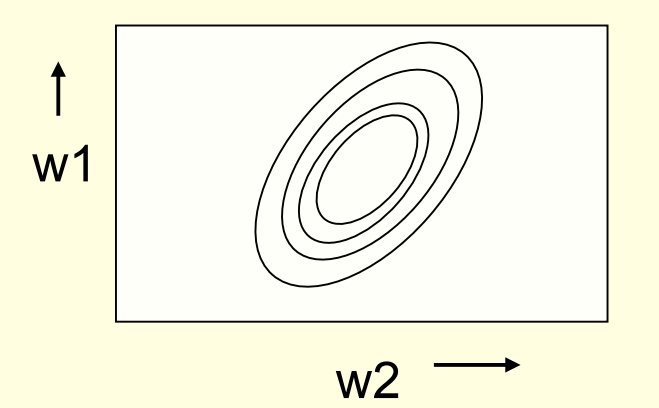
- 如果两个特征维度强相关,也就是它们的权重几乎相等,那么这两个维度的权值几乎落在y=x这条线的附近,进而构成如上图的椭圆形状
- 此时如果我们从红点出发,会发现红点的梯度指向与最优解方向几乎垂直。其在最优解方向上的分量是非常小的,所以收敛速度非常慢。
4 Logistic神经元的参数学习
Learning the weights of a logistic output neuron
从线性神经元到非线性神经元
4.1 sigmoid函数求导
Logistic 神经元也就是 sigmoid 神经元
其良好的求导特性让模型的学习更容易一些
4.2 Logistic神经元求导
已知 y 进行 z 求导结果如下 (证明见 sigmoid 神经元求导): $$ \begin{align} \frac{dy}{dz} = y(1-y) \end{align}$$
而根据链式法则可得: $$ \begin{align} \frac{\partial{y}}{\partial{w_i}}& = \frac{\partial{z}}{\partial{w_i}}\frac{\mathrm{d}y}{\mathrm{d}z} \ \\ & = x_iy(1-y) \end{align} $$
而损失函数$E=\frac{1}{2} \sum_{n\in traing}(t_n-y_n)^2$
再根据链式法则可得:
$$ \begin{align}
\frac{\partial{E}}{\partial{w_i}}& = \frac{\partial{y^n}}{\partial{w_i}}\frac{\partial{E}}{\partial{y^n}}
\ \\
& = \sum_nx_i^ny^n(1-y^n)(t^n-y^n)
\end{align}
$$
从另一个角度看
- $x_i^ny^n(1-y^n)(t^n-y^n)$可以拆成两个部分
- $x_i^n(t^n-y^n)$与感知器的
delta-rule一致- $y^n(1-y^n)$则是sigmoid函数引入的梯度
5 反向传播算法解析(一)
The backpropagation algorithm
5.1 再谈隐藏层
- 没有隐藏层的神经网络在输入和输出之间的映射能力偏弱
- 类似感知器的神经网络只有输入设计优秀的特征才能取得较好的效果
- 而我们期望的则是一种优秀特征的自动构建
5.2 通过随机扰动学习权重
随机扰动机制
- 随机改变某个权重的值
- 如果模型表现提升则保留改变
- 否则放弃,并进入下一次随机扰动
随机扰动机制的特点
- 符合强化学习的模式
- 非常低效,费力不讨好(大概也不容易收敛)
- 在学习的后期,较大的扰动很容易导致模型变差
5.3 改进的随机扰动
同时扰动所有权重?
- 最终效率依然非常低下
- 虽然权重的更新效率提高了
- 但是批量的权重更新可能混杂了好的更新和坏的更新
- 而为了区分这些更新的好坏,模型需要进行海量的批量更新去确定
随机干扰隐藏层的激活值?
- 隐藏层的数量远少于权重的数量
- 一旦知道了隐藏层的激活值是应该放大还是缩小
- 就可以相应的调整权重,以实现激活值的改进
- 不错的想法,但还是不如接下来要介绍的反向传播
5.4 反向传播算法的思考
反向传播背后的思想(以下内容是在老师的引导下的个人总结)
- 现有的神经网络网络不能直接指导权重的更新
- 但神经网络很容易计算出权重的更新对于损失函数的影响
- 每个隐藏层的激活值都会影响到输出层,进而干扰到预测值
- 反过来预测值和真实值的误差也可以指导激活值的更新
- 而借助链式法则,激活值的更新也可以传导到隐藏层参数的更新
5.5 反向传播算法简单示例(Sketch)
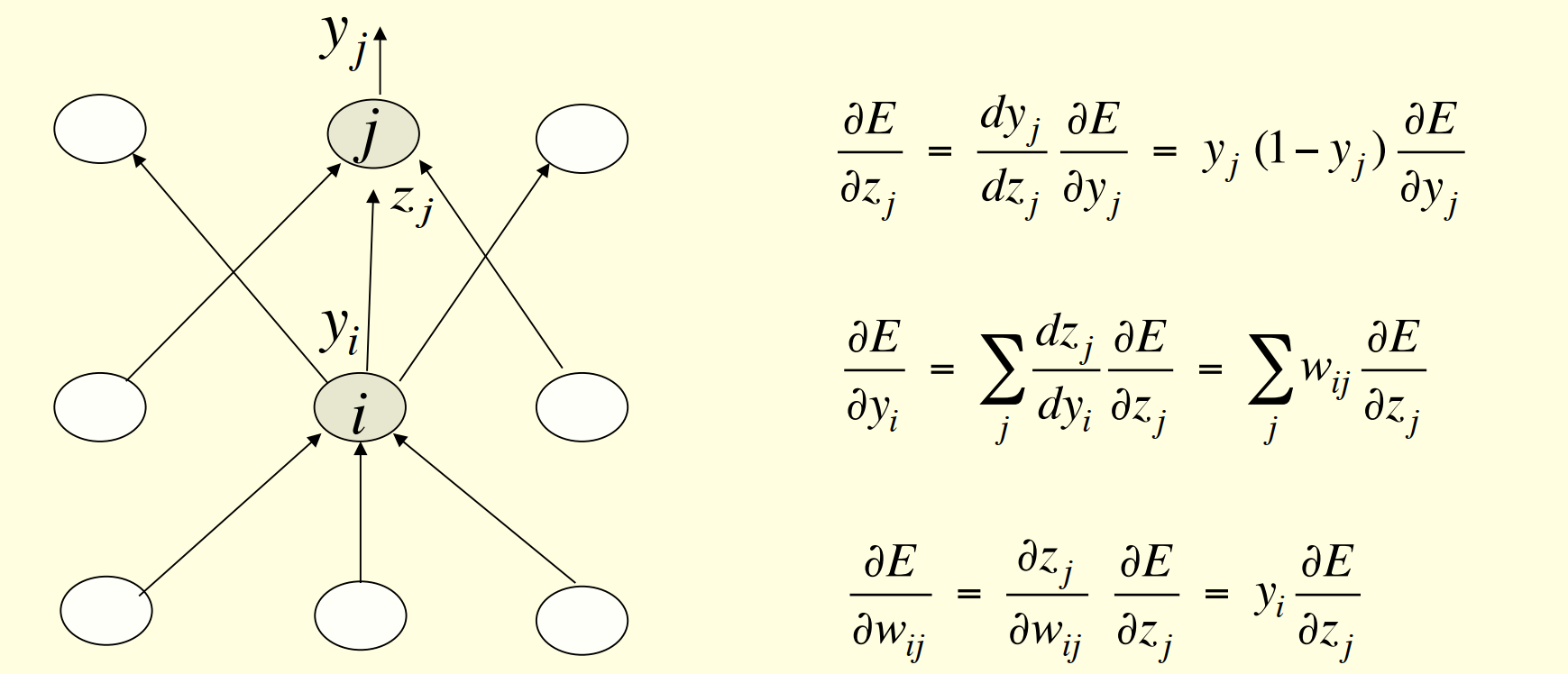
- 其中$E$表示损失函数$E=\frac{1}{2} \sum_{n\in traing}(t_n-y_n)^2$
- $y_j$表示输出层神经元$j$的输出,而$y_i$表示隐藏层神经元$i$的输出
- $z_j$表示隐藏层到输出层神经元$j$的加权求和结果
- $w_{ij}$表示神经元$i$到神经元$j$的权重
反向传播过程就是通过偏导和链式法则,得到损失函数与权重之间的导数关系,进而通过预测值和真实值的误差指导权重进行更新
6 反向传播算法的应用
How to use the derivatives computed by the backpropagation algorithm
反向传播算法以极为高效的方式实现了$\frac{dE}{dw}$的导数计算
但是在实际学习过程中,还是需要考虑两个重要的问题
下面就这两个问题进行简单概述
6.1 反向传播的优化问题
哪种更新权重的方式更合理?
- Online:单样本更新权重
- Full batch:全样本更新权重
- Mini batch:小批量样本更新权重
每次更新的步长多少合适?
- 固定学习速率?
- 自适应的全局学习速率?
- 每处神经网络连接分别自适应学习速率?
- 最速下降法合适吗?
6.2 泛化问题:过拟合
数据本身可能存在标记错误或采样误差
而一个强大的模型可能会拟合到这种误差,进而导致模型的真实表现稀烂
一个过拟合的示例
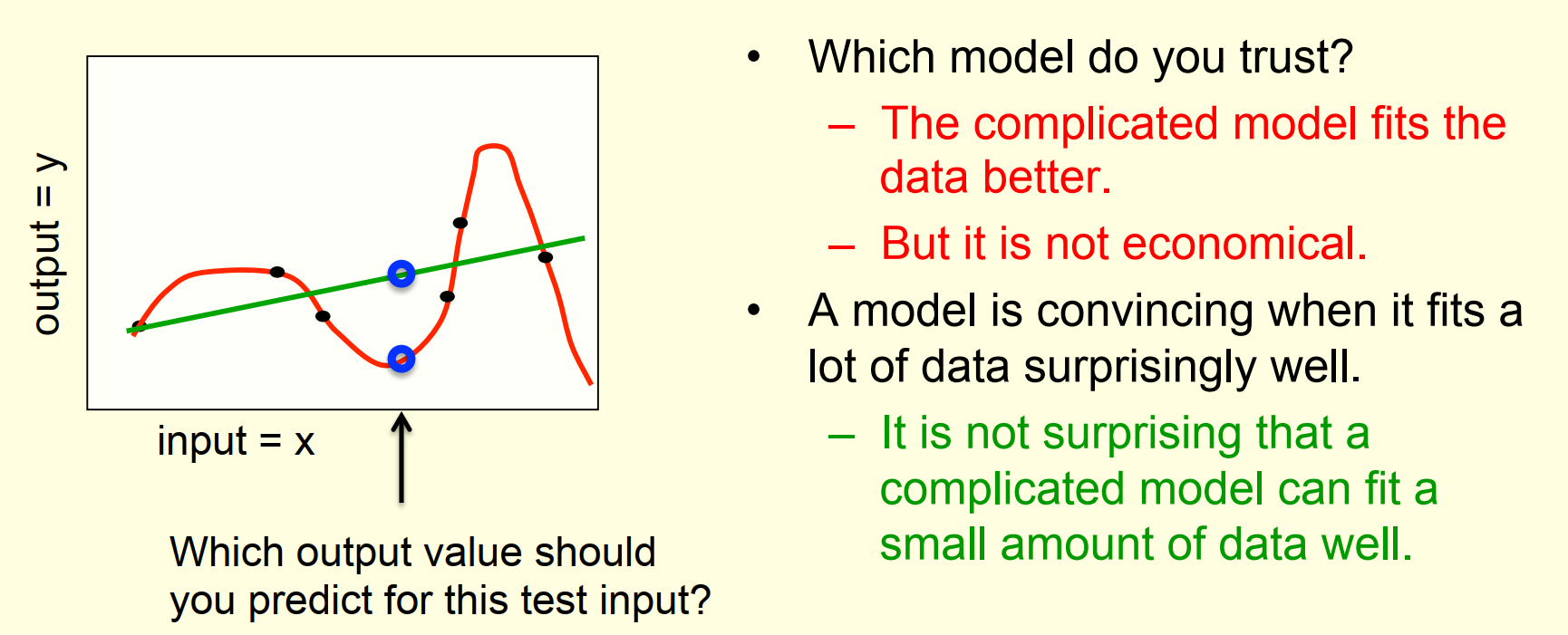
- 红线拟合的很完美,但过于复杂,不经济实用
- 根据奥卡姆剃刀原理,绿线是更优的选择
- 复杂模型面对小样本数据很容易出现过拟合的问题
几种减少过拟合的方法
- Weight-decay 权重衰减,相当于模型部分裁剪
- Weight-sharing 权重共享,相当于权重空间降维
- Early stopping 在验证集上表现开始变坏就终止训练
- Model averaging 对同一个数据集上训练的不同模型融合(取平均)
- Bayesian fitting of neural nets 另一种基于贝叶斯的模型融合
- Dropout 随机关闭部分隐藏层神经元,相当于模型部分拆分训练
- Generative pre-training 生成式模型预训练