1 序列建模概述
Modeling sequences: A brief overview
1.1 序列建模
- 将输入序列转化为另一领域的输出序列
- 比如语音识别就是将语音序列转化为文本序列
- 具备时序性的序列，可以将下一时序作为预测输出
- 比如股价预测或者文本生成，预测下一刻的价格或下文的用词
- 这种时序数据的建模，模糊了监督学习和非监督学习之间的边界
1.2 无记忆性的序列建模
自回归模型：
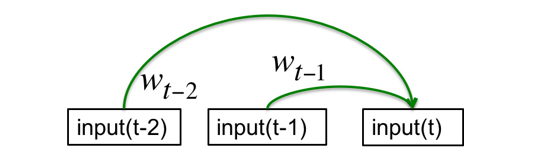
- 以序列T的第t项之前的n项为输入
- 通过线性回归建模，预测第t项
前向神经网络：
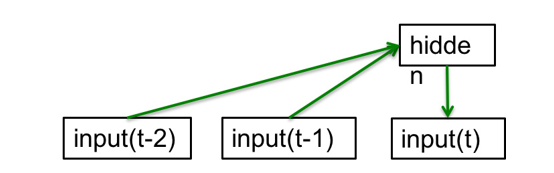
- 以序列T的第t项之前的n项为输入
- 通过神经网络构建隐藏层，并预测第t项
1.3 无记忆模型改进
引入隐藏状态改进无记忆模型
- 隐藏状态可以实现信息在迭代过程中的保留
- 如果迭代过程充满噪音，则隐藏状态也将是充满噪音而未知的
- 只能粗略推断出隐藏状态向量在空间上的概率分布情况
目前有两种模型是容易实现隐藏状态向量推断的
- Linear Dynamical Systems
- Hidden Markov Models
Linear Dynamical Systems(engineers love them!)
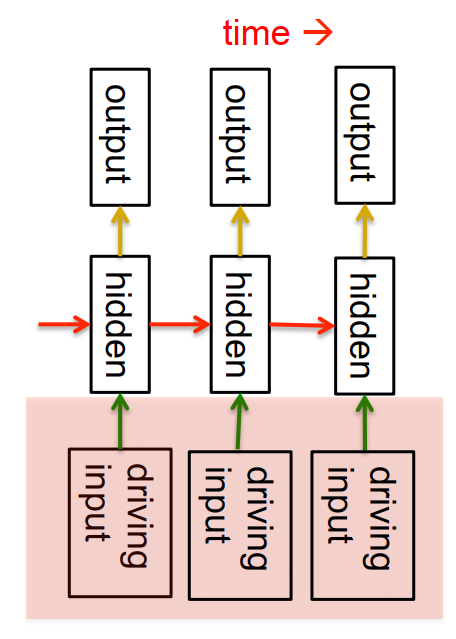
- 隐藏层由上一轮隐藏层和本轮输入决定
- 输出层和隐藏层之间通过线性模型关联
- 通常假设隐状态含有高斯噪音会取得较好的预测效果，比如导弹拦截系统
- （Linear Dynamical相关资料太少，细节 #待补充 ）
隐马尔科夫模型 Hidden Markov Models (computer scientists love them!)
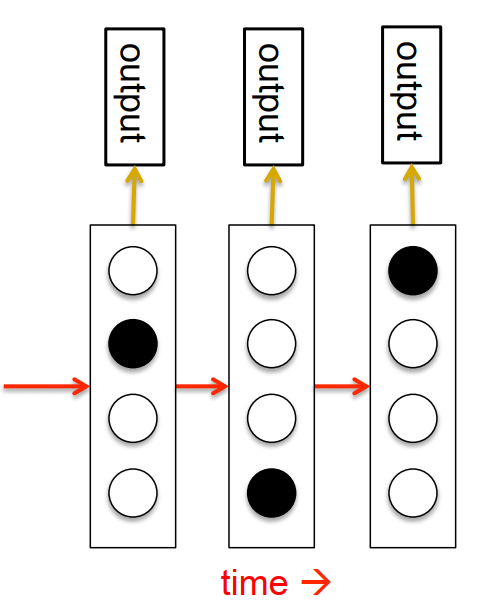
- 一般包含$1\times N$的离散隐藏状态
- 状态的转移是是随机的，概率由状态转移矩阵决定
- HMM很简单，整个系统只需要三个概率分布就能表示。而且通过动态规划，学习和预测都非常高效。
HMM的缺点：
- 离散的隐藏状态，所能包含的信息太少
- 对于复杂问题（如语音生成），需要考虑太多信息（语法、语义、语调、语速等等），最终所构建的隐藏状态也将非常高维
- 有点类似于用one-hot去强行建立所有词的向量矩阵~（巧合的是，RNN的隐藏层，相比于HMM的离散隐藏状态矩阵，具备了类似于word2vev和one-hot之间信息稠密化的特性）
更多细节可参阅：[[1_study/algorithm/概率图类模型/隐马尔可夫模型 HMM]]
1.4 循环神经网络
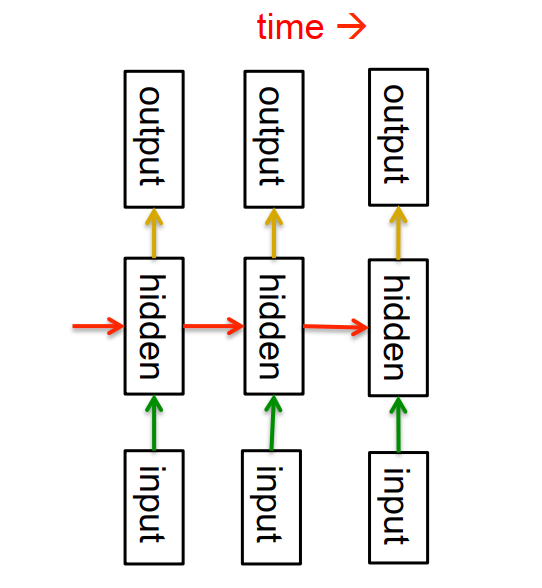
- 分布式的隐藏状态（隐藏层）确保了更多信息的高效存储
- 非线性的动态循环，使得隐藏层能捕捉到更复杂的信息
- 受限于动态循环的计算形式，RNN不能用矩阵计算加速（每个循环的计算，都依赖于对前一次循环的计算结果），因此相比于其他模型来说，计算成本高很多
思考：生成式模型一定需要是随机的吗？
- Linear dynamical systems和HMM是随机的，但给定观测数据，它们的隐状态后验概率分布其实是个确定性的函数
- RNN是确定式的，但RNN的隐藏状态完全可以看作是Linear dynamical systems和HMM中隐藏状态的确定性概率分布（所以RNN从能力上来说，相当于堆砌的多层HMM？）
2 用反向传播训练RNN
Training RNNs with backpropagation
2.1 RNN的反向传播算法思路
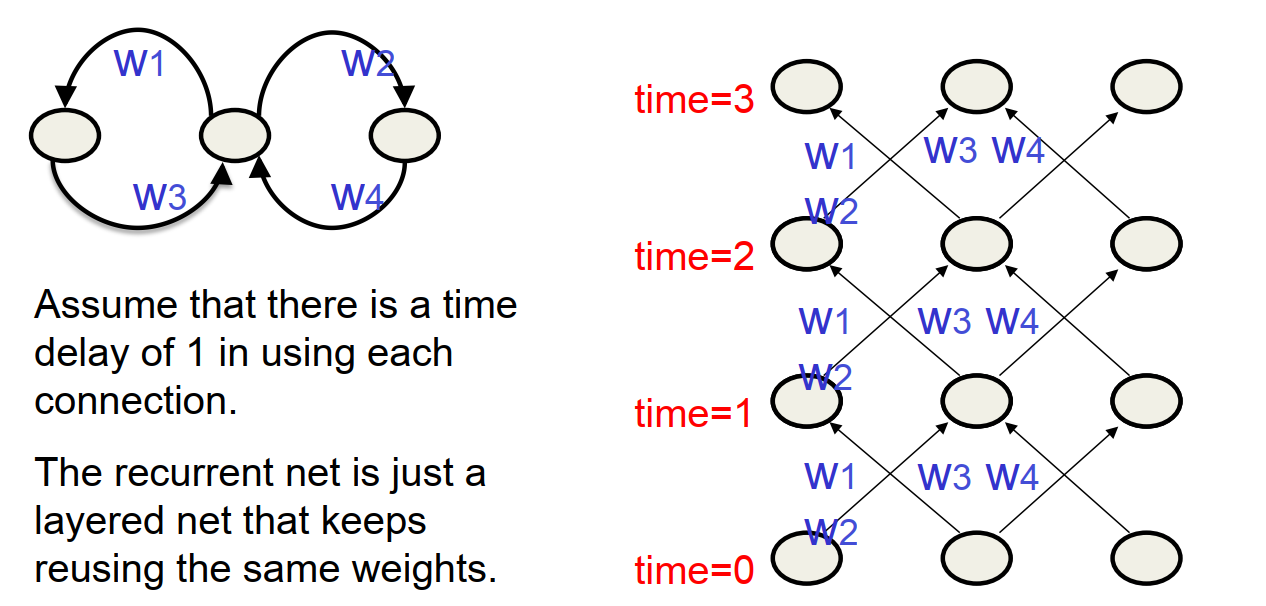
- RNN中的循环部分，可以从时域的角度展开，转变成普通的多层神经网络
- 循环部分展开的多层神经网络应该是权重共享的，中间值以栈的格式存储
- 前向传播在每次循环中产生一个激活值，将其压栈。反向传播将其出栈，然后计算误差。最后将所有误差导数分别求和并进行权重更新即可。
注意点
- 所有隐藏层和输出层的初始隐藏状态需要指定（可以直接先固定为0.5，但最好看作一个可学习的参数进行初始化）
- 隐藏状态向量的学习和权重的训练方法是一致的（随机初始化，根据误差计算梯度，以负梯度更新隐藏状态向量）
2.2 RNN的输入初始化方式
- 初始化所有输入单元的隐藏状态
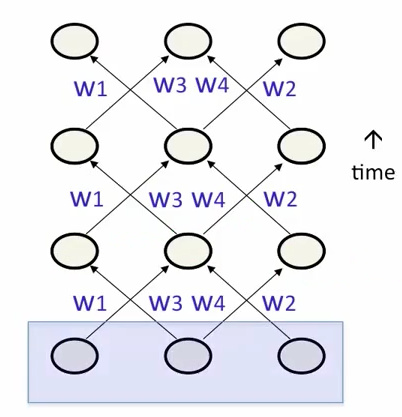
- 初始化部分输入单元的隐藏状态
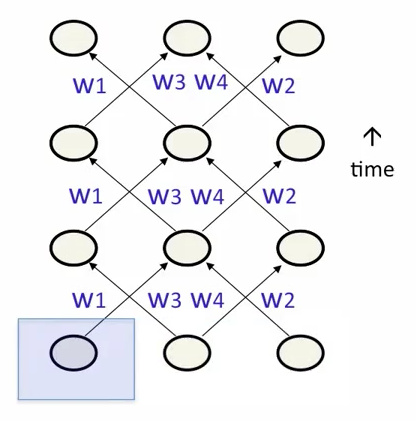
- 初始化每次循环的部分输入单元的隐藏状态（最推荐）
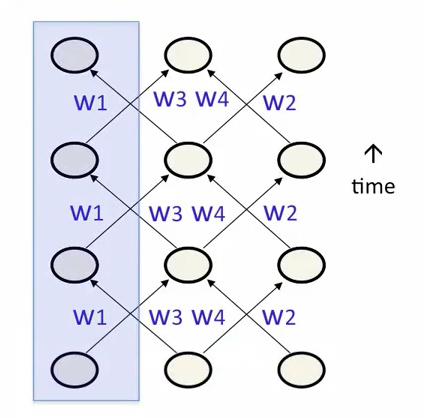
2.3 RNN的输出目标值设定
- 指定为所有输出单元的最终激活值
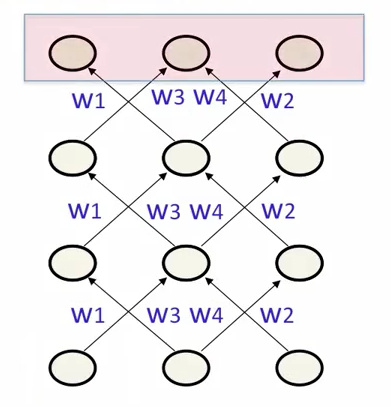
- 指定最后几次循环的所有输出单元的最终激活值
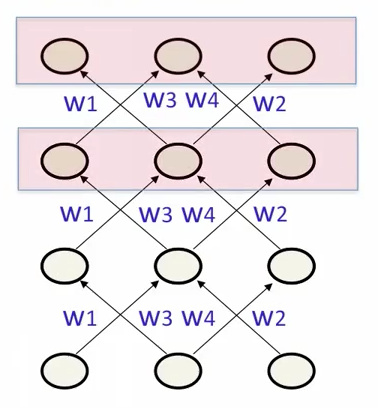
- 有利于学习长期行为
- 反向传播时更容易计算误差导数
- 指定部分单元（除输入元和隐藏元外的单元）的最终激活值
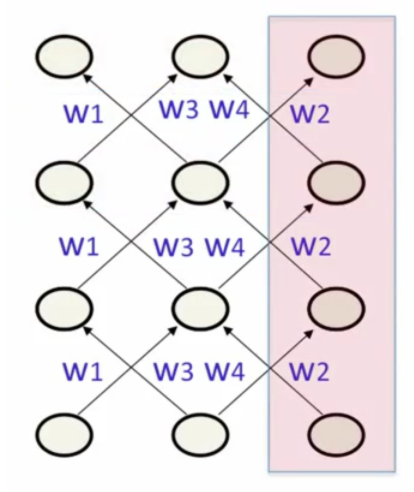
3 RNN的简单示例
A toy example of training an RNN
3.1 二进制加法建模分析
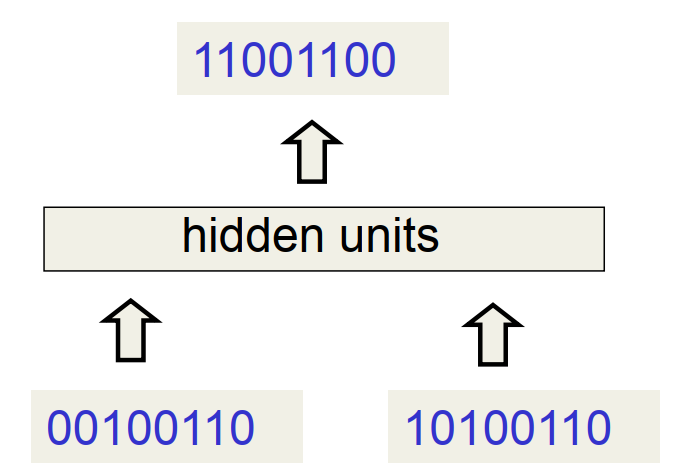
普通前馈神经网络无法很好地建模此问题
- 模型必须事先确定输入和输出的数字长度
- 无法满足加法互换法则，因为前后权重不一致
3.2 有限元自动机
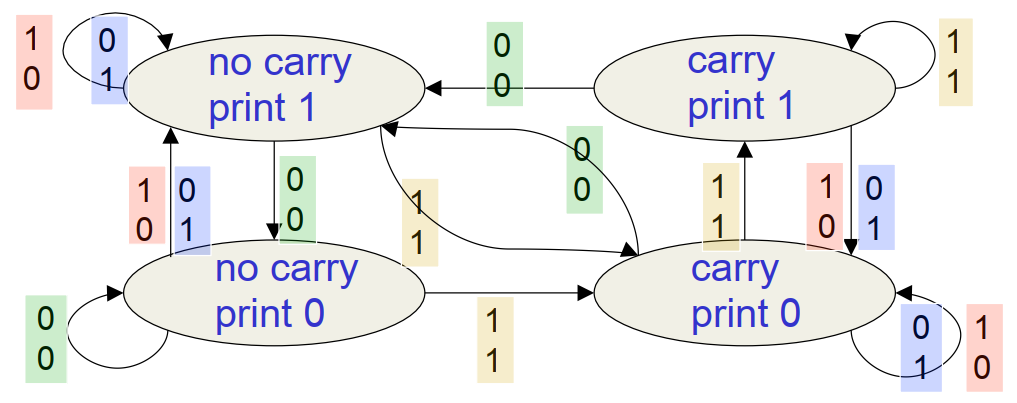上图为解决二进制加法的常见算法-有限元自动机
在本案例中它共有四个状态（这里的状态类似于HMM，不过并不是隐藏的）
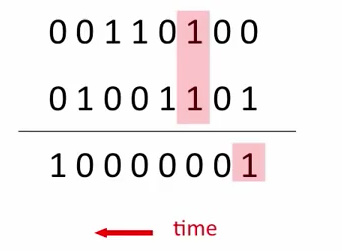
3.3 RNN加法建模
RNN每次循环包括两个输入神经元和一个输出神经元
网络结构中间层包含三个隐藏神经元
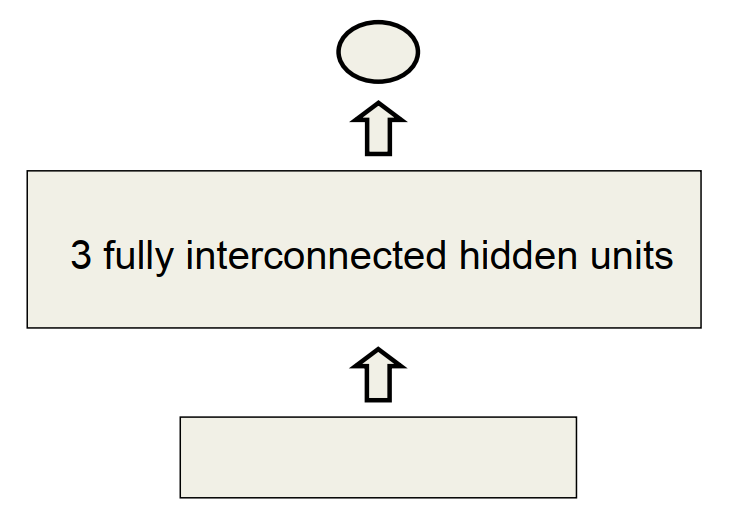
- 三个隐藏神经元之间是相互连接的
- 确保前一次循环保留的隐含特征能传递到下一次循环
网络的学习效果
- 三个隐藏神经元学到了四种模式（与自动机正好对应）
- 神经网络中的神经元与自动机中的节点是不同的，神经元是一个可学习的状态向量，而节点只是用于标识状态的0-1矩阵。
- 自动机只能处于一个状态，而隐藏神经元则被限制为一个向量。
- RNN可以模拟有限状态自动机，但前者明显更强大。
- 对于一个包含N个隐藏神经元的RNN来说，只需要$N^2$个参数就能表示$2^N$种布尔型状态。
- 如果输入信息翻倍，则无限元自动机所需要的状态数目将指数级增长，而RNN只需将隐藏神经元翻倍。
4 RNN训练的难点
Why it is difficult to train an RNN
4.1 前向与后向传播的差别
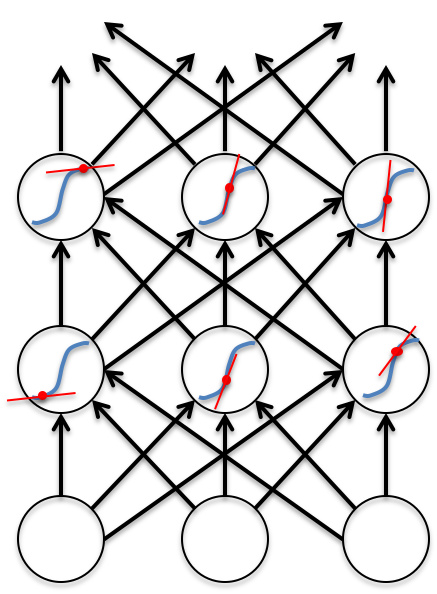
- 前向传播需要通过一些squashing function（比如sigmoid函数）限制激活值的过快膨胀（exploding）
- 后向传播则是完全线性的（squashing function的导数一般都是线性的），也就是说误差扩大两倍，相应的误差导数也会扩大两倍
- 而从函数图像上考虑，反向传播计算时所利用的偏导其实就是正向传播时激活函数所对应的函数图像（蓝色曲线）在激活值（红色圆点）处的斜率（红色直线）
- 反向传播的线性特征，将容易导致误差/梯度在多层传递逐渐趋近于0（梯度消失）或趋近于$\infty$（梯度爆炸）
4.2 梯度爆炸与梯度消失
- 不同层之间的反向传播是线性的，所以如果每层偏导系数很小的话，则梯度会指数级减小，即梯度消失；反之则会指数级增长，也就是梯度爆炸
- 这种问题在浅层类神经网络中不常见，但很容易出现在基于长序列（比如100个时间单位）训练的RNN中
- 合理的初始化权值能一定程度上预防这个问题，但还是很难让长序列的早期信息得到保留并输出，也就是说模型缺乏长记忆性
4.3 RNN的四种改进方式
- Long Short Term Memory：通过特定的神经元设计让RNN具备长记忆性
- Hessian Free Optimization：通过设计一个可以根据微小梯度或者曲率来识别方向的优化器（HF optimizer），来避免梯度消失的问题
- Echo State Networks：对所有权重更谨慎地初始化（确保产生出足够表征特征的隐藏状态），并只对隐藏层到输出层之间的连接进行权重更新
- Good initialization with momentum：以ESN的方式进行权重初始化，并采用动量法的方式对所有权重进行更新
5 长短期记忆网络LSTM
Long term short term memory
5.1 LSTM模型
- 由Hochreiter 和 Schmidhuber 在1997年提出，用于改进RNN，使其具备长记忆（记住几百次循环之前的信息）能力
- 新增的记忆单元是logistic神经元和线性神经元的乘法组合
- 记忆单元包含write、keep和read这三种门，分别用于控制信息的写入，存储和读取。
记忆单元结构：
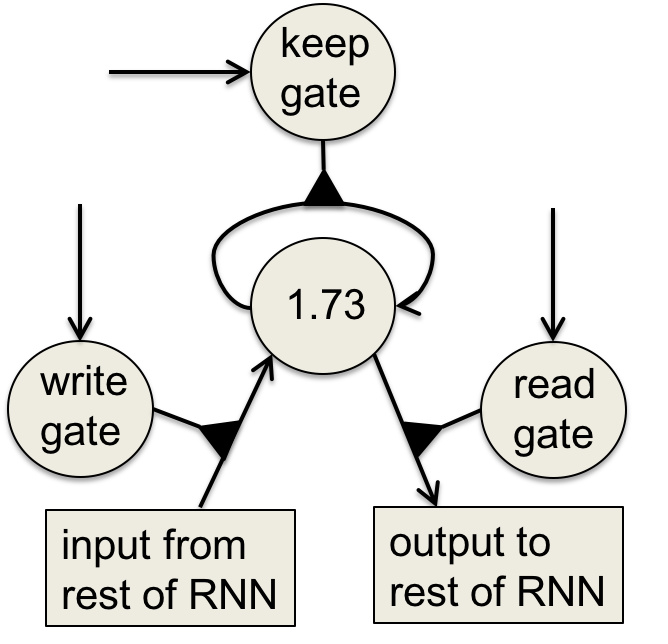
- 整体结构采用类似于电路的方式模拟信息的存储
- 中间的线性神经元通过keep门保持权重为1的自连接来存储信息
- 激活write门将会产生信息的覆盖，而激活read门将会导致信息的输出
- 三个门的激活状态是通过logistics函数实现的，具有友好的导数性质
5.2 LSTM的反向传播
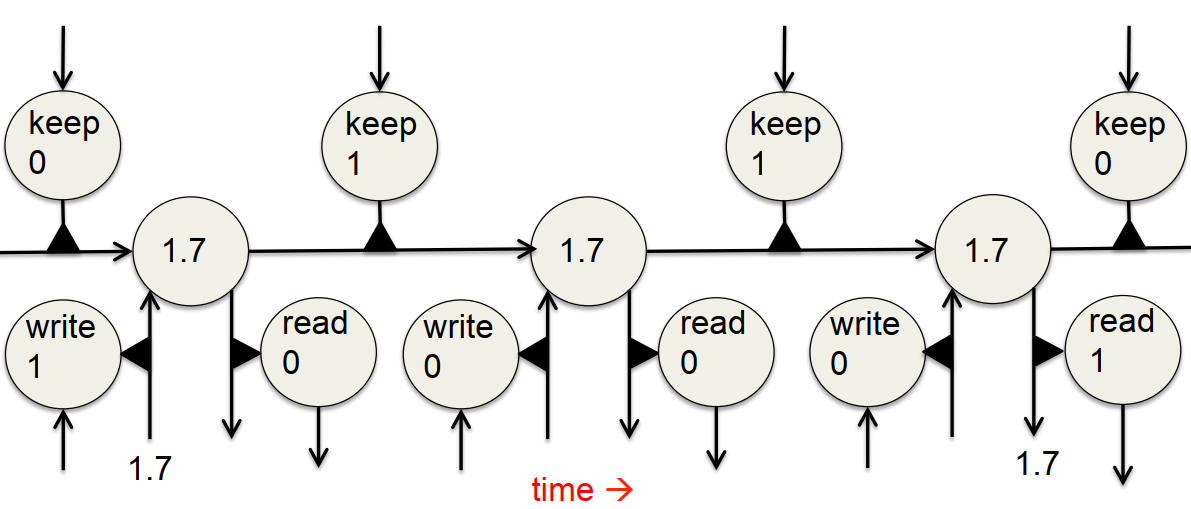
- 前向传播容易理解，上图由左到右，充分体现了LSTM对信息的记忆、保持、读取，并在最终遗忘的过程
- 状态的递归梯度可以看作为1，这样就能保持状态不随着误差的反向传播而更新（这一结论在LSTM的原始论文中是成立的，因为当时对梯度进行了截断）
课外补充：完整的递归梯度计算下的LSTM
- 状态更新函数中的加法特性，使得导数值可以在1上下跳动
- 门函数赋予网络决定梯度消失程度得能力，如果长期依赖对结果有重要影响，网络会把遗忘门值设置得更大，从而缓解梯度消失问题；反之则会调低遗忘门值，而这都是通过网络学习来自动调节的
- 具体可参考为什么LSTM可以阻止梯度消失：从反向传播视角来考虑（博客翻译）
5.3 LSTM应用：手写字识别
- 输入值是形式为（x,y,p）的连续坐标，构成笔迹轨迹，其中p表示笔是否落下
- 输出是模型识别并生成的对应字符
- Graves和Schmidhuber在2009年的工作表现出了LSTM对于此类任务的优越性（他们采用的输入是一连串的小图片）。
效果展示：
- 第一行表示识别出的字母，对于识别难度较高的字母将会延迟输出
- 第二行表示记忆单元部分子集的状态，可以注意到每当模型识别出字母时，状态将会重置
- 第三行表示输入的手写文本，一般来说图片输入往往要优于坐标输入
- 第四行表示反向传播过程中对于输入坐标的梯度强度，这能直观地表现出哪些信息在影响当前的模型决策