前置知识:1_study/math/马尔可夫模型
隐马尔可夫模型
可视马尔可夫模型的状态是可知的,而隐马尔可夫模型(The Hidden Markov Model,简称 HMM)的状态是不可知,但存在可知的序列观察值
以典型的看病模型为例,设病人的状态有两种:{健康(Healthy),发烧(Fever)}
医生不能直接知道病人的状态,但能够得知病人的健康状况:{正常(Normal),发寒(Cold), 头晕(Dizzy)},作为一个行医多年的鬼才医生,他可以构建出看病用的隐马尔可夫模型:
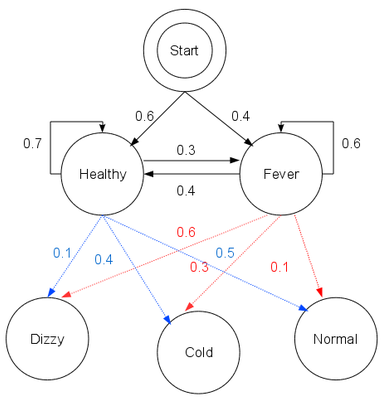
注:HMM其实是朴素贝叶斯的序列标注版
HMM的求解思路
借助隐马尔可夫模型,可以解决以下 3 类问题:
- 评估(Evaluation)
- 定义:给定 HMM,求观察值的可能概率
- 举例:一个病人第一天头晕,求第二天头晕的概率
- 解决方法:暴力枚举、前向算法、后向算法
- 解码(Decoding)
- 定义:给定 HMM 和观察值,求状态的可能性
- 举例:一个病人第一天头晕,第二天发寒,求他这两天的健康状况
- 解决方法:1_study/algorithm/动态规划算法/维特比算法 Viterbi#3 维特比算法示例
- 学习(Learning)
- 定义:给定观察值序列,求解 HMM 的参数
- 举例:根据医生最近一年的看病记录,判断头晕病人发烧概率、第二天继续头晕的概率、第二天康复的概率(确定初始状态分布与状态转移概率矩阵)
- 解决方法:Baum-Welch 算法(不存在大量标注数据),极大似然估计或其他有监督学习算法(存在大量标注数据)
鲍姆-韦尔奇算法(Baum-Welch)
- 采用1_study/algorithm/迭代优化算法/期望最大化 EM 算法的原理,不过该算法的出现早于 EM 算法
- 假设当前的可观测序列为 $O$,当前不可观测状态为 $I$,当前模型参数为 $\overline{\lambda}$
- E 步:基于条件概率 $P(I|O,\overline{\lambda})$ 计算联合分布 $P(O,I|\lambda)$ 的期望表达式 $$
L(\lambda, \overline{\lambda}) = \sum\limits_{I}P(I|O,\overline{\lambda})logP(O,I|\lambda) $$
- M 步:根据期望表达式的最大化,得到更新后的模型参数 $\overline{\lambda}$ $$
\overline{\lambda} = arg;\max_{\lambda}\sum\limits_{I}P(I|O,\overline{\lambda})logP(O,I|\lambda) $$
- 通过不断的E步和M步的迭代,直到 $\overline{\lambda}$ 逐渐收敛
HMM 应用与进阶
具体应用:
进阶阅读:
高阶 HMM
- 初始的HMM是基于马尔可夫链来实现的,认为当前时刻的状态,只受前一时刻的影响
- 二阶马尔可夫链:当前时刻状态,只受前两个时刻的影响(以此可类推 N 阶马尔可夫链)
- 二阶马尔可夫链构建隐马尔可夫模型时,得到的就是二阶隐马尔可夫模型,简称2-HMM
层次化HMM
层次化隐马尔可夫模型(The Hierarchical Hidden Markov Model),简称HHMM
当序列过长时,HMM的复杂度会很高(指数级增长),因此提出了HHMM将HMM进行层次化的拆分,简单来说,就是原本状态与观察值的转换关系,变成了状态与观察值序列的转换关系。
 (摘自宗成庆的《统计自然语言处理》)
(摘自宗成庆的《统计自然语言处理》)
备注:为了方便理解上图,可以把$q^1$层看作初始化层,$q^2$层看作句子相关的特征,$q^3$层看作词语相关的特征,$q^4$层看作字相关的特征
参考
如何用简单易懂的例子解释隐马尔可夫模型? - henry的回答 - 知乎