1 马尔可夫随机场
一个无向图，结点表示随机变量，边表示两个随机变量之间的概率依赖关系，每个随机变量都可以指定一种可能取值，当变量满足马尔可夫性（即变量的可能取值只与它的临近变量有关）时，这时的图就叫马尔可夫网络，也就是马尔可夫随机场。（非严谨定义）
以构建以词性标注为例，假设一个句子由10个单词组成的句子，每个单词的词性选择有10种，则马尔可夫随机场就限制了所有单词的词性只和它前后的单词有关系。
2 条件随机场
条件随机场=马尔可夫随机场+条件概率
将马尔可夫随机场中的随机变量看作$y$，然后增加一个对应的观察值序列$X$后，给定$X$情况下的马尔可夫随机场就是条件随机场，简称CRF。
机器学习中CRF最常见的结构是链式结构（即不存在多个$y$之间互相依赖的情况）：
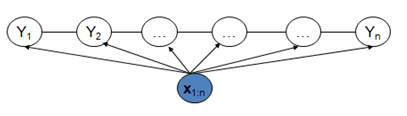
3 CRF 目标函数
设$x={x_1,x_2,...}$，而$y=y_1,y_2,...$
最终的状态序列概率为 $$P(Y=y|x)=\frac{1}{Z(x)}exp(\Sigma_k\lambda_k\Sigma_it_k(y_{i-1},y{i},x,i)+\Sigma_l\mu_l\Sigma_is_l(y_{i},x,i))$$ $$Z(x)=\Sigma_yexp(\Sigma_k\lambda_k\Sigma_it_k(y_{i-1},y{i},x,i)+\Sigma_l\mu_l\Sigma_is_l(y_{i},x,i))$$
- 其中$Z(x)$表示规范化因子；
- $t_k(y_{i-1},y{i},x,i)$表示转移特征，是定义在边上的特征函数，依赖于当前状态和前一刻状态，而$\lambda_k$是转移特征对应的权重；
- $s_l(y_{i},x,i)$表示状态特征，是定义在结点上的特征函数，依赖于当前状态，而$\mu_l$是状态特征对应的权重；
3.1 目标函数简化
把转移特征和状态特征合写为$F(y,x)$，相应权重合写为$w$，最终目标函数为： $$P(y|x)=\frac{1}{Z(x)}exp(w\times F(y,x))$$
3.2 特征函数举例
一般来说，特征函数的取值为 1 或 0 ，当满足规定条件时取值为 1 ，否则为 0。
以词性标注为例：
$s_1(y_i,x,i)=1$，该函数可以用于表示当单词是以-ly结尾的且$y_i=ADVERB$时，返回$1$，否则返回$0$，当$\lambda_1$较大时，模型将倾向于将以-ly结尾单词标注为副词
$t_1(y_{i-1},y_i,x,i)=1$，该函数可以用于表示当$y_{i-1}=ADJECTIVE$且$y_i=NOUN$时，返回$1$，否则返回$0$，当$\mu_1$较大时，模型将倾向于认为形容词后面常跟着名称
4 CRF常见应用
和[[1_study/algorithm/概率图类模型/隐马尔可夫模型 HMM#3 HMM的常见应用]]一样，CRF也包含评估（Evaluation）、解码（Decoding）、学习（Learning）这三种问题
前两个问题的解决方法是类似，评估问题需要通过前向或后向计算解决；解码问题需要使用维特比算法来求解；CRF的学习问题也很容易，因为存在目标函数，所以梯度下降法、牛顿迭代法什么的都可以用~
5 CRF VS HMM
- CRF能构建特征函数，更充分的利用观察值序列$X$
- CRF的最终结果是全局最优的，而HMM只是具备最优
- CRF是判别式模型，而HMM是生成式模型
- CRF更加依赖于特征函数的构建，训练成本高