一个典型的神经元

- Axon 轴突
- Dendritic tress 树突
- Axon hillock 轴突体
线性神经元
$$y = b+\sum_ix_iw_i$$

二进制阈值神经元
对线性加权运算的结果,进行阈值判定
$$z = b+\sum_ix_iw_i$$
$$\begin{equation}
y = \left\{
\begin{array}{rl}
1 & \mbox{if } z \geq 0, \\
0 & \mbox otherwise.
\end{array} \right.
\end{equation}$$

Relu 神经元
为函数引入了最简单的非线性部分 $$z = b+\sum_ix_iw_i$$ $$\begin{equation} y = \left\{ \begin{array}{rl} z & \mbox{if } z > 0, \\ 0 & \mbox otherwise. \end{array} \right. \end{equation}$$

Leaky Relu:x 的负半轴保持一个较低的斜率,接近 0 但不为0
sigmoid 神经元
特性优秀,求导简单多用于二分类模型结果的输出
$$z = b+\sum_ix_iw_i$$ $$y = \frac{1}{1+e^{-z}}$$
对 y 进行 z 求导结果如下: $$ \begin{align} \frac{dy}{dz} & = \frac{-1(-e^{-z})} {(1+e^{-z})^{2}} \ \\ & = y\frac{e^{-z}} {(1+e^{-z})} \ \\ & = y\frac{(e^{-z}+1)-1} {(1+e^{-z})} \ \\ & = y(1-y) \end{align}$$
而根据链式法则可得: $$ \begin{align} \frac{\partial{y}}{\partial{w_i}}& = \frac{\partial{z}}{\partial{w_i}}\frac{\mathrm{d}y}{\mathrm{d}z} \ \\ & = x_iy(1-y) \end{align} $$

缺点:
- 当 $z$ 过大或过小时,梯度接近 0(饱和现象),导致参数训练困难(梯度消失)
- 计算复杂度偏高(存在指数运算),输出结果非 0 均值
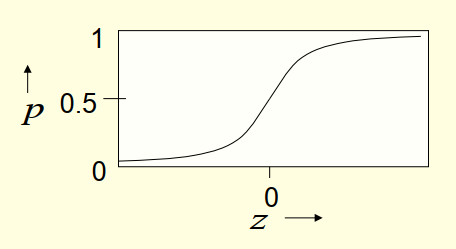
随机二进制神经元
逻辑单元和 sigmoid 一致,但是结果会作为概率进行随机取值 最终结果会是 0 或 1,只能说更大的正数会导致最终出现 1 的可能性变大
$$z = b+\sum_ix_iw_i$$
$$p(s=1) = \frac{1}{1+e^{-z}}$$
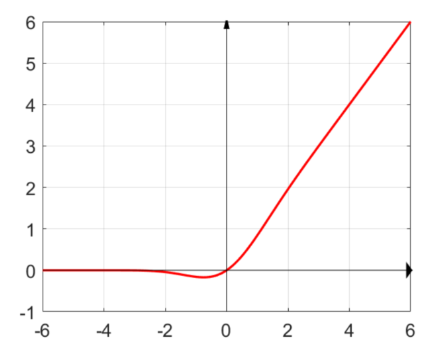
GELU 神经元
高斯误差线性神经元(Gaussian Error Linear Unit)
$$GELU(X)=x\times P(X\leq x)=x\times \Phi(x)$$
其中 $\Phi(x)$ 表示高斯正态分布的累积函数,所以上式可转化为:
$$x\times P(X\leq x)=x\int_{-\infty}^x\frac{e^{-\frac{(X-\mu)^2}{2\sigma^2}}}{\sqrt{2\pi}\sigma}dX$$
在实际应用中,可用以下公式进行近似表示:
$$GELU(x)=0.5x[1+tanh(\sqrt{\frac{2}{\pi}}(x+0.047715x^3))]$$