1 梯度下降法-简单版
大部分机器学习模型的构建都是寻找最小损失函数的过程,而梯度下降法(Gradient Descent)便是一种常见迭代优化算法,用于寻找损失最小的参数解。
以简单二次函数为例进行算法的简单说明,模型形式如下:$\hat{y}=f(x)=\theta_0+\theta_1x^2$
使用$RMSE$作为损失函数可表示为:$J(\theta_0,\theta_1)=\frac{1}{n}\Sigma_{i=1}^n(y_i-\hat{y}_i)^2$
模型的训练过程(参数的更新过程)可表示为: $$\begin{equation} \left\{ \begin{gathered} \theta_0=\theta_0-\alpha\frac{\partial{}}{\partial{\theta_0}}J(\theta_0,\theta_1) \ \\ \theta_1=\theta_1-\alpha\frac{\partial{}}{\partial{\theta_1}}J(\theta_0,\theta_1) \end{gathered} \right. \end{equation}$$ 当迭代次数达到最大或者参数基本不再变化时,算法运行结束
这就是梯度下降法的最简单实现,其中$\alpha$表示学习速率(learning rate)
2 梯度下降法-矩阵版
理解梯度:MIT18.02关于梯度的解释
实际情况下的梯度下降法,其核心思想与简单版的梯度下降法并无太大区别,主要是输入特征维度与参数量的增加。但相应地,公式最好也要以矩阵向量的形式进行展示。
假设模型表示为$f(x;\Theta)$,其中$x$表示输入向量,$\Theta$表示模型的参数集合;模型的损失函数为$L(f(x;\Theta),y)$;预设超参数$\alpha$表示学习速率
梯度下降法:
- 对模型参数$\Theta$进行初始化,随机选择$m$个样本${(x_1,y_1),...,(x_m,y_m)}$
- 计算$m$个样本的平均损失:$\Sigma_{i=1}^mL(f(x_i;\Theta),y_i)/m$
- 对参数进行更新$\Theta \leftarrow \Theta-\alpha\nabla_{\Theta} \Sigma_{i=1}^mL(f(x_i;\Theta),y_i)/m$
- 重复以上过程,直到迭代次数达到最大或参数基本收敛
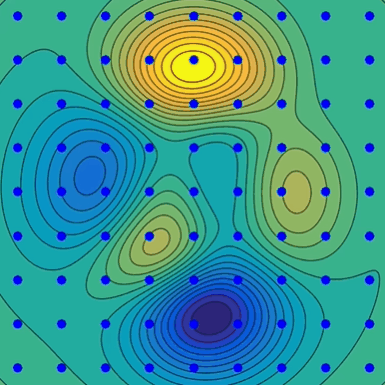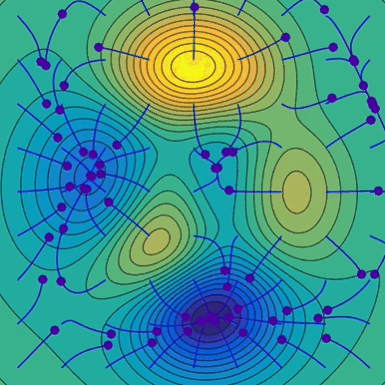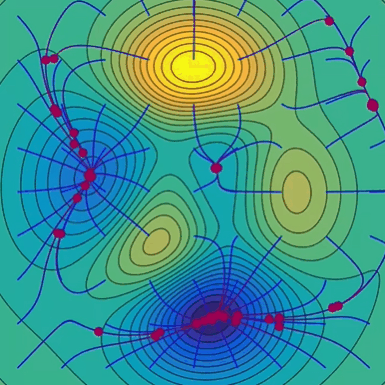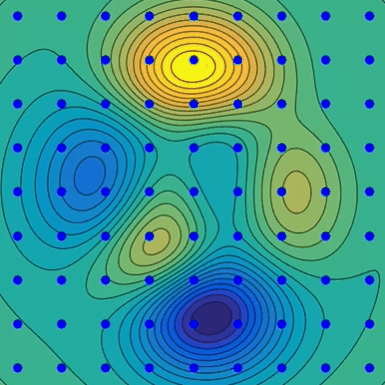
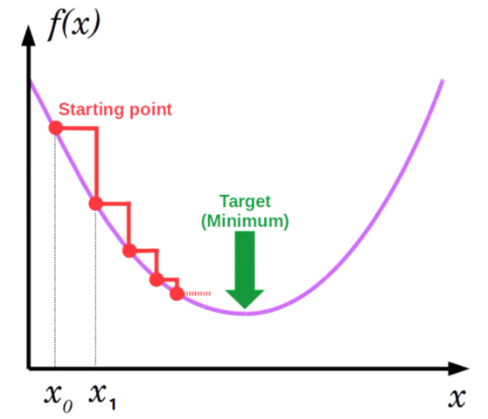
梯度下降的直观理解(下山问题):
梯度下降法分析:
- 对于最大化优化问题,可以对目标函数简单取一个负号转化为最小值优化问题
- 当损失函数是凸函数时,梯度下降法的解是全局最优解,否则可能是局部最优解
- 学习速率过小时,会影响模型的收敛速度;过大时,可能导致模型的无法稳定收敛
3 批次(Batch)梯度下降法
计算所有样本的损失均值,并通过反向传播更新参数
算法分析:收敛稳定,适合并行计算;数据量较多时,计算成本较高
4 随机(Stochastic )梯度下降法
计算单个样本的损失均值,并通过反向传播更新参数
算法分析:计算快,但是单样本的随机性导致收敛不稳定,不适合并行计算
5 小批次(mini-batch)梯度下降法
计算$m$个样本的损失均值,并通过反向传播更新参数
算法分析:融汇了全量梯度下降法和随机梯度下降法的优点,更值得信赖
6 带有动量(Momentum)的梯度下降法
动量法在进行参数更新时,会考虑历史的梯度值,使得梯度的下降过程产生一种“惯性”
假设当前的梯度值为$g$,历史的梯度值为$V$,则动量法的参数更新过程如下: $$\begin{equation} \left\{ \begin{gathered} V \leftarrow & \beta V+(1-\beta)g \ \\ \Theta \leftarrow & \Theta-\alpha V \end{gathered} \right. \end{equation}$$ 其中$\beta$表示动量参数(确保过去的梯度信息会指数级衰减),常取值为0.9
算法分析:
- 两种不同方向的动量可能会互相抵消,促使收敛速度加快,并缓解优化停滞的问题
- $\beta$的取值作为衰减指数决定了动量的影响持续性,比如$\beta=0.5$会仅考虑最近的几次惯性,$\beta=0.99$则大约会考虑最近的几十个梯度
其他资料补充:Hinton《机器学习与神经网络》-动量法
7 自适应梯度下降(AdaGrad)算法
AdaGrad算法会根据梯度的大小自适应的调整学习速率
假设当前的梯度值为$g$,历史累积的梯度值平方和为$r$,则AdaGrad算法更新过程如下: $$\begin{equation} \left\{ \begin{gathered} r \leftarrow & r+g\cdot g \ \\
\Theta \leftarrow & \Theta-\frac{\alpha}{\epsilon+\sqrt{r}} g
\end{gathered}
\right. \end{equation}$$ 其中$\epsilon$表示小常数,常取值为$10^{-6}$
算法分析:
- 当梯度较大时,修正的学习速率会显著减小
- 当梯度较小时,修正的学习速率不会产生显著变化
- AdaGrad算法很适合用对稀疏特征的情况
- 随着迭代次数的增加,AdaGrad算法的学习速率可能会是过低的
8 RMSProp算法
RMSProp算法在AdaGrad算法的基础上进行改进,限制学习速率的下降速度
RMSProp算法更新过程如下: $$\begin{equation} \left\{ \begin{gathered} r \leftarrow & \beta r+(1-\beta)g\cdot g \ \\
\Theta \leftarrow & \Theta-\frac{\alpha}{\sqrt{r+\epsilon}} g
\end{gathered}
\right. \end{equation}$$ 其中$\beta$为衰减系数,常取值为0.9
算法分析:引入衰减系数避免历史梯度值的累积导致学习速率过低
其他资料补充:Hinton《机器学习与神经网络》-动量法
9 AdaDelta算法
AdaDelta算法是对AdaGrad算法的另一种改进,调整了学习速率的修正逻辑
AdaDelta算法更新过程如下: $$\begin{equation} \left\{ \begin{gathered} r \leftarrow & \beta r+(1-\beta)g\cdot g \ \\
\Theta \leftarrow & \Theta-\frac{\sqrt{d+\epsilon}}{\sqrt{r+\epsilon}} g
\ \\\\
d \leftarrow & \beta d+(1-\beta)\Delta w^2
\end{gathered}
\right. \end{equation}$$ 算法分析:
- 将学习速率与参数的变化程度关联(广义上讲,AdaDelta算法是没有学习速率的)
- 在迭代初期,参数的变化较为剧烈,对应的学习速率更大
- 随着迭代次数的增加,参数的变化趋于平和,对应的学习速率也就越小
10 Adam算法
Adam(Adaptive Moment Estimation)算法吸收了AdaGrad算法(自适应学习率的梯度下降算法)和动量梯度下降算法的优点,既能适应稀疏梯度(常见于自然语言和计算机视觉问题),又能缓解梯度震荡的问题
Adam算法更新过程如下: $$\begin{equation} \left\{ \begin{gathered} r \leftarrow & \beta_1 r+(1-\beta_1)g \ \\ d \leftarrow & \beta_2 d+(1-\beta_2)g\cdot g \ \\ \Theta \leftarrow & \Theta-\frac{\alpha}{\sqrt{d/(1-\beta_1)}+\epsilon} r/(1-\beta_2) \end{gathered} \right. \end{equation}$$ 其中超参数常用值分别为:$\alpha=0.001,\beta_1=0.9,\beta_2=0.999,\epsilon=10^{-8}$
算法分析:
- 博采众长,实战效果优秀,可作为日常使用时的默认首选项
- 梯度差异过大可能影响到参数的收敛,可通过改进$d$的更新修正此问题
11 其他优化技巧
- 借助线搜索加速收敛:
- 每次计算梯度后,借助二分搜索寻找使损失下降最多的最优的学习速率
- 理论上此方法会极大提高收敛速度,但是线搜索的每一步都需要计算全局损失,对于神经网络等模型来说,全局损失的反复计算成本过高了
- 预热(warm up):
- 在迭代初期使用较小的学习速率更新模型
- 避免初始化的随机性影响模型的稳定性
- 一般来说,带有warm-up策略的学习速率会先增后减
- 学习率调度器:
- 制定个性化的策略对学习速率进行额外的调整
- 常见的单因子策略包括:多项式衰减、分段常数式衰减、乘法衰减
- 一般来说,策略中的学习速率都会随着迭代过程逐渐衰减(注意设定合理的下界)
- 余弦调度器:在迭代的后期使用很小的学习速率来慢慢地改进模型