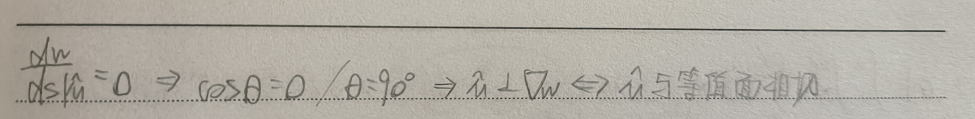1 梯度
回归上一节,对于函数$w(x,y,z)$,当$x=x(t),y=y(t),z=z(t)$时,求导可得: $$\frac{dw}{dt}=w_x\frac{dx}{dt}+w_y\frac{dy}{dt}+w_z\frac{dz}{dt}=\nabla_w\cdot \frac{d\vec{r}}{dt}$$
这里其实是一种将多元微分从乘加形式向点积形式的简化转换
其中$\nabla_w$表示梯度向量,为各方向偏导组成的向量: $$\nabla_w=<w_x,w_y,w_z>$$ 其中$\frac{d\vec{r}}{dt}$表示速度向量$\vec{v}$: $$\frac{d\vec{r}}{dt}=<\frac{dx}{dt},\frac{dy}{dt},\frac{dz}{dt}>$$ 例题:以$w=x^2+y^2$为例,对应的梯度为$<2x,2y>$
取任意的常数值$c$,令$x^2+y^2=c$可得函数$w$的等值面
梯度性质:梯度向量垂直于函数的等值线(面)
梯度性质拓展:梯度向量指向函数值增长最快的方向
2 梯度性质证明
当函数值$w=c$时,$\Delta w(t)=0$,即$\nabla_w \cdot \vec{v}=0$,所以$\nabla_w$与$\vec{v}$垂直
由于$\vec{v}$与等值面相切(这里是一种速度与轨迹间的相切关系)且$\vec{v}$是任意的
而所有的$\vec{v}$构成了切平面(确保结论在任意高维上,依然成立)
可得$\nabla_w$垂直于切平面,所以$\nabla_w$垂直于等值面
注意:这里的证明借助了线性近似的思想,用切平面代替等值面
例题:求解$x^2+y^2-z^2=4$在点$(2,1,1)$处的切平面
计算可得此点的梯度为$\nabla_w=<4,2,-2>$
根据梯度性质可得切平面为$4x+2y-2z=k$,带入点$(2,1,1)$
解得$k=8$,所以切平面方程为$4x+2y-2z=8$
3 方向导数
假设存在函数$w=w(x,y)$,其在$x$轴和$y$轴方向的方向导数为$\frac{\partial{w}}{\partial{x}},\frac{\partial{w}}{\partial{y}}$
思考:对于任意的向量$\vec{u}=<a,b>$,如何计算函数$w$在方向$\vec{u}$上的导数
解决:考虑链式发展,并进行x和y的扩展
- 引入变量$s$,并令$x(s)=x_0+as$,$y(s)=y_0+as$
- 将$x(s)$和$y(s)$带入函数$w$后求导,得到${\frac{dw}{ds}}_{|\vec{u}}$
- ${\frac{dw}{ds}}_{|\vec{u}}$即函数沿$\vec{u}$方向的导数
假设$\vec{u}$为单位向量: $${\frac{dw}{ds}}_{|\vec{u}}=\nabla_w\cdot \vec{u}=|\nabla_w|cos(\theta)$$
深入理解方向导数
- 当$\theta=0$时,$cos(\theta)=1$,此时$\vec{u}$与梯度方向平行,方向导数最大,说明对应的函数变化最大,所以梯度向量指向函数值增长最快的方向
- 当$\theta=90°$时,$cos(\theta)=0$,此时$\vec{u}$与梯度方向垂直,方向导数为0,函数值不再变化(对应等值面的定义),$\vec{u}$属于切平面,与等值面相切
4 参考