1 学会预测下一个词
Learning to predict the next word
1.1 关系信息
下图包含了家庭的关系信息，其中=表示夫妻关系：
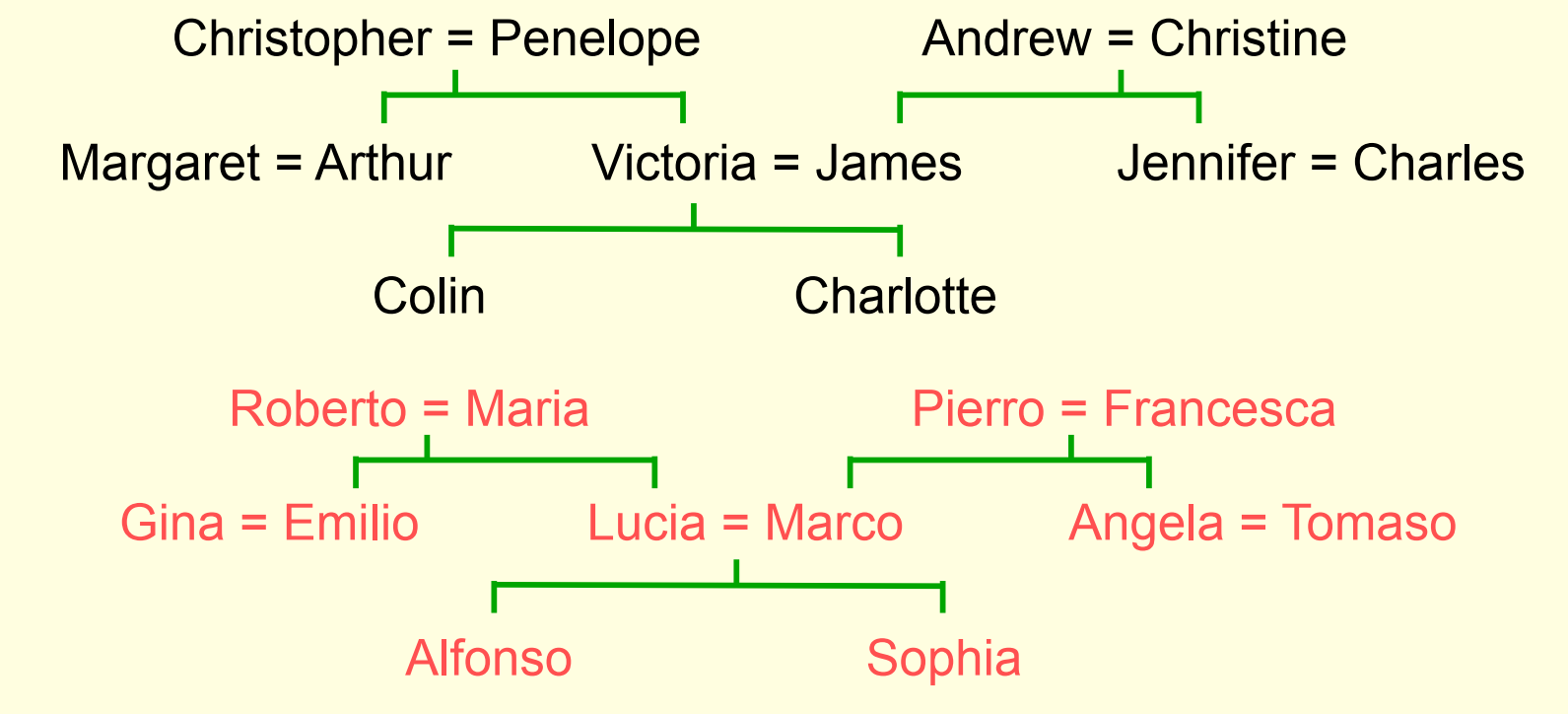
关系信息的表示方法
- 建立12种关系规则
- 上下关系8种（son, daughter, nephew, niece, father, mother, uncle, aunt）
- 平辈关系4种（brother, sister, husband, wife）
- 黑色表示一张英国人的家谱，而红色表示一张结构相似的意大利人的家谱
- 信息的表示方法举例：(colin has-father james)
- 信息存在推导关系：
思考：
- 给定大量的家庭关系三元组数据，神经网络能否学会其中的推导关系？
- 需要注意的是，这种规则是广泛存在于离散空间中的，而神经网络学会的规则会处于一种连续权重空间。（当然，用连续表征离散，我认为是可行的，最典型的莫过于word2vec中离散词的向量化）
1.2 神经网络结构
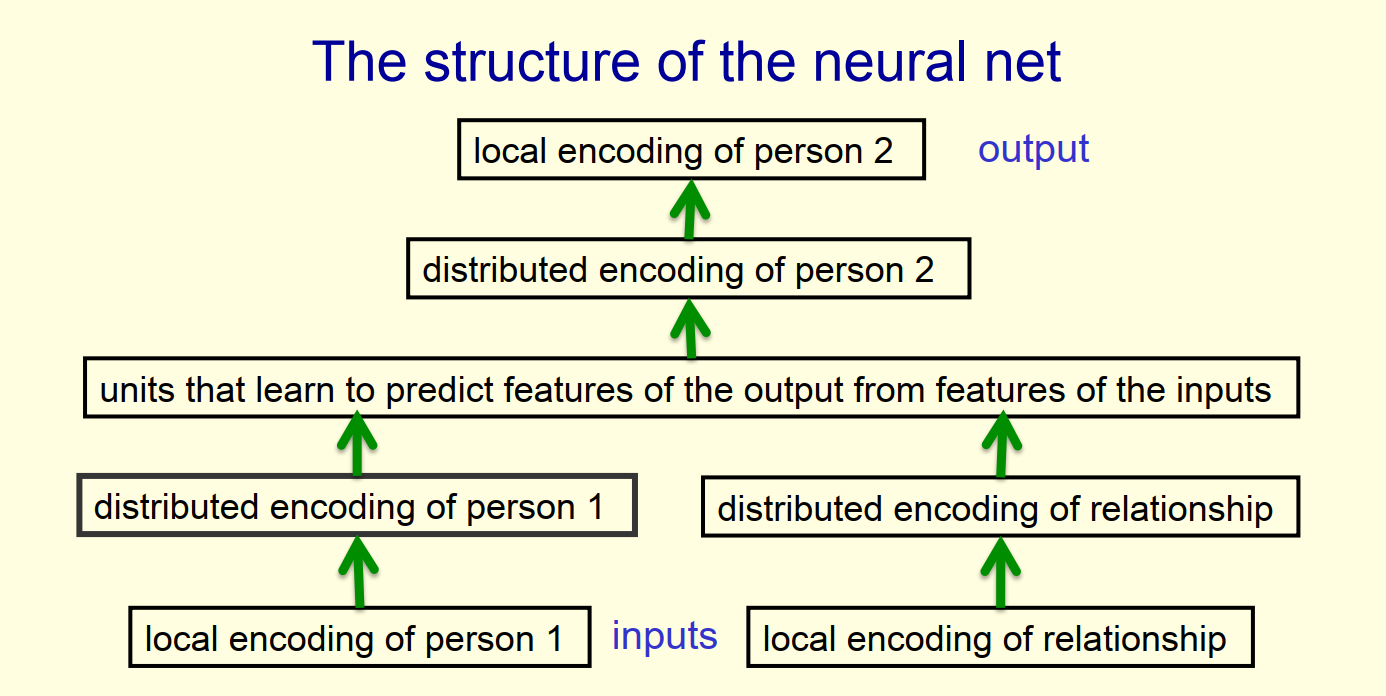
- 模型输入：包含person1和relationship两部分，二者都经过one-hot向量化处理，其中person1是$1\times24$的一维矩阵，而relationship是$1\times12$的一维矩阵
- 模型输出：是与person1之间满足relationship的person2，其中person2是$1\times24$的一维矩阵
- 输入输出举例：（大头儿子，父亲）=> 小头爸爸
- 从local encoding 到distributed encoding：这是一个高维稀疏矩阵转为低维稠密矩阵的降维过程，类似word2vec中的词向量化过程
- 中间隐藏层：实现基于relationship从peason1到peason2的推理
- 从distributed encoding 到 local encoding：这是一个低维稠密矩阵逆转为高维稀疏矩阵的过程，确定了最终peason2的预测值
1.3 神经网络的有效性
神经元可视化：
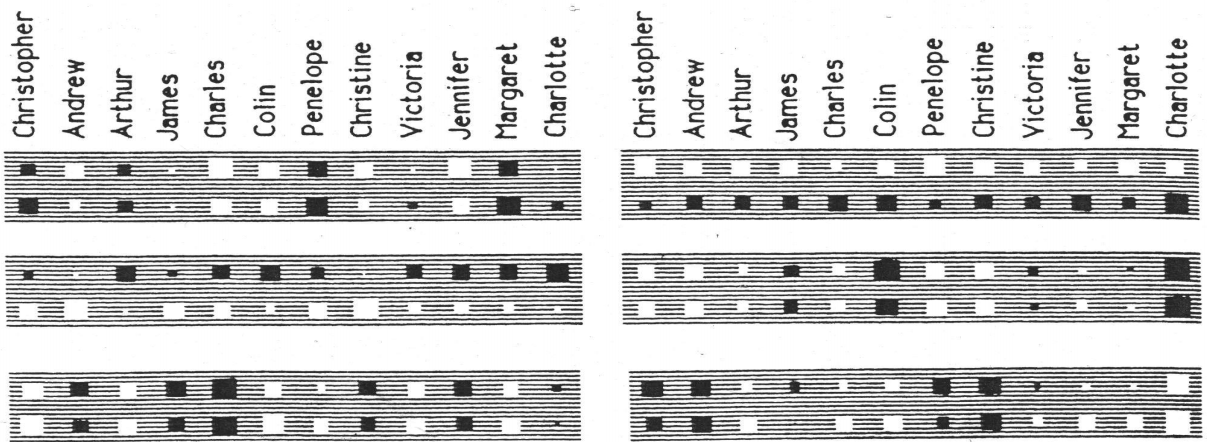
- 六个大长方形，对应6个神经元，负责将24维进行低维（6维）稠密表示的过程
- 每个长方形中有24个小方块，表示24种人名输入后的神经元激活情况
- 对于小方块来说，白色代表正值，黑色代表负值，大小代表绝对值大小
- 24个方块分为两行，第一行是英国人，第二行是意大利人
可视化结果分析：
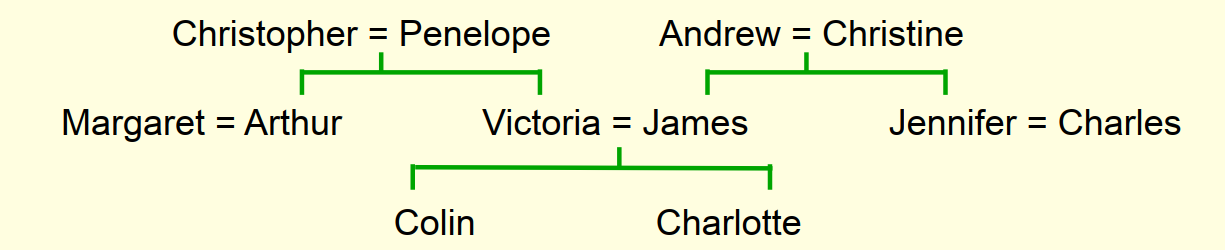
- 6个神经元其实相当于神经网络自动构建了6个特征
- 右上角的神经元很明显构建了区分国籍的特征，毕竟英国人的孩子一般还是英国人，而不会是意大利人，这个特征让模型可以排除掉一半的错误答案
- 左下角的神经元所有的黑色小方块都对应了家谱树的右半部分人名
- 右下角的神经元最大的八个黑色小方块对应了辈分最高的那一代人名
- 右中间的神经元最大的四个黑色小方块对应了辈分最低的那一代人名
模型的有效性
- 隐藏层神经元充分学习到了对预测有益的自构建特征
- 保留了4个样本作为测试集，实现了75%的准确度
- 很少的样本就能让神经网络学习到极为优秀的特征表示
模型应用
- 对于任何满足（A R B）格式的三元组，都可以借助神经网络，实现通过其中任意两个预测第三个的建模，也可以实现这三项输入的低维特征表示
- 建模成功后，也可以反过来对数据进行纠错，纠正一些诸如爷爷的爸爸是儿子的问题
- 在拥有充足可靠的负样本的情况下，也可以输出三元组规则的可靠性评估（规则正确或错误的概率）
2 认知科学简述
A brief diversion into cognitive science
2.1 概念到底该如何表示呢？
特征论：概念由一系列语义特征的表示
- 便于解释概念之间的相似性
- 便于将概念表示为向量
结构主义论：概念不是孤立的，由与其它概念的关系决定
- 概念应该是关系图谱中的一个节点
- Minsky将感知机的不足作为论据反驳特征论，支持结构主义论
两种论点不应该是对立的：
- 关系图谱也可以由语义特征向量来表示，这一点在上一节中的家谱关系建模中就体现的淋漓尽致了，老爷子真的是用心良苦呀！
- 神经网络并没有构造显式的关系图谱或在关系图谱上做显式的推断，而只是将特征在不同层之间进行传播。
- 通过有意识的推理或深思熟虑，可以得到很多明确的规则，但是很多常识和类比推理都是像神经网络模型一样直接给出答案的。
- 即使是明确了很多规则，这些规则如何应用有时候也不是显式的。
- 神经网络的基本逻辑单元是二元的（yes or no），而现实中存在着很多离散的标签（权重只能描述强弱，而不能表示真正关系）或者高维逻辑（A is between B and C），这都是神经网络需要付出很多代价去克服的。
- 如何正确的通过神经网络构建关系知识依然是一个悬而未决的事情，目前的神经网络只能做到概念的“distributed representation”，即一个概念被多个神经元表示，每个神经元同时参与到多个概念的表示。
3 softmax输出函数
Another diversion: The softmax output function
3.1 均方误差的不足
数过小时，权重无法快速更新：
- 根据求导公式$\frac{\partial{E}}{\partial{w_i}}= \sum_nx_i^ny^n(1-y^n)(t^n-y^n)$可知
- 当$t=1$而$y$趋近于0时，$\frac{\partial{E}}{\partial{w_i}}$趋近于0，最终导致权重几乎不会更新
输出的概率没有归一化：
- 所有结果的概率加和应该等于1
- 改进方案是使用softmax强制输出表示一个概率分布
- 当然损失函数也免不了需要相应的修改
而这就引出了本小节的Softmax函数
3.2 Softmax函数
softmax单元的输出并不仅仅取决于输入$z_i$，而取决于整个分组的输入
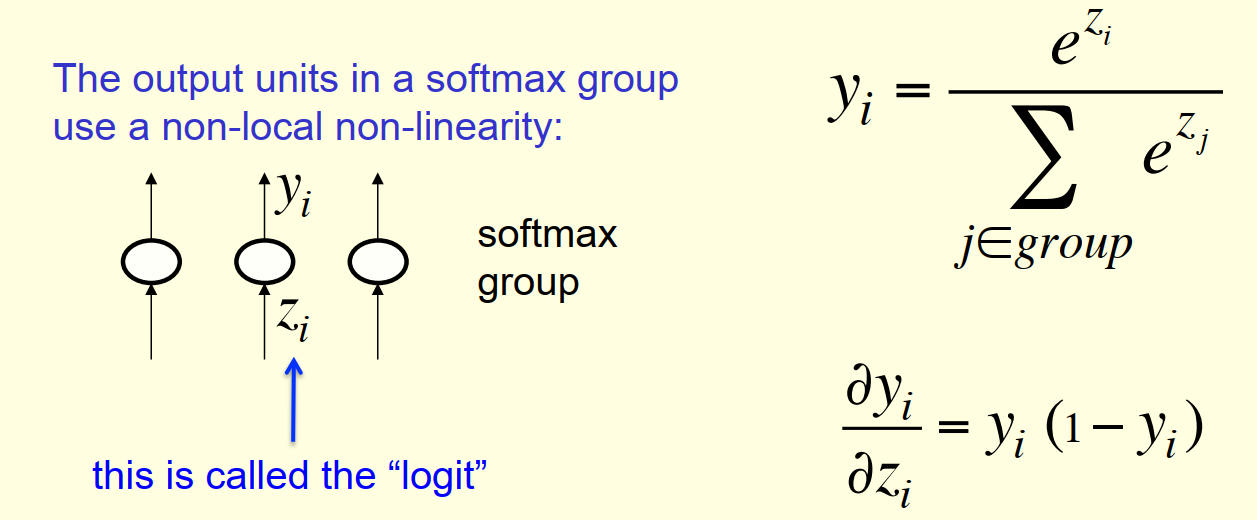
3.3 Cross-entropy 交叉熵
Cross-entropy 交叉熵损失函数： $$C=-\sum_jt_jlogy_j$$ 其中$t$表示真实值，$y$表示预测值
函数求导： $$ \begin{align} \frac{\partial{C}}{\partial{z_i}}& = \sum_j\frac{\partial{C}}{\partial{y_j}}\frac{\partial{y_j}}{\partial{z_i}} \ \\ & = \sum_{j=i}\frac{\partial{C}}{\partial{y_j}}\frac{\partial{y_j}}{\partial{z_i}} +\sum_{j\neq i}\frac{\partial{C}}{\partial{y_j}}\frac{\partial{y_j}}{\partial{z_i}} \ \\ & = (-\frac{t_i}{y_i})y_i(1-y_i) +\sum_{j\neq i}(-\frac{t_j}{y_j})(-y_iy_j) \ \\ & = (-t_i)(1-y_i) +\sum_{j\neq i}(t_jy_i) \ \\ & = y_i\sum_{j}t_j-t_i \ \\ & = y_i-t_i \end{align} $$ 其中$y_i\sum_{j}t_j=y_i$是因为$t_j$表示真实值，是一个one-hot向量 而$\frac{\partial{y_j}}{\partial{z_i}}=(-y_iy_j)$则推导如下： $$\begin{align} \frac{\partial{y_j}}{\partial{z_i}}& = \frac{\partial{(\frac{e^{z_j}}{\sum_{k\in group}e^{z_k}})}}{\partial{z_i}} \ \\ & = e^{z_j}\frac{-1}{(\sum_{k\in group}e^{z_k})^2}e^{z_i} \ \\ & = (-y_iy_j) \end{align}$$
优势分析
- 当$t=1$而$y$趋近于0时，$y_i-t_i$能保证权重的更新
- $\frac{\partial{C}}{\partial{z_i}} = y_i-t_i$和$\frac{dy}{dz} = y_i(1-y_i)$互相起到了某种平衡作用
4 神经概率语言模型
Neuro-probabilistic language models
4.1 trigram模型
通过大量数据的统计结果来得到条件概率
$p(w_3=c|w_2=b,w_1=a)$表示前两个词分别为a和b的情况下，第三个词为c的概率
这种方式在深度学习盛行之前，一度是语言学习的最优解
缺点分析
- 扩大上下文（如考虑前五个词），会导致统计量飙升，同时会出现大量出现次数为0的组合
- 虽然实际统计次数为0，但是理论出现概率可不一定是0啊
- “母鸡下蛋”和“母鸭下蛋”对于trigram模型是毫无关联的独立事件，这使得模型利用的信息非常的浅显，模型不知道“母鸡”和“母鸭”存在相似之处，也更不会得出诸如“母鸡和母鸭都是卵生/雌性/哺乳动物”的一些深层特征。
4.2 神经网络语言模型
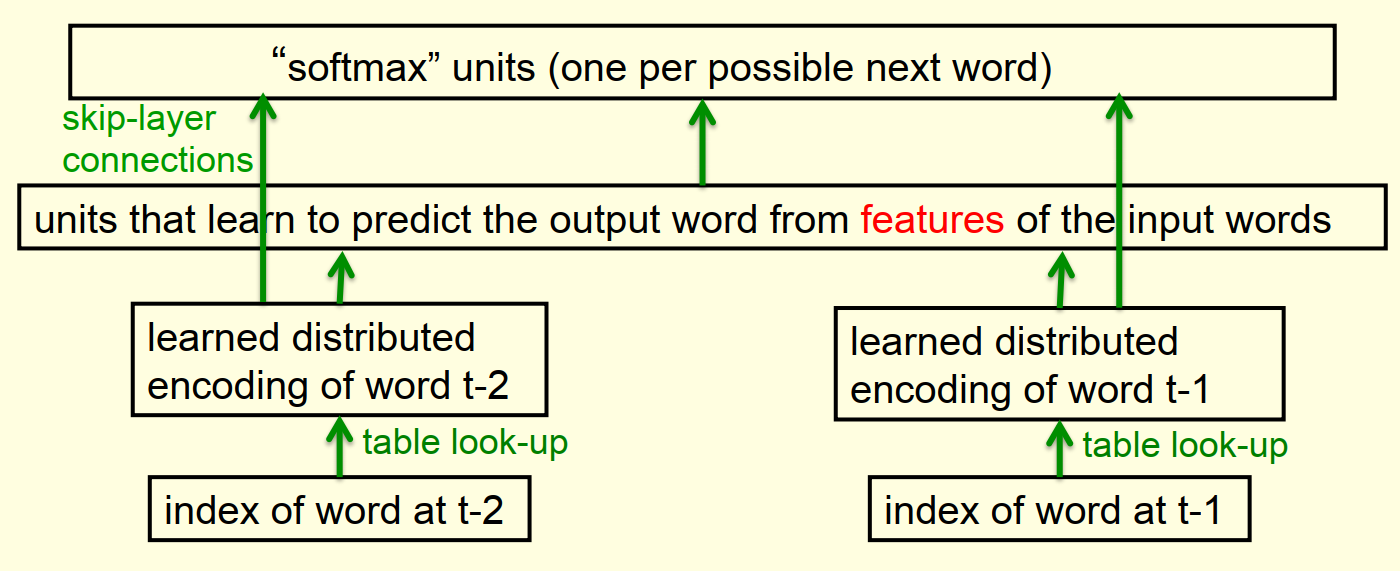和上文的6_course/深度学习/Hinton机器学习与神经网络/4.《机器学习与神经网络》词的向量表达#1.2 神经网络结构如出一辙
输出的维度灾难
- 如果数据集的词表总共包含10w个词
- 这就要求隐藏层神经元的输出也应该是10w维的
- 建模成本过高，而且需要海量的训练集支持
- 缩小隐藏层的输出维度，又会降低最终预测的精度
5 处理大量输出的方法
Ways to deal with the large number of possible outputs in neuro-probabilistic language models
5.1 序列架构
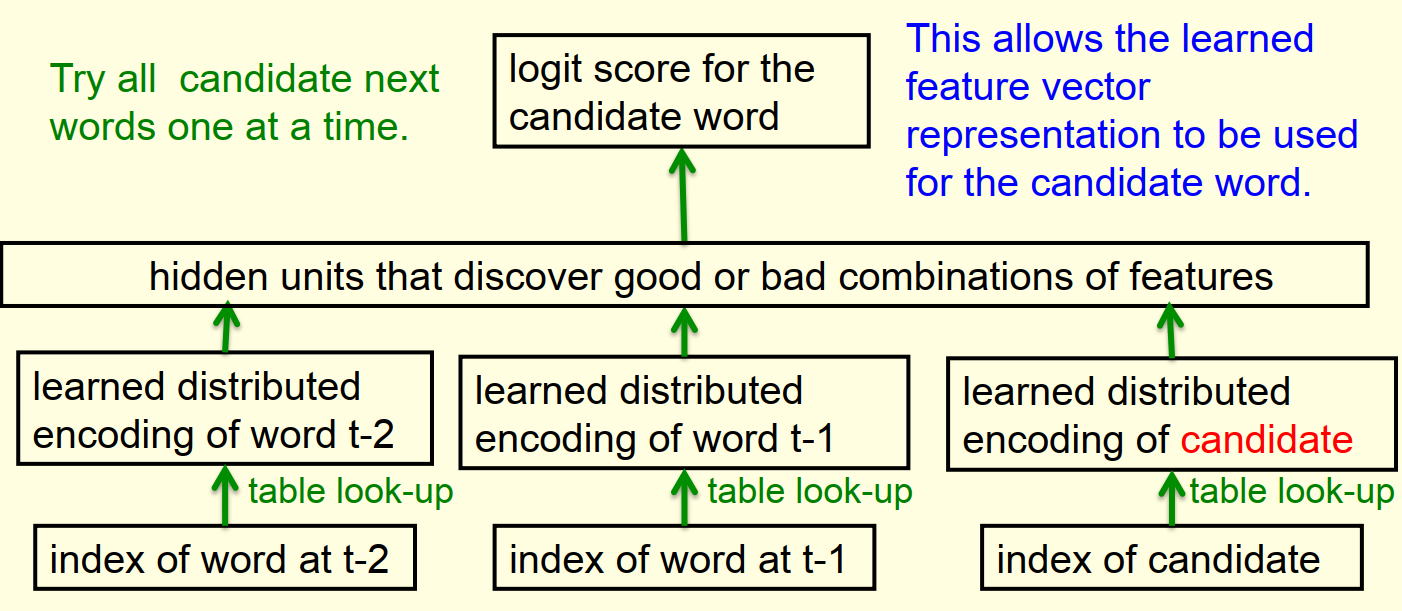
探针法，输出层不再一下子输出10w个词语对应的概率，而只输出待检测的词语对应的概率。
训练过程
- 计算所有候选词的logit score，代入softmax得到概率
- 计算cross-entropy，利用导数更新weights
- 如果有其他predictor提供的小集合的候选词的话，可以省下很多时间
5.2 二叉树架构
另一种避免10w词灾难的方法是利用二叉树将词语二进制编码
词语二进制编码
- 词语被表示为平衡二叉树的叶子
- 每一个词语可以被从根节点到叶节点的唯一路径表示
- 这个路径本身可以被表示为一个二进制串
- 二进制串中1表示搜索当前节点的左子结点，0则是右节点
- 最终，每个词可以被表示成一串二进制码
此方法由Minih 和 Hinton在2009提出，具体可参考word2vec中的Hierarchical Softmax
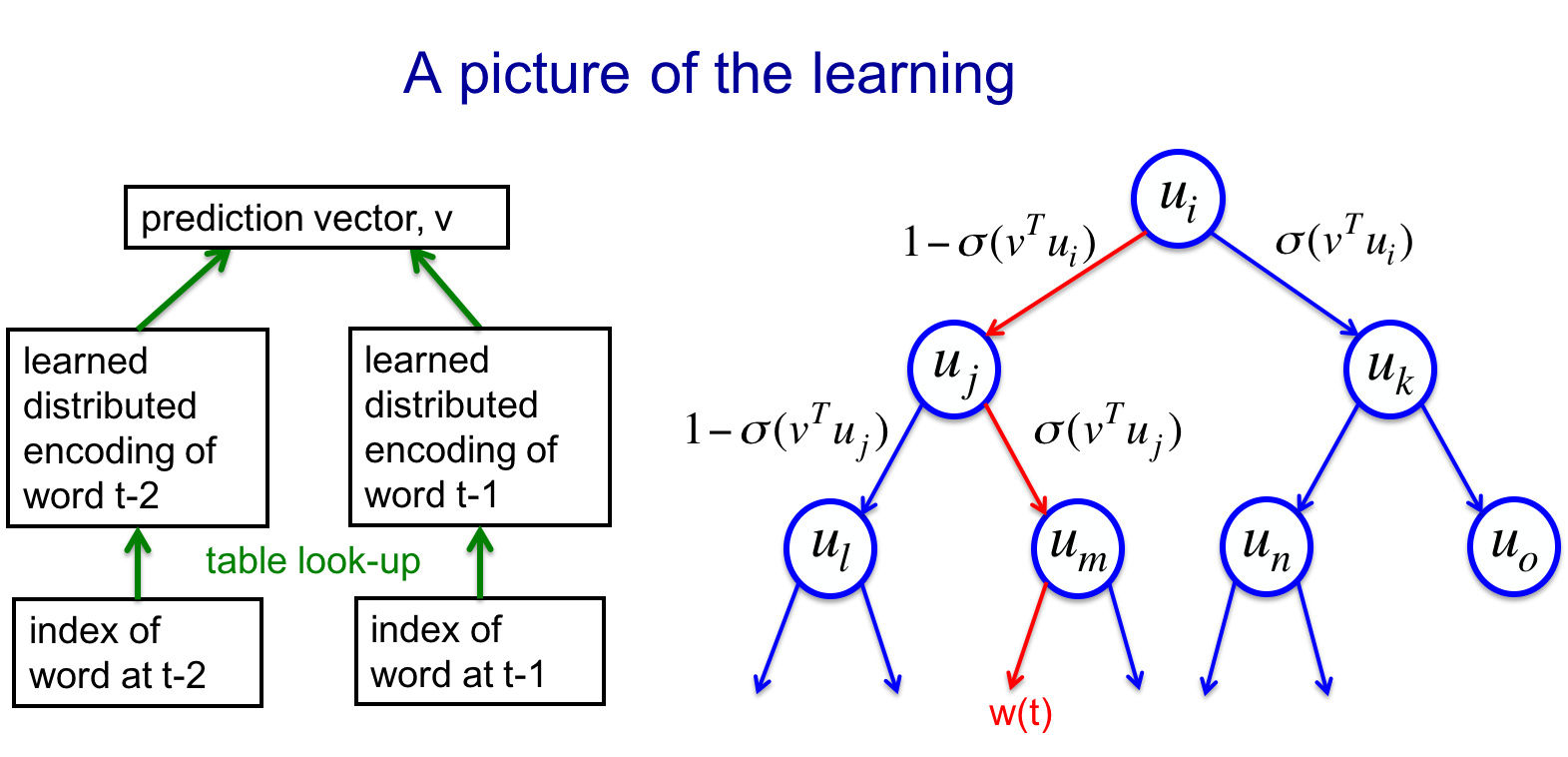
训练过程
- 使用神经网络得到预测向量v，然后进入二叉树并进行路径选择
- 优化目标为最大化目标单词的log概率，相当于最大化路径上所有经过节点的log概率之和，所以损失函数可定义为W(t)=路径节点的概率的负对数
- 损失函数也将反过来更新权重和每个非叶子节点对应的向量u
最终效果
- 层次化NPLM（神经网络语言模型），比普通的NPLM快2个数量级，因为模型只需进行log（N）次决策，而不再计算全集的N个词语。也就是用log（N）个sigmoid函数取代了N维的softmax函数
- 不幸的是，这么做依然很慢。（毕竟树的构建成本+log（N）个sigmoid函数计算，依然还摆在那呢）
5.3 随机负样本
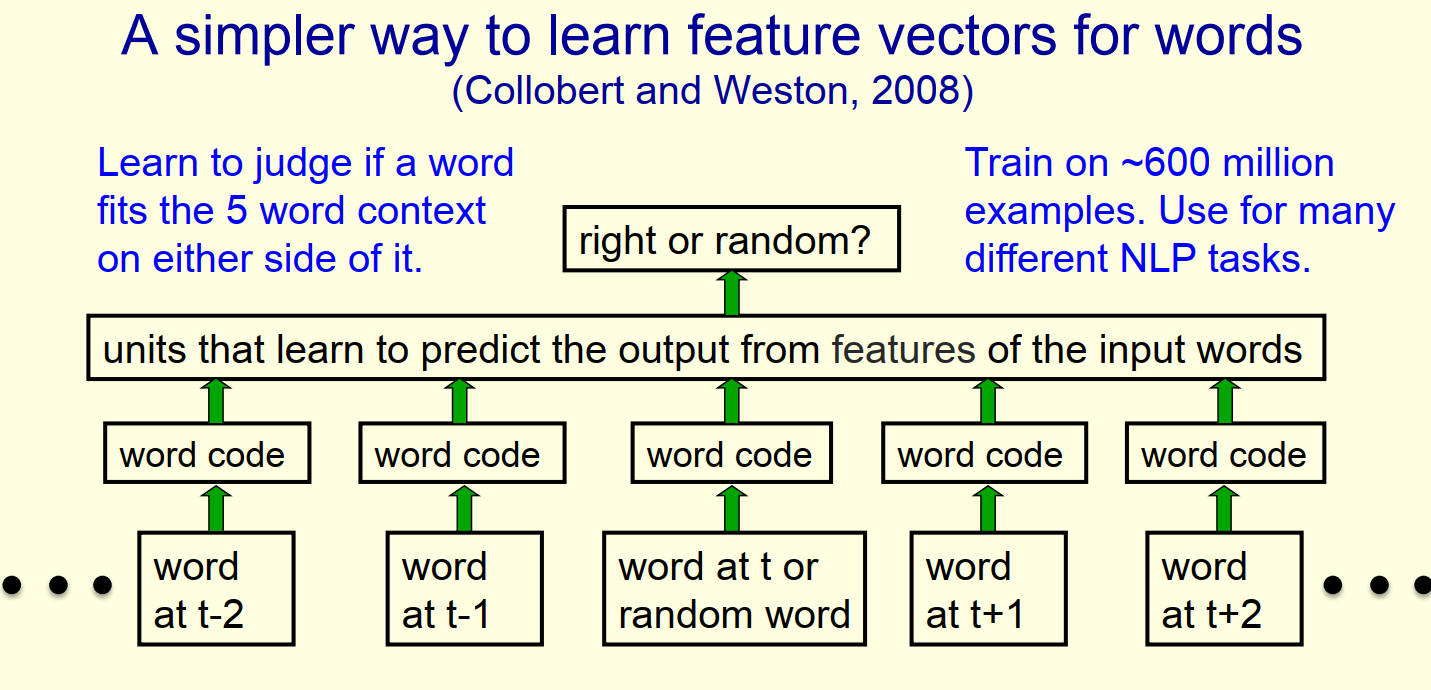
滑动窗口的方式，随机替换中间的词语，形成负样本 之后在海量文本中训练，得到了优秀的词语编码向量
可视化评价
- 采用t-sne进行降维可视化
- 语义相近的词语在空间上也更接近
- 无需样本标注，相当于无监督学习了
参考
word2vec中的Hierarchical Softmax Hinton神经网络公开课4 Learning feature vectors for words