1 信息
信息是不确定性的减少或消除——香农
对于随机变量$X$来说,其取值可能为${x_0,x_1,...,x_n}$
假设变量$X$对应的概率分布为$p$,则$X=x_0$的信息量为 $$I(x_0)=-log(p(x_0))$$
2 熵
熵(entropy)度量了事物的不确定性
不确定越高的事物,它的熵就越大。
随机变量X的熵可以表示如下:
$$H(X)=-\Sigma_{i=1}^np_ilog(p_i)$$
- 其中$n$表示$X$的所有取值的可能数量
- $p_i$表示$X$取值为$i$的概率
- $log$函数一般以2或者e为底
- 熵是不同取值对应信息量的加权累积
2.1 联合熵
两个变量X和Y的联合熵表达式: $$H(X,Y)=-\Sigma_{x_i\in X}\Sigma_{y_i\in Y} p(x_i,y_i)log(p(x_i,y_i))$$
2.2 条件熵
用于度量在已知条件Y的情况下,变量X依然保留的不确定性。表达式如下: $$H(X|Y)=-\Sigma_{x_i\in X}\Sigma_{y_i\in Y} p(x_i|y_i)log(p(x_i|y_i))$$
3 信息增益
H(X)度量了X的不确定性,条件熵H(X|Y)度量了我们在知道Y以后X剩下的不确定性
H(X)-H(X|Y)度量了X在知道Y以后不确定性减少程度,在信息论中称为互信息, 记为I(X,Y)。
互信息I(X,Y)在决策树ID3算法中也叫做信息增益(mutual information,information gain)
熵与信息增益的关系如下:
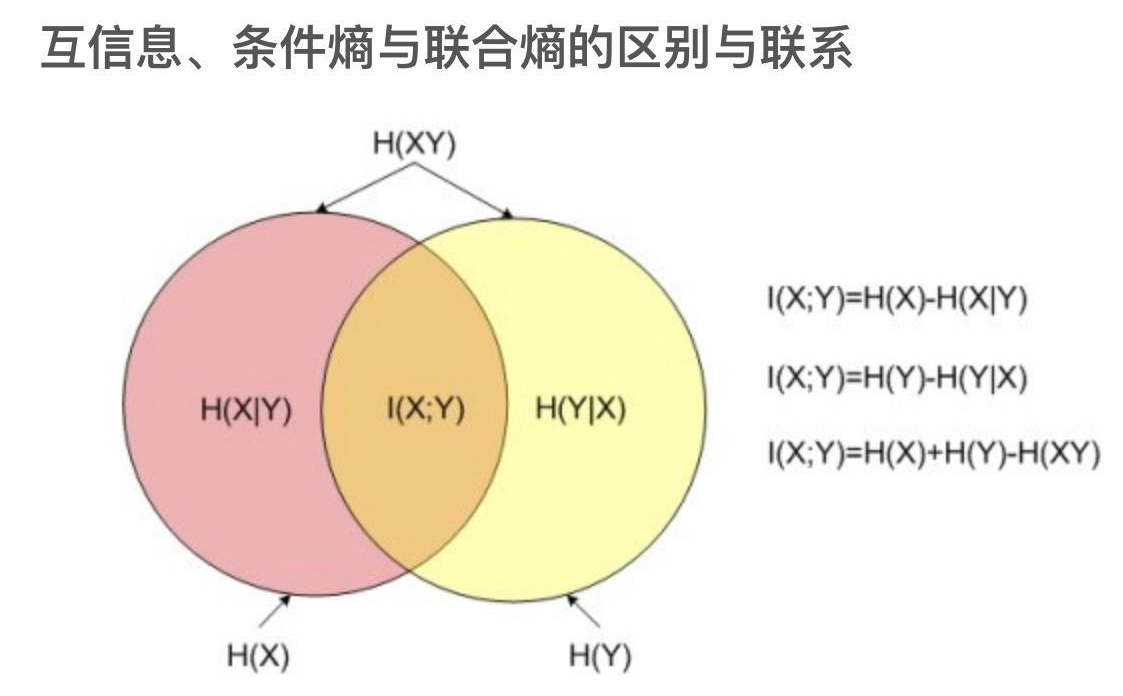
$I(X,Y)=H(X)-H(X|Y)=H(Y)-H(y|X)$,这描述了互信息的一种对称性
3.1 信息增益比
信息增益与熵的比值:$I(X;Y)/H(X)$
4 基尼系数
在分类问题中,假设有$K$个类别,第$k$个类别的概率为$p_k$, 则基尼系数的表达式为: $$Gini(p)=\Sigma_{k=1}^Kp_k(1-p_k)=1-\Sigma_{k=1}^Kp_k^2$$
基尼系数代表了模型的不纯度,基尼系数越小,则不纯度越低,特征越好。这和信息增益(比)是相反的。
5 KL散度
KL散度(Kullback–Leibler Divergence, 相对熵):随机变量x取值的两个概率分布p和q,用来衡量这2个分布的差异,通常用p表示真实分布,用q表示预测分布。则q对p的KL散度定义如下: $$KL(P||Q)=\Sigma_{i=1}^n p_i\times log(p_i/q_i)=\Sigma_{i=1}^n p_ilog(p_i)-\Sigma_{i=1}^np_ilog(q_i)$$ n为事件的所有可能性,如果两个分布完全相同,那么它们的相对熵为0。如果相对熵KL越大,说明它们之间的差异越大,反之相对熵KL越小,说明它们之间的差异越小。
6 交叉熵
交叉熵(Cross Entropy)是交叉熵和KL散度的公式非常相近,其实就是KL散度的后半部分: $$H(P,Q)=-\Sigma_{i=1}^np_ilog(q_i)$$ $$KL(P||Q)=\Sigma_{i=1}^n p_ilog(p_i)-p_ilog(q_i)=H(P,Q)-H(P)$$ 在分类问题中,随机变量的真实分布p(x)是确定的,于是H(p)也是确定的,相当于一个常数。此时,优化KL散度与优化交叉熵等价,因此二者都常作为分类问题的损失函数
这里的交叉熵$H(P,Q)$注意和上文的联合熵$H(X,Y)$区分,二者符号容易混淆;但$X,Y$是两个不同的变量,$P,Q$是两个需要对比的分布,二者的含义是完全不同的