t-SNE 算法
- 全称为 t 分布-随机邻近嵌入(t-distributed Stochastic Neighbor Embedding)
- 该算法将高维空间中的数据映射到低维空间中,并保留数据集的局部特性
- t-SNE 算法能够捕捉数据间的非线性关系,数据可视化效果好,常用于探索性数据分析
- t-SNE 算法的缺点主要是占用内存较多、运行时间长,容易丢失大规模信息 (集群间关系)
算法过程概述:
- 计算原始高维空间中数据点之间的相似度:对于样本 $i$,算法会使用以 $i$ 为中心的高斯分布来计算其他数据点的条件概率 $P_{j|i}$,进而得到样本 $i$ 和样本 $j$ 在高维原始空间的相似度 $P_{i,j}$
$$ P_{j|i}=\frac{\exp(-||x_{i}-x_{j}||^2/2\sigma^2)}{\Sigma_{j}\exp(-||x_{i}-x_{j}||^2/2\sigma^2)} , \ \ \ \ \ P_{ij}=\frac{P_{j|i}+P_{i|j}}{2N} $$
$\sigma$ 是可调节的超参数(perplexity);$N$ 表示样本数;右侧公式是为了确保相似度矩阵的对称性
- 计算低维嵌入空间中数据点之间的相似度,先使用 $t$ 分布(一般自由度为 1)随机初始化所有样本的位置,样本间的相似度 $Q_{ij}$ 的计算同高维空间中的计算过程(只是不再需要额外的对称化处理)
- 定义目标函数为原始空间和嵌入空间的联合概率分布的KL散度,然后通过梯度下降法更新样本在嵌入空间的位置,追求低维空间中的样本间相似度尽可能接近高维空间中的相似度
长尾性质:t 分布的长尾性质允许在低维空间中更好地分离远离的点,这有助于避免 PCA 降维中容易存在的“拥挤”现象,即在低维空间中不同簇之间的点被压缩在一起
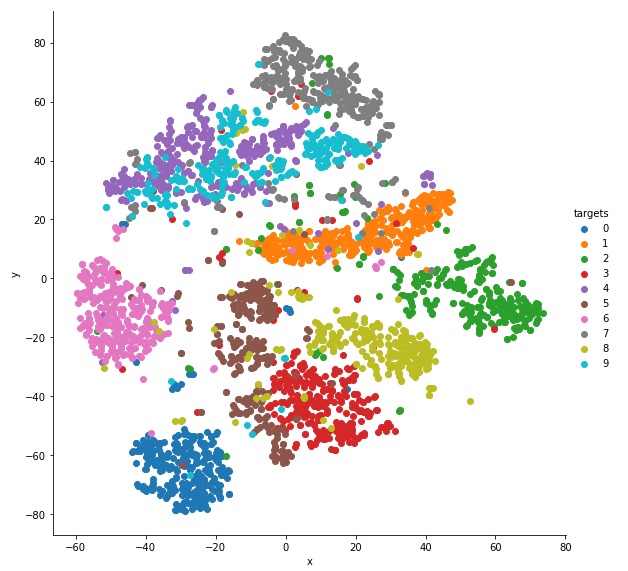
t-SNE 算法示例:
# 基于 t-SNE 算法对手写数字数据集 MINIST 进行可视化
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from sklearn import datasets
from sklearn import manifold
%matplotlib inline
# 获取 MNIST 数据集(国内网络可能下载失败)
data = datasets.fetch_openml(
'mnist_784', version=1, return_X_y=True)
pixel_values, targets = data
targets = targets.astype(int)
single_image = pixel_values[1, :].reshape(28, 28)
# plt.imshow(single_image, cmap='gray') 单个样本的可视化
# 对数据进行t-SNE转换
tsne = manifold.TSNE(n_components=2, random_state=42)
transformed_data = tsne.fit_transform(pixel_values[:3000, :])
tsne_df = pd.DataFrame(
np.column_stack((transformed_data, targets[:3000])),
columns=["x", "y", "targets"])
tsne_df.loc[:, "targets"] = tsne_df.targets.astype(int)
grid = sns.FacetGrid(tsne_df, hue="targets", size=8)
grid.map(plt.scatter, "x", "y").add_legend() # 可视化