流形学习降维 UMAP
发表评论
13 views

UMAP 算法

  • 全称为均匀流形近似与投影，Uniform Manifold Approximation and Projection
  • UMAP 是一种基于黎曼几何和代数拓扑理论框架的数据降维与可视化算法
  • UMAP 能同时捕捉数据的局部和全局结构，可拓展性强，对嵌入维度没有限制
  • MAP 不具备PCA 或因子分析等线性技术可以提供的解释性（因子载荷）

UMAP 定义的概念解释与补充：

  1. Uniform 均匀假设：通过空间的扭曲，对样本稀疏/密集的位置进行收缩或拉伸
  2. Manifold 流形：一种拓扑空间，每个点的附近局部类似于欧几里得空间
  3. Approximation 近似：用一组有限的样本组（而不是完整集合）来近似流形
  4. Projection 投影：空间对象从高维空间到低维空间的映射

由于均匀假设（空间是扭曲的），导致距离的度量只能是局部的，而不是整个空间通用的

常见的一维流形：线和圆，但不包括类似数字8的形状 常见的二维流形（又名曲面）：平面、球体、环面等

UMAP 的算法过程分两步：（1）学习高维空间中的流形结构（2）找到该流形的低维表示

步骤 1：学习高维空间中的流形结构（图源 - UMAP 官方文档）：

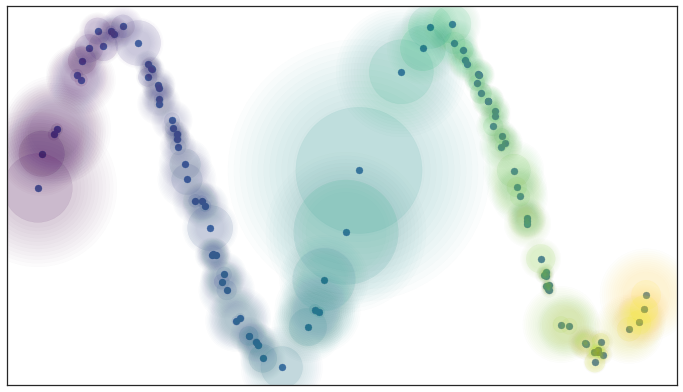
  1. 使用 k 近邻算法找到每个样本点在高维空间中的 $k$ 个近邻点，组成 $k$ 邻域图
  2. 计算样本点 $i$ 及其近邻点 $j$ 之间的距离 $d_{ij}$，用于 $k$ 邻域图边权重 $w_{ij}$ 的初始化 $$

w_{ij}=\exp(\frac{-max(0,d_{ij}-\rho_{i})}{\sigma_{i}}) $$ - $k$ 最近邻的数量，用于控制算法抽取数据的局部或全局结构；$k$ 取值越小，算法的降维结果更倾向于捕捉原始数据中的局部结构；$k$ 取值越大，算法的降维结果更倾向于捕捉原始数据中的全部结构 - $\rho_{i}=min(d_{ij}|1\leq j \leq k,d_{ij}>0)$ ，该参数的选择描述了 $k$ 邻域图的局部连通性约束（一般默认值=1），即每个节点至少与其他一个节点相连的概率为 100% - $\sigma_{i}$ 对应平滑归一化因子，取值的经验公式如下：$\sum_{j\mathop{=}1}^{k}\exp\left({\frac{-\operatorname*{max}(0,d(x_{i},x_{i_{j}})-\rho_{i})}{\sigma_{i}}}\right)=\log_{2}(k).$ 3. $k$ 邻域图的加权邻接矩阵 $A$ 的对称化处理：$B=A+A^{\mathsf{T}}-A\circ A^{\mathsf{T}}$

对称化处理深入理解：假设节点 a 和节点 b 之间存在两个权重边 $w_{ab}$ 和 $w_{ba}$，对称化处理也对应着边的合并操作 $w_{ab}+w_{ba}-w_{ab}\cdot w_{ba}$；如果原始边权重对应边的存在概率，那合并后的边权重就是至少存在一条边的概率

最终得到了满足局部连通性约束的邻域图（高维空间中的流形结构）：

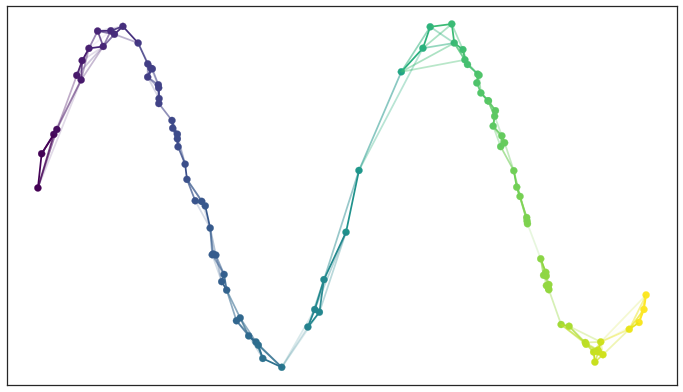
步骤 2：找到该流形的低维表示

  1. 随机初始化样本在低维嵌入空间的位置，并且节点间的距离是非变化的（低维空间不是扭曲的），而是标准的欧几里得距离；但为了避免低维嵌入空间可能存在的节点堆叠的问题，需要限制节点间的最小间距
  2. 以目标函数（交叉熵 CE）最小化为目标，用梯度下降法来指导样本在低维嵌入空间的坐标更新： $$CE=\sum_{e\in E}{w_{h}(e)}{log(\frac{w_{h}(e)}{w_{l}(e)})}+(1-{w_{h}(e)});l o g(\frac{1-{w}_{h}(e)}{1-{w}_{l}(e)})$$
    • $w_{h}(e)$ 表示边 $e$ 在高维空间的边权重；$w_{l}(e)$ 表示边 $e$ 在低维空间的边权重
    • 交叉熵的前项描述了样本在高维空间中的“吸引力”，$w_{h}(e)$ 越大，前项越小
    • 交叉熵的后项描述了样本在高维空间中的“互斥力”，$w_{h}(e)$ 越小，后项越小

Python 实现 - 官方 github 地址

UMAP 的四个常用超参数：

  1. n_neighbors：指定最近邻的数量，用于控制算法抽取数据的局部或全局结构
  2. local_connectivity：默认值为 1 ，意味着每个样本都至少与其他一个点相连
  3. min-dist：默认值为 0.1，低维嵌入空间中节点之间的最小距离（分离度）
  4. n-epochs：用于优化低维嵌入空间中节点表示的训练轮数

local_connectivity 和 n_neighbors 分别决定了领域图节点数的下限与上限

UMAP VS t-SNE

  • 二者都擅长对数据的降维与可视化，都能捕捉到数据中的非线性关系
  • 相比于 t-SNE，UMAP 的算法运行性能更好（速度更快，能保留更多全局结构）
  • 二者在小数据集上表现无明显差距，但在大数据集上更推荐使用 UMAP 算法

不同降维可视化算法的对比（图源 - UMAP 官方论文）：

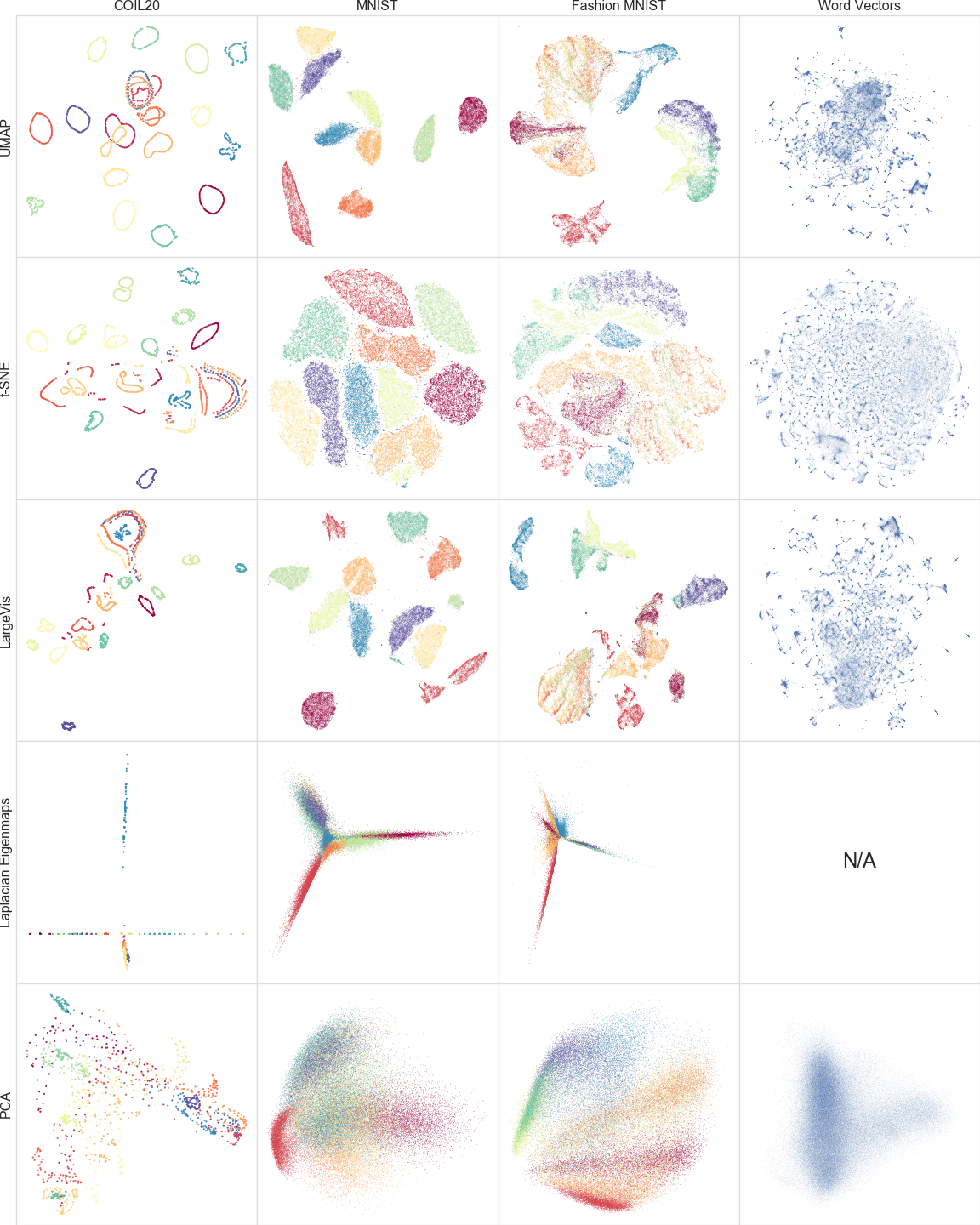
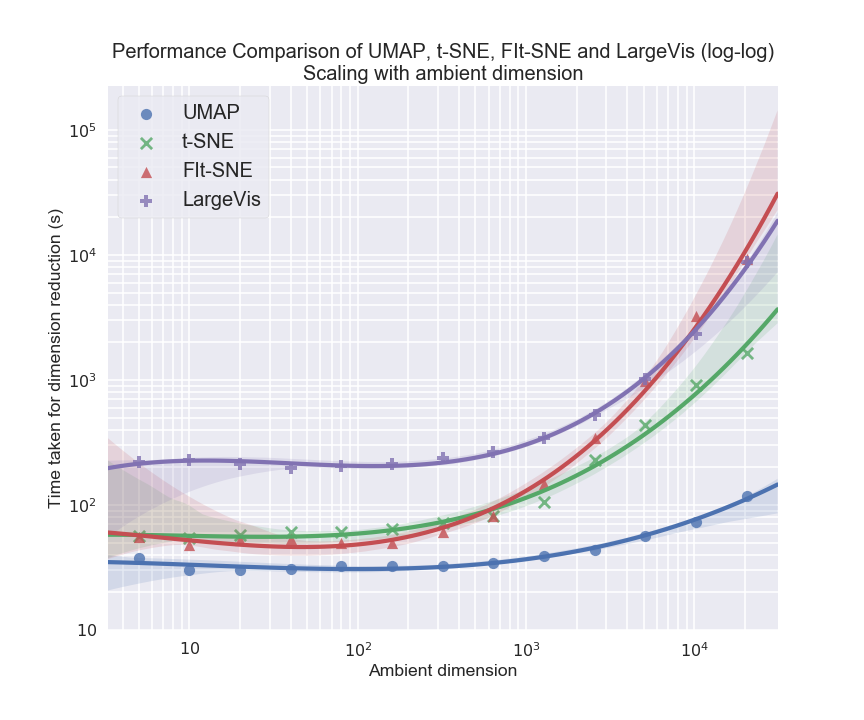
随着数据维度的增加，UMAP 的性能表现明显优于其他模型（图源 - UMAP 官方论文）： 参考：UMAP Dimensionality Reduction — An Incredibly Robust Machine Learning Algorithm

往年同期文章