1 算法概况
Chinese Whispers(简称CW)算法,是一种无监督的图聚类算法
CW算法运行效率高,但结果存在不确定性,常用于人脸聚类或文本聚类
2 算法步骤
以人脸聚类为例,先进行图的初始化(构建无向加权图):每个人脸图片为一个节点,不同节点通过计算相似度,然后连接相似度超出指定阈值的节点,并以相似度作为边的权重
算法步骤
- 对于N个人脸样本,每个样本节点先单独成簇(自成一类)
- 遍历所有节点,根据每个节点的邻节点所属类别,计算权重累加
- 修正节点类别,选择最终累加权重最高的类别
- 如果有多个权重最高的类别,则随机选择其中的一个类别
- 重复步骤2-4,直到不同类间的区域边界趋于稳定(或者达到最大迭代次数)
算法的收敛过程示意:
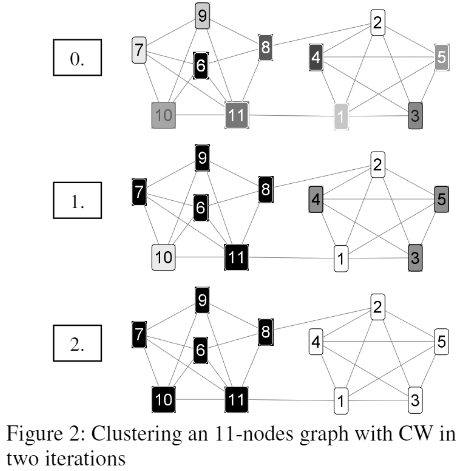
其中类别的不同用颜色的深浅来表示;可以发现对于节点数为11的图来说,仅仅两次迭代就完成了收敛,并且最终聚为2类(当然这个图中的例子是比较理想的情况~)。
算法的迭代次数一般不高,主要取决于图的直径,两个节点之间的距离越大,信息渗透所需要的迭代次数就越多;从另一个角度来说,距离不远的节点,会因为邻接点的“圈地宣示主权”被快速“吞并“或”驱逐“,尤其是”早期发育起来“的类传播很快,收敛速度也因此很快
3 算法分析
主要优点:
- 没有超参(阈值是图初始化时的超参,严格来说不属于算法的超参)
- 效率高,并且可以通过矩阵运算加速(由于最终选择的是最高累加权重的所属类别,所以可以对矩阵进行剪枝,只保留每个列中值较大的情况)
- 适用于有权图和无权图(对于后者可能可能存在收敛慢和不确定性的问题)
主要缺点:
- 由于一开始都单独成类,所以节点数较大时,早期收敛较慢,尤其是对于无权图来说
- 可能存在收敛震荡的情况(一个墙头草节点,不断地两边倒,主要由于算法步骤4的随机选择)
- 孤立节点会被算法忽视,无法参与到聚类过程
- 结果存在一定的不确定性,尤其是对于无权图来说
改进方案:
- 增加随机突变,能有效缓解早期收敛较慢和收敛震荡的问题
- 类保持,一定概率上,不考虑节点类别的修改,提高计算效率,缓解收敛震荡
4 实验结论
- 两个类之间有关联的边越多,耦合性越高,CW算法约难区分这两个类
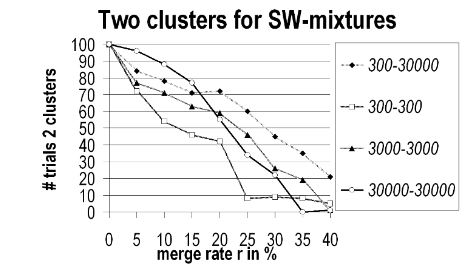
横坐标表示merge rate,指两个类的节点合并率(合并率越高,添加的噪声越多)
纵坐标表示CW算法区分两个类的成功概率
- 无权图可以通过初始化权重都为1的方式,使用CW算法,但是收敛速度会慢很多
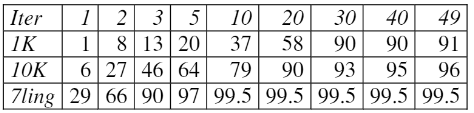
其中数据集1K和10K为无权图,而7ling为有权图,后者仅需要6次迭代便基本收敛