1 高斯过程
给定均值向量和协方差矩阵，可以唯一确定一个高斯分布（Gaussian distribution）
给定均值函数和协方差函数，可以唯一确定一个高斯过程（Gaussian Process，GP）
假设自变量为时间$t$，则每一个时刻$t$，高斯过程都对应着一个高斯分布
当时间$t$是连续型变量时，整个高斯过程便对应着无数个高斯分布，所以高斯过程可看作无限维高斯分布
高斯分布的两个重要性质：
- 数据服从高斯分布时，数据的抽样结果也服从同一个高斯分布
- 数据服从高斯分布时，数据的条件分布也服从高斯分布，并且均值和协方差可以被唯一确定
2 高斯过程回归
高斯过程回归（Gaussian Processes Regression，简称 GPR）是高斯过程在机器学习的简单应用
GPR 假设样本整体服从多维正态分布，并会根据观察序列（训练集）估计联合分布用于新样本的预测
GPR 是一个随机模型，不同于神经网络、决策树等确定性模型，其输出为一个服从高斯分布的随机变量。GPR的实际输出是均值和方差，需要取值时则根据估计分布进行采样，所以GPR的结果是不确定的
2.1 构建先验分布
给定$n$个样本$(X,Y)={(x_i,y_i)}_{i=1}^n$，当输入为$x_i$时，先验分布对应的输出是随机变量$y_i$
所有的随机变量$y$构成一个的多元高斯分布（先验分布）： $$[y_1,y_2,...,y_n]\sim N(\mu,\Sigma) \approx N(0,K)$$
- 其中$\mu$为n维均值向量，由于数据通常会进行标准化处理，所以一般默认为零均值
- $\Sigma$为$n \times n$维协方差矩阵，$K$则是用于近似表示$\Sigma$的协方差函数矩阵，所以$N(0,K)$是高斯过程
- 所以GPR算法的核心在于找到一个高斯过程去尽可能逼近已知的多元高斯分布（先验分布）
$$\Sigma=\left[ \begin{matrix} \sigma_{1,1} & \cdots & \sigma_{1,n} \\ \vdots & \ddots & \vdots \\ \sigma_{n,1} & \cdots & \sigma_{n,n} \\ \end{matrix} \right]\approx K=\left[ \begin{matrix} k(x_1,x_1) & \cdots & k(x_1,x_n) \\ \vdots & \ddots & \vdots \\ k(x_n,x_1) & \cdots & k(x_n,x_n) \\ \end{matrix} \right]$$
- 其中$k$表示核（kernel）函数，常用核函数为高斯核，即径向基函数（Radial Basis Function，RBF）
- 当$x_i$和$x_j$距离较近时，$y_i$和$y_j$也应该是相似的；基于此原理，$y_i$和$y_j$的协方差$\sigma_{ij}$可以替代为核函数$k(x_i,x_j)$
2.2 核函数的选择
假设核函数为径向基函数，则$k(x_1,x_3)$可表示如下： $$k(x_1,x_2)=\sigma^2exp{(-\frac{1}{2l}||x_1-x_2||^2)}$$
- 当$x_1=x_2$时，核函数的结果为1；$x_1$与$x_2$的差异越大，核函数结果趋近于0
- 核函数评估的是$x_1$和$x_2$的相似性，这和协方差$\sigma_{i,j}$的含义是一致的
- 核函数的种类很多，包括但不限于线性核、多项式核、指数核、高斯核
- 其中$\lambda$和$l$是超参数，注意不同书写版本的高斯核函数中超参的形式可能存在差异
- $\lambda$主要控制高斯核的波动程度，$l$主要控制高斯核的影响范围，可视化效果如下：
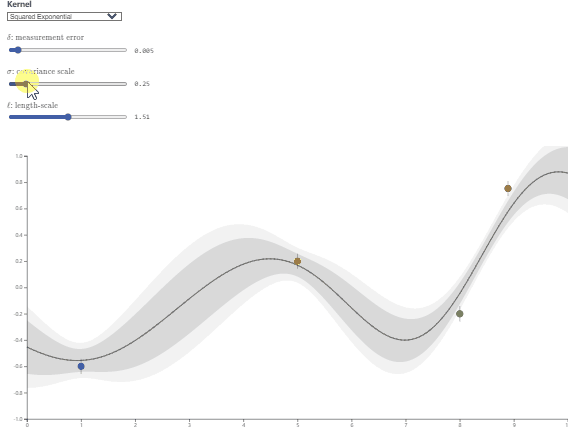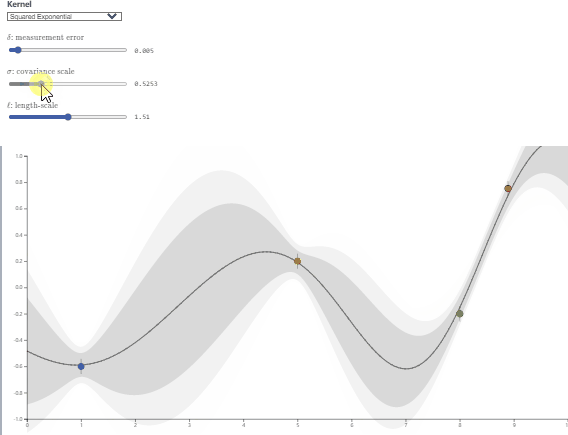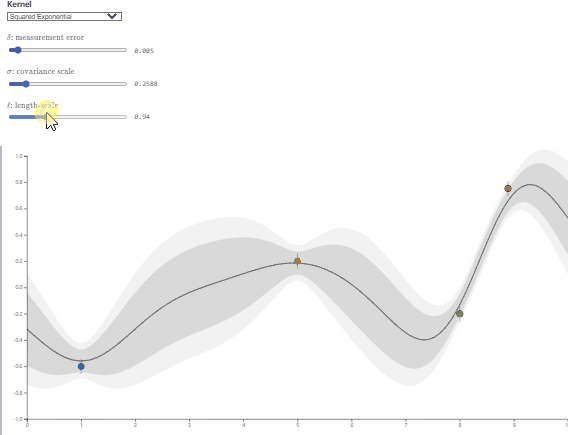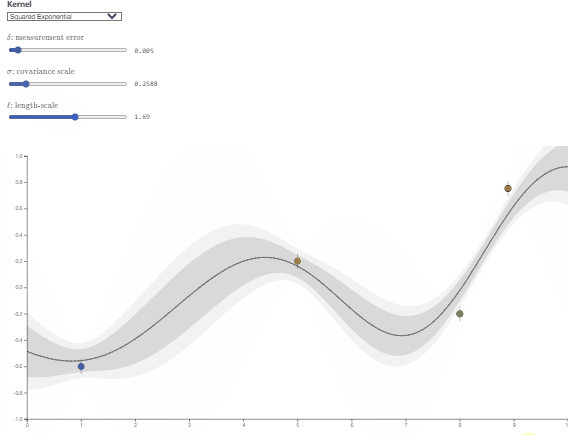图源：https://observablehq.com/@herbps10/gaussian-processes
超参数的估计：
- 最常见的两种方法是极大似然法或MCMC法，细节可参阅 GP超参数的估计
- 极大似然法（maximum likelihood）适合处理凸优化问题，否则容易陷入局部最优
- MCMC法（Markov Chain Monte Carlo）虽然不容易陷入局部最优，但是计算成本高
知识点补充：Mercer 理论
- 核心论点：核函数和协方差矩阵半正定互为充要条件
- 此理论确保了基于核函数所产生的矩阵是一个合法的协方差矩阵
2.3 对新数据进行预测
前置知识：多元高斯分布的条件分布性质
- 假设随机向量$A$和随机向量$B$的联合分布满足以下公式
$$\left[\begin{matrix}A \\ B \\ \end{matrix}\right]\sim N \left( \left[ \begin{matrix} \mu_A \\ \mu_B \\ \end{matrix}\right],\left[ \begin{matrix} \Sigma_A & \Sigma_C \\ \Sigma_C^T & \Sigma_B \\ \end{matrix} \right] \right)$$
- 则在$A$分布已知的情况下，可以推出$B$的条件分布：
$$B|A\sim N(\mu_B+\Sigma_C^T\Sigma_A^{-1}(A-\mu_A),\Sigma_B-\Sigma_C^T\Sigma_A^{-1}\Sigma_C)$$
已知训练集样本为$(X,Y)$，对于新的输入样本$X^{\ast}$，可假设其因变量$Y$和$Y^{\ast}$的联合分布满足： $$\left[ \begin{matrix} Y \\ Y^{\ast} \\ \end{matrix} \right]\sim N\left(0,\left[ \begin{matrix} K(X,X) & K(X,X^{\ast}) \\ K(X^{\ast},X) & K(X^{\ast},X^{\ast}) \\ \end{matrix} \right] \right)\overset{符号简化}{\longrightarrow }N\left(0,\left[ \begin{matrix} K & K_{\ast} \\ K_{\ast}^T & K_{\ast \ast} \\ \end{matrix} \right] \right)$$ 则在$Y$分布已知的情况下，可以推出$Y^{\ast}$的条件分布： $$Y^{\ast}|Y\sim N(K_{\ast}^TK^{-1}Y,K_{\ast \ast}-K_{\ast}^TK^{-1}K_{\ast})$$ 所以在$X$、$Y$、$X^{\ast}$、$K$已知的情况下，根据上式可以轻松得到$Y^{\ast}$的分布情况
3 高斯过程深入理解
3.1 高斯过程可视化
- 由于GPR的结果是随机变量的分布，所以可以进一步给出每个预测结果的置信区间
- 随着$(x_i,y_i)$的给出，与$x_i$相关的核函数$k$会逐渐收敛并确定，反应在输出上便是置信区间的收缩
- 由于相近的输入会得到相近的输出，所以通过核函数逼近协方差矩阵还能起到平滑的作用
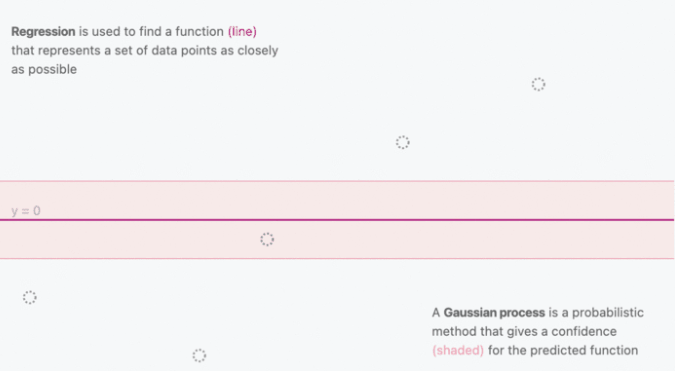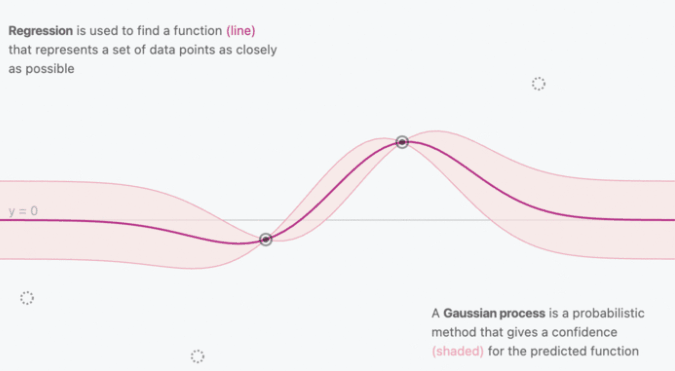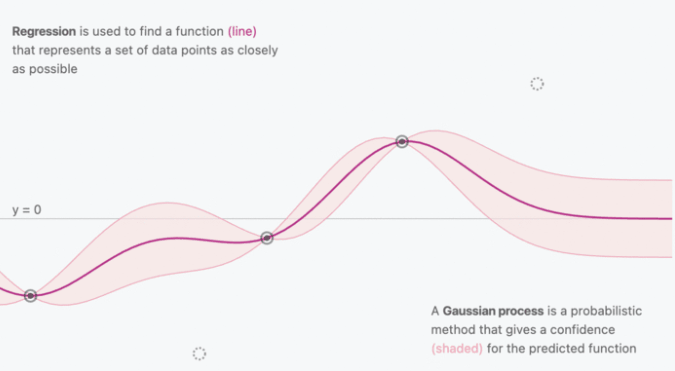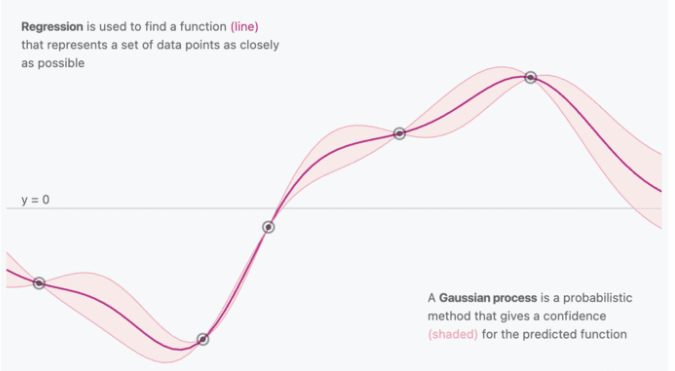
图源：https://distill.pub/2019/visual-exploration-gaussian-processes/
3.2 高斯过程与Ridge回归
假设观测值是有噪音的，则$y=f(x)+\epsilon$，其中$\epsilon \sim N(0,\sigma_y^2)$。
因变量$Y$和$Y^{\ast}$的联合分布进行相应调整： $$\left[ \begin{matrix} Y \\ Y^{\ast} \\ \end{matrix} \right]\sim N\left(0,\left[ \begin{matrix} K+\sigma_y^2I_N & K_{\ast} \\ K_{\ast}^T & K_{\ast \ast} \\ \end{matrix} \right] \right)$$ 条件分布也需要稍微转换一下（$K$换为$K+\sigma_y^2I_N$）： $$Y^{\ast}|Y\sim N(K_{\ast}^T(K+\sigma_y^2I_N)^{-1}Y,K_{\ast \ast}-K_{\ast}^T(K+\sigma_y^2I_N)^{-1}K_{\ast})$$ Ridge回归是通过2-范数进行正则化的线性回归，其对应的回归系数解析解如下： $$\hat{\theta}= (X^TX+\delta^2I_d)^{-1}X^Ty $$ 当针对新样本$X^+$进行预测时，$Y^+$可表示如下： $$Y^+=X^+\hat{\theta}= (X^TX+\delta^2I_d)^{-1}X^+X^Ty $$ 当$X^+ X^T=K_{\ast}^T,\ X^TX+\delta^2I_d=K+\sigma_y^2I_N$时，回归预测的$Y^+$与条件分布$Y^{\ast}|Y$的均值是等价的
结论：Ridge回归是一种考虑噪声的简单高斯过程回归，其对应的核函数的点积运算