中文标题:基于动态辩论的知识图推理
英文标题:Reasoning on Knowledge Graphs with Debate Dynamics
发布平台:AAAI
Proceedings of the AAAI Conference on Artificial Intelligence
发布日期:2020-04-03
引用量(非实时):32
DOI:10.1609/aaai.v34i04.6600
作者:Marcel Hildebrandt, Jorge Andres Quintero Serna, Yunpu Ma, Martin Ringsquandl, Mitchell Joblin, Volker Tresp
文章类型:journalArticle
品读时间:2022-03-23 16:19
1 文章萃取
1.1 核心观点
本文提出了一种基于辩论流程的知识推理框架R2D2。R2D2包含两个持相反论点的Agent用于搜寻论据,以及一个用判决论据合理性的Jundge。R2D2先进行 Jundge的训练使得模型具备初步的论点判断能力,之后将Jundge的判断结果转化奖惩值,通过强化学习的方法进行优化迭代论据的搜集过程。通过这种Jundge和Agent的交替训练,最终的R2D2在知识三元组分类和知识推理任务中均表现出色。
1.2 综合评价
- 对抗式的特征生产,充分发掘论点与反驳点,模型鲁棒性强
- 论据的提出与判断过程符合人类直觉,也极大地改善了模型可解释性
- 符号使用存在冗余,算法部分细节过于简略,阅读体验不高
1.3 主观评分:⭐⭐⭐⭐⭐
2 精读笔记
2.1 背景介绍
知识图谱(KG)借助三元组(主 s、谓 p、宾 o)的形式描述现实世界中大量信息,知识图谱广泛应用于 AI 任务(实体消歧、视觉关系检测、协同过滤等)。常见的大型 KG 包括 0_life/精品资源/数据资源/知识图数据资源#FreeBase、0_life/精品资源/数据资源/知识图数据资源#YAGO、Google KG,但都难以避免信息遗漏或信息错误的问题。
机器学习的可解释方法主要分为后解释与集成透明两种,其中前者是对黑盒模型的结果分析(比如Shap或其他类似的方法),后者则使用集成算法内部解释机制(比如随机森林计算特征重要性)或者单模型本身具备可解释性(比如线性模型)。
本文提出的R2D2(Reveal Relations using Debate Dynamics)模型,希望在不影响性能的情况下,借助KG增强模型的可解释性。具体来说,本文将基于强化学习训练两个论点相反的辩手(辩手其实是一种自动寻找稀疏、可解释的特征的策略),在图谱中寻找最能支持己方观点的论据(论据可理解为事实描述,对应KG中的一条链路),然后借助裁判(分类器)判定最终正确的论点
以论证”迈克尔乔丹是否是专业篮球运动员“为例:
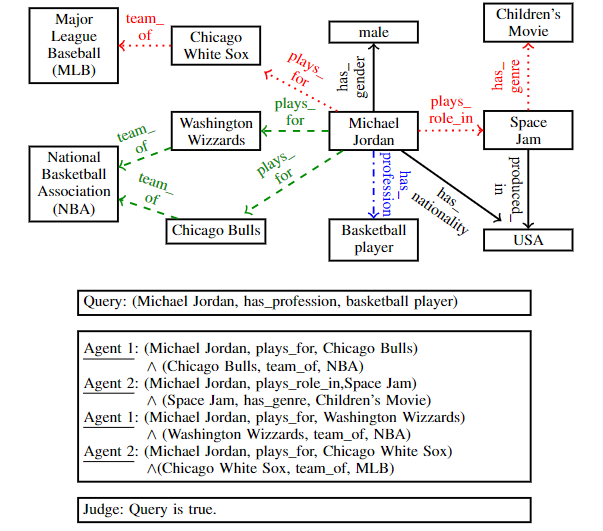
其中$Query$表示论题,$Agent1$持正方论点,即认为迈克尔乔丹是专业篮球运动员,$Agent2$持反方论点,即认为迈克尔乔丹不是专业篮球运动员。双方你来我往,分别搜索到两个最重要的论据,并最终递交给$Judge$进行判决,判决结果为正方论点是正确的,即$Agent1$获胜。
2.2 算法细节
2.2.1 算法基本要素
知识图谱$KG$由节点集合$R$和边集合$E$组成
状态空间($States$,简称$S$,$S_t^{(i)}\in S$),其中$S_t^{(i)}=(e_t^{(i)},q)$,$e_t^{(i)}$表示$Agent(i)$在时刻$t$时所处的位置(节点),$q$表示待查询三元组(即论题,$q=(s_q,p_q,o_q)$)
行动空间($Actions$),$A_{S_t^{(i)}}$表示$Agent(i)$在时刻$t$时下一步可到的节点集合(即$e_t^{(i)}$节点本身及其所有邻节点):$A_{S_t^{(i)}}={(r,e)\in R\times E:S_t^{(i)}=(e_t^{(i)},q)\cap (e_t^{(i)},r,e)\in KG}$
环境($Environments$)与状态转移($\delta_t^{(i)}=(S_t^{(i)},A_t^{(i)}):=(e_{t+1}^{(i)},q)$),当$Agent(i)$在时刻$t$处于状态$S_t^{(i)}$并选择动作$A_t^{(i)}$($A_t^{(i)} \in A_{S_t^{(i)}}$)时,将进行状态的转移(从节点$e_t^{(i)}$移动到了节点$e_{t+1}^{(i)}$)
2.2.2 强化学习策略
策略($Policies$)的选择需要先借助$LSTM$模型进行编码$h_t^{(i)}=LSTM^{(i)}([a_{t-1}^{(i)},q^{(i)}])$,$LSTM$模型的输入项主要包含两部分:
- 时刻$t-1$的动作选择与转移后的状态:$a_{t-1}^{(i)}=[r_{t-1}^{(i)},e_t^{(i)}]$
- 论题在$Agent(i)$对应模型中的嵌入表示:$q^{(i)}=[e_s^{(i)},r_p^{(i)},e_o^{(i)}]$(不同$Agent$或$Judge$间的节点与边的嵌入表示是不一样的,它们会进行独立的更新与学习)
时刻t=0时,$A_o^{(i)}$可以默认为空集,节点与边也都有相同的初始嵌入表示
根据$LSTM$输出的编码信息$h_t^{(i)}$与下一时刻$t$的行动空间$A_t^{(i)}$,可以得到$Agent(i)$在时刻$t$的策略评估向量$d_t^{(i)}=softmax(A_t^{(i)}(W_2^{(i)}ReLU(W_1^{(i)}h_t^{(i)})))$,其中$d_t^{(i)}$的第$k$个分量对应着采取行动空间中第$k$个行动的概率。
假设时刻$t$的动作选择仅与时刻$t-1$的状态有关(无后效性),则策略的选择转变为了一个马尔可夫决策过程,之后策略评估向量$d_t^{(i)}$既可以用于寻找最优策略$A_t^{(i)}$,也可以用于策略的采样
2.2.3 动态辩论机制
对于每一个论题$q=(s_p,p_q,o_q)$都包含真假两种论点$\phi(q)={0,1}$,并分配给正反辩手。设整数$N$作为辩论的回合数,每一方辩手都会在每个回合以节点$s_p$(主语)作为起始点,进行长度为$T$的图遍历(遍历受强化学习策略的指导,也是一个寻找证据链的过程)。对于第$i$的辩手在第$n$个回合寻找到的证据链,公式表示如下:$$\tau_n^{(i)}:=(A_{\widetilde{n}(i,T)+1},A_{\widetilde{n}(i,T)+2},...,A_{\widetilde{n}(i,T)+T})$$ 其中符号$\widetilde{n}(i,T)$的含义是$(2(n-1)+i-1)T$,即一种对索引的重建(reindexing)
最终正反双方(分别对应$i=1$和$i=2$的情况)在$N$轮辩论中搜集到的所有证据链: $$\tau:=(\tau_1^{(1)},\tau_1^{(2)},\tau_2^{(1)},\tau_2^{(2)},...,\tau_N^{(1)},\tau_N^{(2)})$$ 动态辩论的流程伪代码如下:

2.2.4 裁判胜负判定
裁判本质上是一个二元分类器,用于判断双方辩手的胜负;其次裁判还会评估论据的质量,并分配奖励用于指导辩手找到更优地策略用于寻找论据。
具体来说,胜负判断的计算公式是: $$t_\tau=\sigma(w^TReLU(W\Sigma_{i=1}^2\Sigma_{n=1}^Nf([\tau_n^{(i)},q^J])))$$
- 函数$f(\cdot)$表示一个前馈神经网络,用于处理每次输入的证据链信息$\tau_n^{(i)}$和论题信息$q^J$,由上一节可知,证据链$\tau_n^{(i)}$是$T$个策略结果组成的序列
- 对于第$t$次策略的结果$A_t$,本文用$[r_t^J,e_t^J]$的嵌入表示(所有embeding的维度为$d$)组合作为$A_t$的嵌入表示;同理$q^J$的嵌入表示为$[r_p^J,e_o^J]$
- $\tau_n^{(i)}$和$q^J$的维度分别为$2dT$和$2d$,函数$f(\cdot)$的输入维度为$2(T+1)d$,输出维度为$d$
- $2N$条证据链经过函数$f(\cdot)$处理后进行求和,得到对所有证据链的综合信息
- 最后经过两个全连接层得到最终的胜负判断,倒数第二层的权重为$W\in \mathbb{R}^{d\times d}$,激活函数为$ReLU$,最后一层权重为$w\in \mathbb{R}^{d}$,激活函数为$Sigmoid$
裁判的输入信息仅保留了谓语和宾语的嵌入表示,而舍弃了主语,这么做是为了让裁判做出的决定不受主语嵌入表示的影响,而专注于评估论据(考虑到上一轮的宾语会是下一轮的主语,所以唯一被舍弃的只有最初的主语节点$s_p$)
本文作者也尝试过用诸如RNN的复杂网络结构处理证据链,但效果一直不太好
每个论题$q$对应的目标函数(交叉熵损失)为:$$L_q=\phi(q)logt_{\tau}+(1-\phi(q))(1-logt_{\tau})$$ 整体的目标函数(实际训练还包含一个$L_2$正则项)为:$$L=\frac{1}{|\tau|}\Sigma_{q\in \tau}L_q$$ 整体模型结构如下:
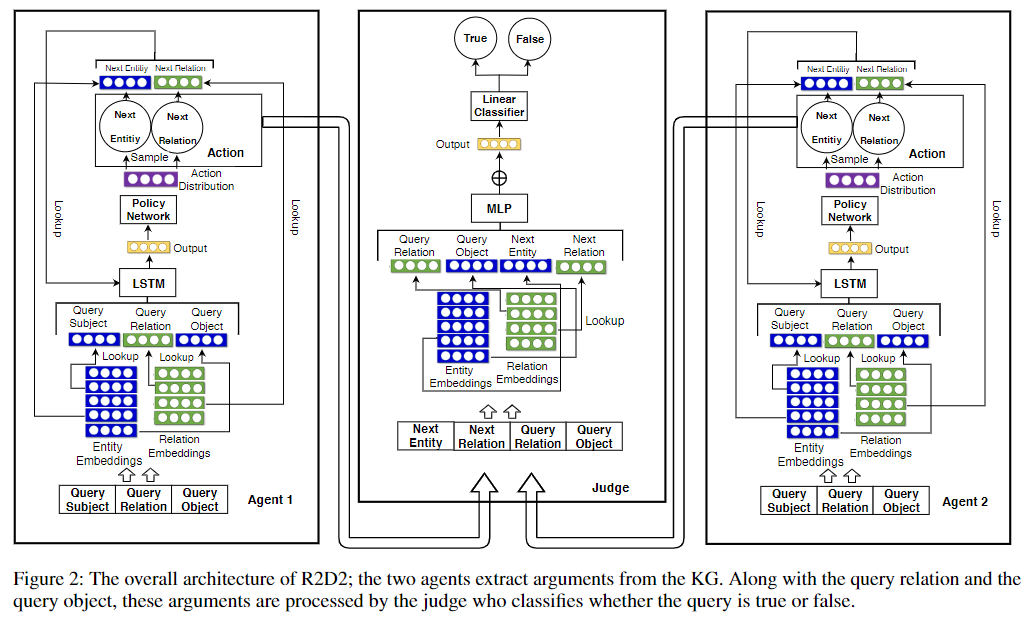
2.2.5 奖惩策略学习
除了对辩手进行胜负判断之外,裁判还需要评估每条证据链的质量用于奖惩辩手,对于$Agent(i)$的第$n$条证据链,其质量评估公式如下: $$t_n^{(i)}=w^TReLU(Wf([\tau_n^{(i)},q^J]))$$
上式中的$w$和$W$沿用了胜负判断中的网络参数值,由于这里的网络参数值是通过论据评估胜负训练得到的,所以上式也自然而然具备了评估论据质量的能力,评估胜负与评估质量之间只差一个$Sigmoid$激活函数(这里的参数复用,妙啊~)
质量的评估结果很容易就可以转化为强化学习的奖励: $$\begin{equation} R_n^{(i)} = \left\{ \begin{array}{rl} t_n^{(i)} & \mbox{if } i = 1, \\ -t_n^{(i)} & \mbox{otherwise} . \end{array} \right. \end{equation}$$
直观理解,找到的论据质量越高,反馈的奖励也就越大
已有的三元组$KG$可以看作事实,并理解为正样本,而训练模型还需要手动构建错误三元组(corrupted triples)作为负面样本集$KG_c$,最终数据集$KG_+=KG\cup KG_c$
通常情况下,负样本会通过随机替换宾语节点的方式构建,但这种方法会产生很多驴头不对马嘴、漏洞百出的负样本。所以作者为了增加挑战性,构建了一些似是而非的高质量负样本用于训练。
高质量负样本的生成方法: $$KG_c:={(s,p,\widetilde{o})|(s,p,\widetilde{o})\notin KG,\exists (s,p,\widetilde{o})\in KG}$$
简单来说,就是本文中的宾语节点不是随机替换的,而是会找和谓语存在关系的宾语进行替换,当然依然需要确保替换后的结果是不存在于原始三元组$KG$中
最后通过最大化累积奖赏的期望,对agent进行训练(强化学习): $$argmax_{\theta(i)}E_{q\sim KG_+}E_{\tau_1^{(i)},\tau_2^{(i)},...,\tau_N^{(i)}\sim\pi_{\theta^{(i)}}}[G^{(i)}|q]$$
- $E_{q\sim KG_+}(\cdot|q)$在训练过程中用训练集上的经验平均值代替,其中$KG_+=KG \cup KG_c$
- $G^{(i)}=\Sigma_{n=1}^NR_n^{(i)}$表示对于$Agent(i)$提出的论据链$\tau_1^{(i)},\tau_2^{(i)},...,\tau_N^{(i)}$的累积奖励
- 学习过程会先训练以下Jundge,然后采用Agent和Jundge交替训练的方式
- 添加正则项参数$\beta \in R_{\leq 0}$,增强算法的探索能力/泛化能力
- 如果想了解强化学习过程中的更多细节,可参阅强化学习的论文原文
2.3 实验分析
数据说明:
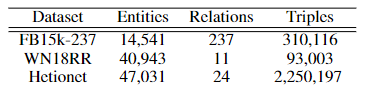
评价指标:
- 针对知识三元组分类任务:准确率Acc、PR AUC、ROC AUC
- 针对知识推理/补齐任务:MRR、平均排名 Mean Rank、TopK 准确率 Hits@K
R2D2的核心是三元组分类问题,比如Judge就是判断知识三元组是否为真。但由于R2D2推理的随机性,因此需要多次推理,并对结果求均值以减少评价的波动性
实验环境:48核CPU+96G内存,每个数据集训练最多耗时4h,测试耗时在1-2h
三元组分类任务的模型对比结果:

知识推理(预测边或节点)任务的模型对比结果:
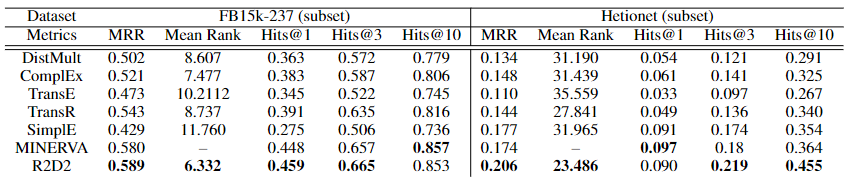
模型的推理结果示例:

其他实验结论概述:
- 调研人类作为Judge时的总体准确率约为81.8%,和R2D2表现比较一致
- 研究发现,对于比较显而易见的论点,Agent有时很难找到对立面的论据
- 刻意遮掩某一方的论据后,最终的Agent判决将是有偏的,这点符合人类直觉