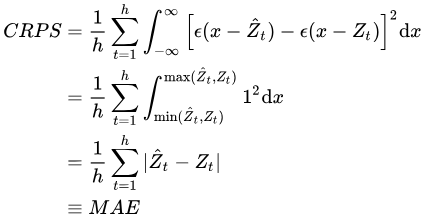模型评价 | Digital Garden

1 分类模型评价指标

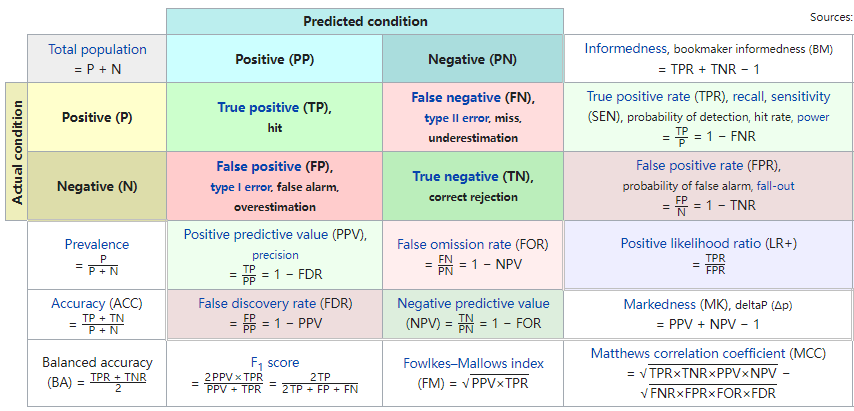
1.1 混淆矩阵

混淆矩阵及其衍生指标：

图源：维基百科-ROC曲线

TP：预测为阳性，实际为阳性 FP：预测为阳性，实际为阴性 FN：预测为阴性，实际为阳性 TN：预测为阴性，实际为阴性

常见相关衍生指标：

准确率（Accuracy，ACC）：模型预测正确的比例

$$(TP + TN) / (TP + TN + FP + FN)$$

灵敏度（Sensitivity）/ 真阳性率（TPR）: 实际阳性样本中预测正确的比例

$$TP / (TP + FN)$$

特异性（Specificity）/ 真阴性率（TNR）：实际阴性样本中预测正确的比例

$$TN / (TN + FP)$$

F1 值（F1 Score）：准确率和召回率的调和平均数，是它们的平衡指标

$$2 \times TP / (2 \times TP+FP+FN)$$

漏诊率（Miss Rate）/ 假阴性率（FNR）: 实际阳性样本中预测错误的比例

$$FN / (TP + FN) = 1 - 灵敏度$$

误诊率（FDR）: 预测为阳性的样本中预测错误的比例

$$FP / (TP + FP)=1-特异度$$

阳性预测值（ PPV）：预测为阳性的样本中实际为阳性的比例

$$TP / (TP + FP)=灵敏度/(1-特异度)$$

阴性预测值（NPV）：预测为阴性的样本中实际为阴性的比例

$$TN / (TN + FN)=(1-灵敏度)/特异度$$

约登指数=灵敏度+特异度-1，常用于指导最佳 cutoff 值的寻找

马修相关系数（MCC，计算公式位于上图右下角）：范围在-1~1之间，1是完美预测，-1是不完美预测，0是随机预测；MCC考虑了混淆矩阵的四个组成部分，可用于分类偏斜的问题

1.2 ROC曲线与AUC

ROC曲线：

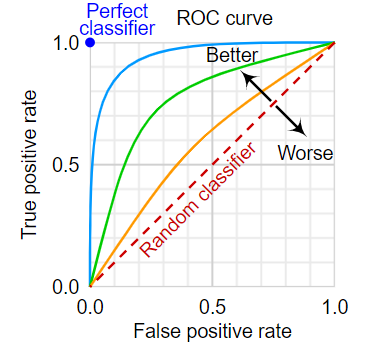
图源：维基百科-ROC曲线

AUC（Area Under Curve）被定义为ROC曲线下与坐标轴围成的面积，取值范围在0.5和1之间。

AUC越接近1.0，意味着模型效果越好。

1.3 PR曲线与AUPRC

与ROC曲线原理类似，只不过横坐标换为Recall，纵坐标换为Precision。最终得到的曲线下与坐标轴围成的面积，也就被称为AUPRC了

1.4 kappa值

Kappa值常用于一致性检验的指标，也可以用于衡量分类的效果（即衡量预测类别与实际类型的一致性），Kappa值的计算也依赖于混淆矩阵： $$Kappa=\frac{p_o-p_e}{1-p_e}$$ 其中$p_o$表示模型的分类准确度： $$p_o=\frac{\Sigma_{i=1}^kn_{ii}}{N}$$ 而$p_e$表示随机分类的准确度： $$p_e=\frac{\Sigma_{i=1}^k[\Sigma_{j=1}^kn_{ij}\times\Sigma_{i=1}^kn_{ji}]}{N^2}$$ 其中$N$表示矩阵元素之和，也可以理解为测试集的样本量。$k$表示矩阵的行数与列数，也可以理解为分类模型的分类类别数。

对于二元分类问题，Kappa值的计算可以简化如下： $$Kappa=\frac{2\times (TP\times TN-FN\times FP)}{(TP+FP)\times (FP+TN)+(TP+FN)\times (FN+TN)}$$ Kappa的公式含义可解释为： $$Kappa=\frac{modelAccuracy-randomAccuracy}{1-randomAccuracy}$$ 其中分子描述的是当前模型准确度相对于随机准确度的提升度，而分母描述的是完美模型相对于随机准确度的提升度。一般来说当类别不平衡时，$p_e$也就越高，kappa值越低，因此kappa值能够避免类别不均衡问题导致的评价偏见

$p_e$计算示例（方便理解）：

假设总共有三个类别$L_1,L_2,L_3$，对应的真实样本数分别为$a_1,a_2,a_3$

通过模型预测得到每个类别的预测样本数分别为$b_1,b_2,b_3$

设总样本数为$n$，则类别$L_1$中预测值与真实值匹配的概率为$\frac{a_1}{n}\times \frac{b_1}{n}$

以此类推，随机预测的综合准确度$p_e=\frac{a_1\times b_1 +a_2\times b_2 + a_3\times b_3}{n\times n}$

Kappa值的取值范围是-1到1，但一般在0-1之间，Kappa值越接近1，表明两种分布之间的一致性越高，也意味着模型分类效果越好

QWK（quadratic weighted kappa），又称Cohen's kappa。是一种适用于评价多分类任务的二次加权kappa，应用较为广泛；当QWK大于0.85时，一般就认为模型较好（一致性高）

1.5 多分类精度

宏平均（macro-averaging）：单独计算每个类别的相应指标，然后取平均

宏精确率（Macro-Precision）：$P_{macro}=\frac{1}{n}\Sigma_{i=1}^nP_i$
宏召回率（Macro-Recall）：$R_{macro}=\frac{1}{n}\Sigma_{i=1}^nR_i$
宏F值（Macro-F Score）：$(2\times P_{macro}\times R_{macro})/(P_{macro}+R_{macro})$

微平均（micro-averagin）：建立全局混淆矩阵，然后计算相应的指标

微精确率（Micro-Precision）：$P_{micro}=(\Sigma_{i=1}^nTP_i)/(\Sigma_{i=1}^nTP_i+\Sigma_{i=1}^nFP_i)$
微召回率（Micro-Recall）：$R_{micro}=(\Sigma_{i=1}^nTP_i)/(\Sigma_{i=1}^nTP_i+\Sigma_{i=1}^nFN_i)$
微F值（Micro-F Score）：$(2\times P_{micro}\times R_{micro})/(P_{micro}+R_{micro})$

以上指标仅考虑的平均值的情况，实际场景还可以根据需求进行类别/样本的加权

宏平均（macro-averaging） vs 微平均（micro-averagin）

宏平均假设每个类别之间是等权重的，相对更重视小样本的类别；微平均假设每个样本之间是等权重的，相对更重视大样本的类别；二者都有各自的特点，不存在孰优孰劣的问题

2 回归模型评价指标

相关符号说明：

$n$：样本数 $k$：特征数 $y$：真实值 $\overline{y}$：真实值均值 $\hat{y}$：预测值

2.1 常见误差类指标

均方误差（mean square error，MSE）： $$MSE=\frac{1}{n}\Sigma_{i=1}^n(y_i-\hat{y}_i)^2$$

平均绝对误差（mean absolute error，MAE）： $$MAE=\frac{1}{n}\Sigma_{i=1}^n|y_i-\hat{y}_i|$$

均方根误差（root mean square error，RMSE）： $$RMSE=\sqrt{\frac{1}{n}\Sigma_{i=1}^n(y_i-\hat{y}_i)^2}$$

均方根对数误差（root mean square log error，RMSLE）： $$RMSLE=\sqrt{\frac{1}{n}\Sigma_{i=1}^n[log(y_i+1)-log(\hat{y}_i+1)]^2}$$

注意：

以上误差类指标对于回归模型来说，都是越小越好，最小值可以接近0

误差类指标存在量纲差异，因此可能存在一种降低另一种反而增加的可能

带有平方计算的指标对异常值更敏感，带有绝对值的指标计算时更麻烦

其他误差类指标（后补充）：

平均百分比误差（mean percentage error，MPE）
$$MPE=\frac{1}{n}\Sigma_{i=1}^n[(y_i-\hat{y}_i)/y_i]$$
平均绝对百分比误差（mean absolute percentage error，MAPE） $$MAPE=\frac{1}{n}\Sigma_{i=1}^n|(y_i-\hat{y}_i)/y_i|$$

2.2 拟合优度及其修正

拟合优度/决定系数（Goodness of Fit，$R^2$）: $$R^2=\frac{SSR}{SST}=1-\frac{SSE}{SST}=1-\frac{\Sigma_{i=1}^n(y_i-\hat{y}_i)^2}{\Sigma_{i=1}^n(y_i-\overline{y}_i)^2}$$

其中：

$SSE$（explained sum of squares，又称$ESS$）表示模型预测到的可解释变动
$SSR$（residual sum of squares，又称$RSS$）表示模型未预测到的未知变动
$SST$（total sum of squares，又称$TSS$）表示总体变动，为前两者之和

特征越多，模型的拟合优度越大，因此需要借助自由度对拟合优度进行修正： $$R^2_{adjusted}=1-\frac{SSE/(n-k-1)}{SST/(n-1)}$$

伪拟合优度/决定系数（Pseudo-R-squared）：当结果变量是名义变量或序数变量时，原本的R^2就不能作为拟合优度，而是需要使用伪拟合优度，常见的伪拟合优度可参阅wiki-Pseudo-R-squared

3 模型稳定性评价指标

线性模型的稳定性：3 多重共线性相关指标

群体稳定性指标（Population Stability Index，PSI）

4 推荐排序模型评价指标

分类模型的评价指标也可以用于推荐排序任务

对于类别数较多或精度要求不高的分类任务也可以使用排序模型的评价指标

4.1 MRR

平均倒数排名（Mean Reciprocal Rank, MRR）：根据推荐结果中正确结果的排名，来评估整个推荐系统的性能

计算示例：最终的MMR值=(1/3 + 1/2 + 1)/3 = 11/18

图源：wikipedia-Mean reciprocal rank

4.2 TopK相关指标

P@K：top-k 推荐中存在多少相关项目

AP@K：P@1、P@2 ... P@K的平均值，通常是针对单用户计算的

MAP@K：所有用户的 AP@K 的平均值

Recall@K ：用户实际交互的 top-k 项目中被推荐的项目占比

5 概率输出评价指标

5.1 CRPS

$${\rm{CRPS}}={\int }_{-{\rm{\infty }}}^{+{\rm{\infty }}}\left[F^f\left(y\right)-F^o\left(y\right)\right]^2{\rm{d}}y$$

其中$F^f$表示预测分布的累积分布函数（CDF）， $F^o$表示真实观测值的CDF
当预测分布与真实分布完全一致时，CRPS 为零
预测分布过于集中、过于分散，亦或是偏离观测值太远都会导致 CRPS 增大

由于一般情况下真实观测值都是单独的，不会是一个概率分布（除非堪破量子力学或多元宇宙）

因此常使用以下公式代替原始公式进行近似计算： $${\rm{CRPS}}=\frac{1}{n}\Sigma_{t=1}^h{\int }_{-{\rm{\infty }}}^{+{\rm{\infty }}}\left[F^f\left(x\right)-\epsilon \left(y-\hat{y}\right)\right]^2{\rm{d}}x$$ 其中$\hat{y}$为真实观测值，$\epsilon$为单位跃迁函数（输入小于0时输出0，否则输出1）

CRPS 也可以看作是点预测中常见的 MAE 指标的泛化：

6 NLP模型评价指标

6.1 BLEU

BLEU（bilingual evaluation understudy） $$BLEU=exp(min(0,1-\frac{len_{label}}{len_{pred}}))\Pi_{n=1}^kp_n^{1/2^n}$$

$len_{label}$表示标签序列中的词元数
$len_{pred}$表示预测序列中的词元数
$exp(min(0,1-\frac{len_{label}}{len_{pred}}))$作为惩罚项，避免预测序列远短于标签序列的情况
$k$是用于匹配的最长的$n$元语法
$p_n$表示$n$元语法的精确度，它是两个数量的比值：分母是预测序列中$n$元语法的数量，分子是预测序列与标签序列中匹配的$n$元语法的数量
$1/2^n$是针对$p_n$权重，$n$越大时对应的$p_n$越重要

BLEU常用于衡量机器翻译质量，取值范围是[0, 1]，越接近1表明翻译质量越好

6.2 ROUGE

ROUGE指标是在机器翻译、自动摘要、问答生成等领域常见的评估指标

ROUGE指标常通过对比生成文本与参考答案来进行计算，常用计算方式有4种：

ROUGE-N：将BLEU的精确率优化为召回率 $$Rouge_N=\frac{\Sigma_{TEXT}\Sigma_{gram_n \in TEXT}Count_{matched}(gram_n)}{\Sigma_{TEXT}\Sigma_{gram_n \in TEXT}Count(gram_n)}$$
ROUGE-L：将BLEU的n-gram优化为最长公共子序列（LCS） $$\begin{equation} \left\{ \begin{gathered} R_{LCS}=\frac{LCS(C,S)}{len(S)} \ \\ P_{LCS}=\frac{LCS(C,S)}{len(C)} \ \\ F_{LCS}=\frac{(1+\beta^2)R_{LCS}P_{LCS}}{R_{LCS}+\beta^2P_{LCS}} \end{gathered} \right.

\end{equation}$$

ROUGE-W：针对ROUGE-L中存在的连续匹配情况，给予更高的奖励
ROUGE-S：不要求n-gram是完全连续的，允许出现跳词(skip)

ROUGE指标分析：

只能在单词、短语的角度去衡量两个句子的形似度
并不能支持同义词、近义词等语意级别去衡量

ROUGE指标与BLEU指标非常类似，均可用来衡量生成结果和标准结果的匹配程度

不同的是ROUGE基于召回率，BLEU更看重准确率

7 其他模型评价指标

7.1 学习曲线

学习曲线（Learning Curve）常用于评估数据量和模型训练是否过拟合

一般横轴为数据量/训练次数，纵轴为模型性能-准确率/预测误差
学习曲线能直观地判断数据量/训练次数增加对模型性能的影响
根据训练集和验证集的学习曲线差异可以评估模型是否过拟合

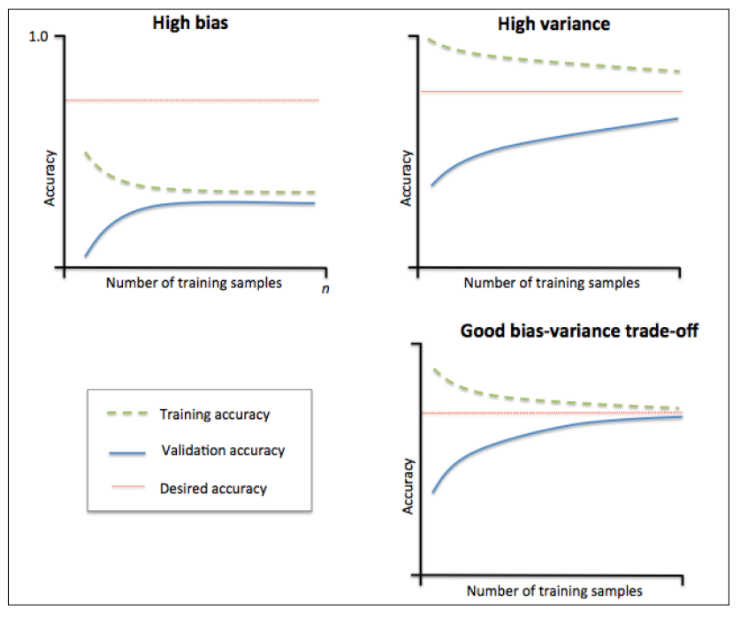
其中High bias表示高偏差，此时是欠拟合，可以构建更多特征、增加模型复杂度、减弱正则项
其中High variance表示高方差，此时是过拟合，可以增大训练集、降低模型复杂度、加强正则项

7.2 决策曲线

决策曲线分析（Decision Curve Analysis）在确定阈值概率的情况下，分析预测因子对应临床决策的净收益

以癌症预测场景为例，其对应的临床决策可以是”进行活组织检查“

较低的阈值概率意味着更关注对事件的风险（患者担心癌症）
较高的阈值概率意味着更关注对临床决策的风险（患者反对活检）
当阈值概率设定为10%，说明医生认为早期发现癌症的效用是避免不必要的活检危害的 9 倍

净收益的计算公式： $$Net\ Benefit=\frac{True\ positives-False\ positives\times \frac{p_t}{1-p_t}}{N}$$

其中$p_t$表示阈值概率，其他变量均为计数统计
净收益为真假阳性的加权组合，权重根据阈值概率确定

决策曲线横轴为阈值概率，纵轴为净收益：

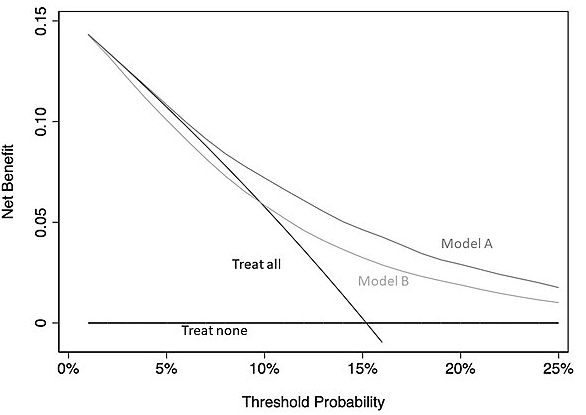
其中Treat all对应实线表示全都进行临床决策（活检）的策略净收益
其中Treat none对应实线表示全都不进行临床决策（活检）的策略净收益
当预测风险低于5%的情况下，选择活检是不合理的（净收益低于Treat all对应实线）
当预测风险高于25%的情况下，拒绝活检是不合理的（绝对净收益过低）
上图中的最优模型是Model A，因为其在5-25% 的阈值概率范围内具有最高净收益

决策曲线适用于二分类模型，或其他模型输出结果为风险百分比的情况

7.3 校准曲线

校准曲线（Calibration Curve）观察分类模型的预测概率是否接近于经验概率(指的是真实概率)

绘制步骤：

通过分桶法(分桶策略分为‘uniform’, ‘quantile’)对预测概率进行数据离散化
求出每个桶里面所有样本预测概率的平均值，作为横坐标
求出每个桶里面正例的占比，作为纵坐标（真实概率）

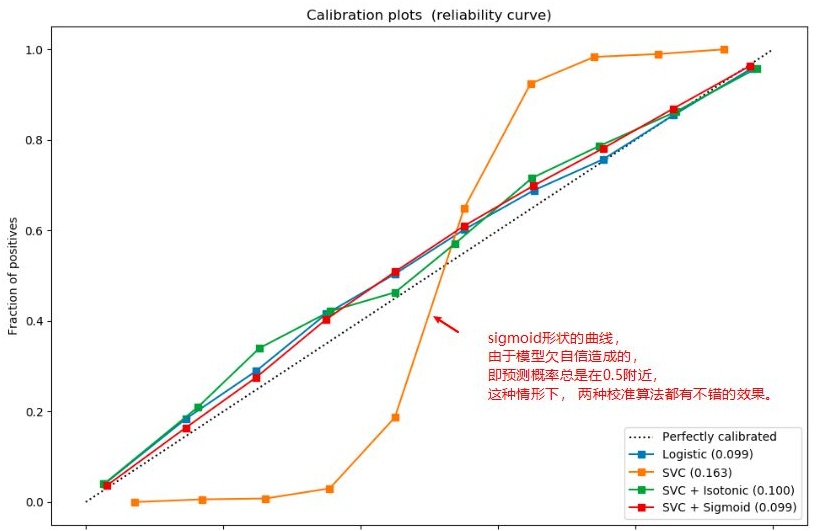
校准曲线评估的是预测概率与真实概率的一致性
当校准曲线越接近于一条对角线，说明模型一致性高
缺乏自信的模型的校准曲线是sigmoid形状，此时可以用Isotonic/Sigmoid算法进行校准
过度自信的模型的校准曲线是反gmoid形状，此时只能用Isotonic算法进行校准

7.4 bland Altman

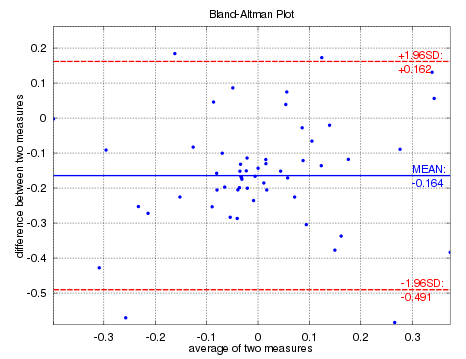
Bland –Altman 图（差异图）是一种数据绘图方法，用于分析两种不同测定之间的一致性