1 数据偏斜概述
又称为数据不平衡(imbalanced)问题,指分类任务中不同类别之间的样本数差异过大的情况。数据偏斜常见于医疗诊断、文本分类、金融欺诈、异常检测等领域,一般认为样本比例大于4:1时,便存在样本不平衡的问题,一些极端的场景下,会存在1000:1的样本比例,甚至一个类型只有一个样本的情况
数据偏斜问题的影响:干扰建模过程,错误地学习到样本分布等先验信息,使得模型结果的预测存在偏见(倾向于预测出现频次更高的类别)
数据偏斜问题的解决:一般从数据、算法、损失函数和评估指标四个角度入手
2 解决不平衡-重抽样
重抽样实则是一种无奈之举,如果能直接对少数类样本直接补充数据其实是最合适的
重抽样方法的核心原则:去重冗余和存在杂质的样本,保留并拓展具备代表性的样本
2.1 欠采样
欠采样:减少占比过高类型的样本量,欠采样时注意保留具备独特性的样本,剔除的样本也最好是信息相对冗余的,这样能避免类别内信息的损失
欠采样常用方法:随机欠采样、Cluster Centroids、NearMiss、Tomek links、Edited Nearest Neighbors(ENN)、Repeated Edited Nearest Neighbours(RepeatedENN)、AIIKNN、Condensed Nearest Neighbor(CNN)、One-Sided Selection、Neighborhood Cleaning Rule、Instance Hardness Threshold
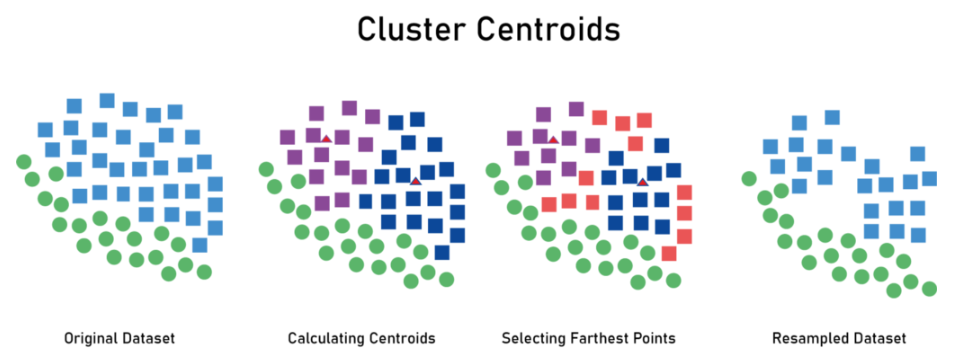
2.1.1 算法细节:Cluster Centroids
核心思想:借助聚类保留最核心的关键样本
Cluster Centroids算法步骤:
- 设定K值(聚类的类别数),然后对多数类样本进行聚类
- (方法1)剔除距离所有聚类质心都较远的边缘样本
- (方法2)根据聚类质心合成新的样本
算法分析:
- 可以直接控制最终欠采样的数量
- 有时需要设置较大的K值,计算成本偏高
- 方法2属于欠采样比较少见的生成型方法,一般都是筛选型方法
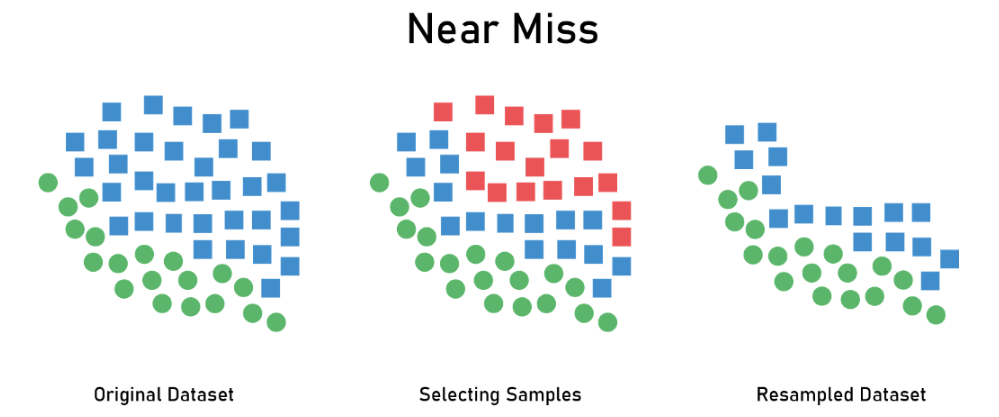
2.1.2 算法细节:NearMiss
核心思想:距离少数类样本较远的多数类样本相对来说没那么重要
NearMiss算法步骤:
- NearMiss-1:计算每个多数类样本与最邻近的$n$(默认为3)个少数类样本的平均距离,然后选择保留最近的$K$个多数类样本
- NearMiss-2:计算每个多数类样本与最远的$n$(默认为3)个少数类样本的平均距离,然后选择保留最近的$K$个多数类样本
- NearMiss-3:针对每个少数类样本,计算与多数类样本的距离,保留最近的$M$个多数类样本
- NearMiss-3(STEP2-可选):计算所有剩余多数类样本与最邻近的$n$(默认为3)个少数类样本的平均距离,然后选择保留最远的$K$个多数类样本
算法分析:
- NearMiss-1计算距离时考虑最邻近的少数类样本,容易受到数据噪声的影响
- NearMiss-2计算距离时考虑最远的少数类样本,相比于NearMiss-1更不容易受到数据噪声的影响,但依然可能受到边缘异常值的影响,是三个方法中综合表现最好也最常用的
- 由于NearMiss-3先根据少数类样本进行了多数类样本的筛选,所以相比于NearMiss-1和NearMiss-2,计算开销更小且不容易受到数据噪声的影响,但也引入了额外的超参数
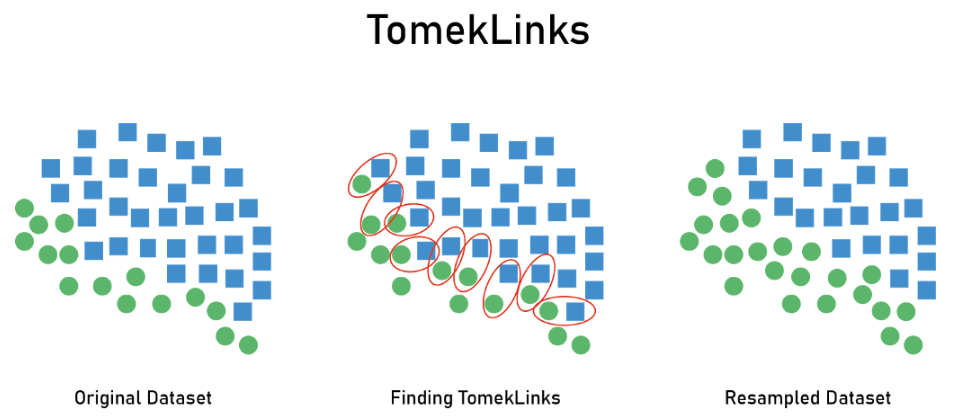
2.1.3 算法细节:Tomek links
核心思想:剔除最邻近属于少数类样本的多数类样本
Tomek links算法步骤
- 遍历样本,寻找归属于不同类且距离最近的样本对(Tomek link)
- 剔除这些样本对中属于多数类的样本(可选:删除其中的少数类样本)
算法分析
- 剔除了大量存在噪声的数据,虽然可能存在信息的丢失
- 常作为一种补充方法与其他方法(比如SMOTE)配合使用
2.1.4 算法细节:ENN
核心思想:剔除周围少数类样本过多的多数类样本
ENN算法步骤:
- 遍历多数类样本,计算距离最近的$K$个样本
- 其中属于多数类样本的有$a$个,属于少数类样本的有$b$个
- 设定阈值参数$\alpha$(常用值为0.5),舍弃$a/(a+b)<\alpha$的样本
算法分析:
- 阈值参数$\alpha$较大时,筛选结果更激进,筛掉的样本更多
- 阈值参数$\alpha$较小时,筛选结果更保守,筛掉的样本更少
ENN算法变种
- RepeatedENN通过重复运行ENN算法,实现了更多样本的筛除
- AllKNN在重复运行ENN算法时,会逐步增加邻接样本数$K$
2.1.5 算法细节:CNN
核心思想:借助1-邻近分类器(1-NN)保留容易预测错误的样本
CNN算法步骤:
- 构建集合$C$,包含所有少数类样本和随机的一个多数类样本
- 构建集合$S$,包含剩余的所有多数类样本
- 根据集合$C$训练并构建1-邻近分类器(1-NN)
- 利用1-NN依次预测集合$S$中的样本,将预测结果与实际不一致的样本从集合$S$移到集合$C$中并重新训练1-NN。重复以上过程,直至1-NN在集合$S$中不再有预测错误的样本
算法分析:
- 对数据噪音较为敏感,并且可能导致更严重的样本噪音
CNN算法变种
- 适合与TomekLinks配合使用,也就得到了OneSidedSelection抽样算法
- Neighborhood Cleaning Rule会融合ENN和CNN,保留两个算法最终筛选结果的并集
2.1.6 算法细节:Instance Hardness Threshold
核心思想:用分类器在数据上训练,并去除概率较高的样本
算法分析:
- 可拓展性强,接受scikit-learn内置的所有分类器
- 由于是通过概率阈值筛选,最终的筛除样本量不能确定
2.2 过采样
过采样:增加占比过低类型的样本量,过采样时简单地复制样本容易导致模型的过拟合。实际操作时可以借鉴人类先验知识(比如图像的翻转、调色等)进行数据增强,也可以捕捉原样本的分布信息进行样本的丰富,但要注意避免引入不必要的噪声,导致模型精度的下降
过采样常用方法:随机过采样、SMOTE、Borderline SMOTE、SVM SMote、k-Means SMOTE、ADASYN(Adaptive Synthetic)、其他常见数据增强技术
实际应用中,欠采样和过采样可以搭配使用(比如SMOTE+ENN)
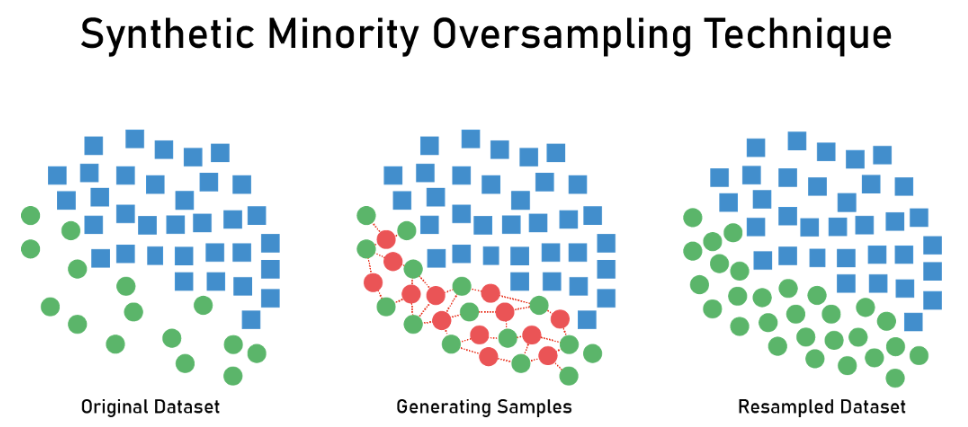
2.2.1 算法细节:SMOTE
核心思想:选取特征空间中距离较近的同类样本,通过插值的方式构建新样本
SMOTE算法步骤:
- 针对样本$X$,寻找距离最近的$K$个同类样本,并从中随机抽一个样本$X_k$
- 根据以下插值方法生成基于新样本:$x_{new}=x+(x_k-x)\times \delta ;\delta \in [0,1]$
- 设定采样倍率$N$,每个样本重复以上过程$N$次,合成$N$个新样本
算法分析:
- 可能会在两个异常值间插值,引入额外的信息噪声
- 模糊了分类样本的边界,增大了模型的分类难度
- 样本是等权重的,没有区分easy和hard样本
SMOTE算法变种:
- 修改距离计算方法,比如SMOTEN使用VDM计算分类型变量的距离;SMOTENC可以适用于混合型(分类型+数值型)变量的距离计算
- 将插值改为其他的样本生成方法,比如SVM SMOTE使用SVM寻找支持向量并用于新样本的生成;KMeansSMOTE根据聚类密度生成新的样本
2.2.2 算法细节:ADASYN(自适应合成采样)
核心思想:和SMOTE算法类似,但引入了权重机制,重视混淆区域的少数类样本
ADASYN算法步骤:
- 针对样本$X$,寻找距离最近的$K$个样本
- 其中属于多数类样本的有$a$个,属于少数类样本的有$b$个
- 将$a/(a+b)$作为样本的权重,周围异类样本越多越受重视
- 权重越高的样本会通过插值(过程同SMOTE算法)生成更多的新样本
算法分析:
- 容易在两类样本的接壤边界区域生成过多样本
- 引入过多的信息噪声,加重了模型的分类难度
2.2.3 算法细节:Borderline-SMOTE
核心思想:部分少数类样本可能属于离群点,周围存在多数类样本较多的情况,对这种少数类样本进行过采样容易引入额外的噪音。同理,对周围完全没有多数类样本的少数类样本进行过采样的必要性也不算太强
Borderline-SMOTE算法步骤:
- 针对样本$X$,寻找距离最近的$K$个样本
- 其中属于多数类样本的有$a$个,属于少数类样本的有$b$个
- 设定阈值参数$\alpha$,舍弃$a/(a+b)>\alpha$的样本
- (可选)设定阈值参数$\beta$,舍弃$a/(a+b)<\beta$的样本
- 对剩余样本进行插值生成新样本(过程同SMOTE算法)
在使用BorderlineSMOTE函数时,参数kind存在两种取值 :'borderline-1'或者'borderline-2'。区别在于,用Borderline-1时,构造插值临近点必须是同类的。用Borderline-2时,插值点可以是所有类别的。
算法分析:
- 相比ADASYN,一定程度上降低了可能引入的信息噪声
- 相比SMOTE,对easy和hard样本进行了区分与取舍
3 解决不平衡-算法选择
3.1 集成学习
集成学习:借助局部信息训练多个弱学习器,并借助集成的思想构建出强学习器。这种训练方式天然地对数据偏斜问题不敏感,也很容易借助这种方法对已有算法进行拓展
基于集成学习思想的常用拓展:EasyEnsemble、BalanceCascade、Self-paced Ensemble、MESA(Meta-sampler)
由于大部分集成学习都是基于采样策略去构建弱学习器,并进行集成,所以本小节提到的继承策略都可以去之前的采样策略进行融合(因此集成学习可以看作不损失信息的欠采样,实现了普通欠采样的上位替代,所以集成学习和过采样策略融合的情况更常见)
集成算法的相关知识可参阅:集成算法
3.1.1 算法细节-EasyEnsemble
EasyEnsemble算法步骤:
- 将多数类样本随机划分成n份,每份的数据等于少数类样本的数量
- 对这n份数据分别训练基/弱学习器,最后集成得到强学习器结果
- 集成的常见方法包括:均值法、投票法、学习法(stacking)
算法分析:
- 与集成算法中的bagging类算法(比如随机森林)类似
- 弱学习器的模型有很多选择,拓展能力强
- 训练速度快、对缺失值不敏感,泛化能力强
- 面对噪声较大的样本容易过拟合,拟合能力一般
3.1.2 算法细节-BalanceCascade
这类算法采用了有监督结合boosting的方式
- 第一轮,从多数类中抽取子集与少数类样本联合起来训练模型
- 在下一轮中丢弃此轮被正确分类的样本,并重新进行抽样与训练
- 重复以上过程,使得后续的基学习器能够更加关注那些被分类错误的样本
- 最后集成模型结果(均值法、投票法、学习法)
算法分析:
- 继承了EasyEnsemble算法的优势,同时拟合能力更强
- 对异常样本敏感,容易影响到后期迭代的弱学习器
3.1.3 算法细节-Self-paced Ensemble
Self-paced Ensemble在欠采样+集成策略(boosting)的基础上引入了分桶机制、分类硬度函数(Classification Hardness Function)和自步因子$\alpha$,对算法进行了更优雅的实现
分类硬度函数:任何可分解到单个样本上计算的损失/误差函数都可以被用作分类硬度函数(比如Absolute Error/MSE/Cross-Entropy)
Self-paced Ensemble算法伪代码实现:

Self-paced Ensemble算法步骤:
- 对多数类样本进行欠采样,并训练$n$个弱学习器$f$,平均法集成得到初始强学习器$F_0$
- 基于强学习器预测值和硬度函数对多数类样本进行分桶,确保不同桶内的样本硬度总和一致,并在后续的动态更新中尽量保持桶间的硬度均衡
- 自步因子$\alpha$会在迭代过程中逐渐增大,抑制容易分类样本的抽样概率。假设第$t$个桶的平均样本硬度为$h_t$,则该桶的采样权重为$\frac{1}{h_t+\alpha}$(后续还会进行归一化)
补充说明:桶的采样权重并不等价于桶内样本的采样概率,而是决定了桶内采样数
假设样本量高而平均硬度低的桶为$B_1$,样本量低而平均硬度高的桶为$B_2$。在迭代初期,自步因子$alpha$比较小,桶的权重正比于桶内平均硬度的倒数,即桶$B_1$的权重大于$B_2$。随着自步因子$alpha$的增大,每个桶的权重将趋于一致,权重决定了每个桶的最终采样数,所以桶$B_1$和桶$B_2$最终采样数将趋近一致,即桶$B_1$内的样本采样概率小于桶$B_2$
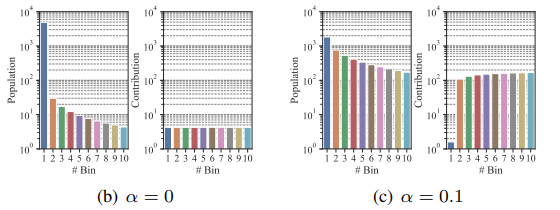
上图展示了不同$\alpha$值对采样权重的影响,其中Population表示每个桶内样本数,Conrtribution表示每个桶中样本的硬度贡献(也对应着样本最终的采样概率)
Self-paced Ensemble算法分析:
- 分桶采样缓解了单个离群样本对模型的影响,提高了模型的稳健性
- 自步因子用一种更优雅的方式提高了模型对于易分错样本的关注度
- 算法对超参数的选择不敏感,不过$k$值过小的话会降低模型的性能
- 对于样本硬度的计算引入了额外成本,不过作者有进行代码上的优化(但是对于KNN、神经网络等模型,依然会存在一定的额外计算成本)
本小节部分内容参考自论文原作者在知乎中对于此算法的解读
3.1.4 算法细节-MESA
通过元学习的思想直接构建权重的生成模型,比如Meta-weight-net就是针对神经网络模型设计的元学习器(输入为样本损失,输出为样本权重)。而MESA可以看作一种更通用集成学习架构,将集成模型的训练和采样器的训练进行解耦:
MESA算法细节:
- 采样器多采用神经网络类结构,输入为预测误差分布(硬度分布)等与任务无关(意味着在不同任务中是通用的)的状态信息,输出为采样策略,优化策略为强化学习
- 针对每个样本,采样器输出采样概率,针对采样后数据训练一个基学习器并加入集成模型,完成一次模型的更新并构建新的状态信息传入采样器,生成下一次的采样策略
MESA算法分析:
- 通用性强,适合不同类型的基学习器,每一个环节都可以分别优化改进
- 由于采样器与集成模型是解耦的,所以采样器可以迁移到不同的任务中
3.2 异常检测
异常检测:对于样本比例严重失衡的情况,可以考虑将分类问题转化为异常检测问题
异常检测常用方法:统计检验、one-class SVM、Isolation Forests、Minimum Covariance Determinant、Local Outlier Factor
3.3 深度学习
伴随着深度学习的兴起,数据偏斜问题的处理出现了新的解决方向。
- 迁移学习借助通用性网络的学习能力迁移,实现了对小样本问题的更好处理
- 自监督或半监督学习,小样本学习,能够在样本量较少的情况下实现良好建模
- 对抗式学习与其他深度学习相关的数据增强技术,为过采样提供了很多新思路
- 元学习(meta-learning)将采样策略的自适应生成融入到神经网络中
4 解决不平衡-代价敏感
通过合理地修改损失函数或算法迭代过程,可以增强模型对于少样本类型的重视程度(增加权重/加大错误时的惩罚),这类方法也可以用于增加模型对于易分错的难样本的重视程度,从而改善模型的学习效果
具备调整不同错误分类成本的算法,也被称为成本/代价敏感算法。常见的成本/代价敏感算法包括:逻辑回归、决策树、支持向量机、神经网络、树集成类
常用的损失函数改进方法:Focal loss、GHM(Gradient Harmonizing Mechanism)、OHEM(Online Hard Example Mining)
常见的代价敏感改进算法:CS-SVM、FSVM-CIL
4.1.1 算法细节-Focal loss
原始二分类任务的交叉熵(Cross entropy)可表示如下: $$L_{CE}= \begin{equation} \left\{ \begin{gathered} -log(p),\ if\ \ y=1 \ \\ -log(1-p),\ if\ \ y=0 \end{gathered} \right. \end{equation}$$ 而针对不平衡任务改进后的 Focal loss 可表示如下: $$FocalLoss= \begin{equation} \left\{ \begin{gathered} -\alpha(1-p)^\gamma log(p),\ if\ \ y=1 \ \\ -(1-\alpha)p^{\gamma}log(1-p),\ if\ \ y=0 \end{gathered} \right. \end{equation}$$ Focal loss的主要改动有以下两点:
- 增加了超参数$\alpha$用于衡量类别的权重,默认值为$0.2$
- 增加了超参数$\gamma$用于对高置信样本进行打压,默认值为$0.25$
Focal loss分析:
- 增强了模型对少样本类与难分类样本的重视程度
- 实现简单,超参数方便调整,实践效果较好
- 最终模型容易受到离群异常值的影响
4.1.2 算法细节-GHM
核心思想:在Focal loss的基础上继续优化,减弱离群点对模型的影响
GHM算法细节:
- 引入梯度模长$g$表示每个样本预测概率与真实值的差值(恒为正数)
- 构建梯度密度函数$GD(g)$,即梯度模长$g$在区间$(g-\frac{e}{2},g+\frac{e}{2})$内数量除以区间长度
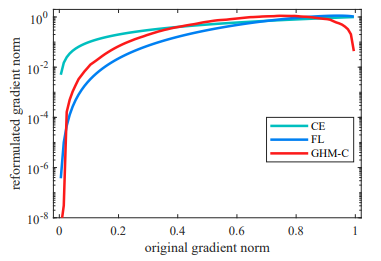 上图中,横坐标表示梯度模长$g$,纵坐标表示权重。梯度模长接近0的部分表示易分类样本,接近1的部分表示难分类样本,可以看到GHM算法对两端都有一定的抑制作用
上图中,横坐标表示梯度模长$g$,纵坐标表示权重。梯度模长接近0的部分表示易分类样本,接近1的部分表示难分类样本,可以看到GHM算法对两端都有一定的抑制作用
最终的GHM损失函数定义如下: $$L_{GHM}=\Sigma_{i=1}^N\frac{L_{CE}(p_i,p_i^{\ast})}{GD(g_i)}$$ 其中$N$表示总样本数,$p_i$表示真实概率,$p_i^*$表示真实标签
5 用于不平衡数据的评估指标
其中对正负样本比例不敏感的评估指标包括:AUC、AUPRC、Kappa
6 扩展阅读
awesome-imbalanced-learning:包含数据不平衡学习相关的框架、论文汇总
imbalanced-learn:专注于不平衡学习的Python模块
imbalanced-ensemble:专注于不平衡集成算法的Python模块
Machine Learning Mastery文章存档-不平衡学习
7 参考资料
图片参考-Resampling to Properly Handle Imbalanced Datasets in Machine Learning