17.极坐标的二重积分及其应用
发表评论
868 views

1 极坐标的二重积分

例题：计算二重积分$\int\int{1-x^2-y^2}dA$，限定区域在$x^2+y^2<1,x\geq 0,y\geq 0$

分析：考虑$sin^x+cos^2=1$的特性，极坐标化将极大简化运算过程

  1. 对变量进行极坐标化，带入$x=rcos\theta,y=rsin\theta$
  2. 对函数图像进行网格化处理，在笛卡尔坐标系中，函数区域将会细分为多个横平竖直的小矩阵；而在极坐标系中，函数区域将有无数从原点出发的射线与半径不一同心圆（具体结果如下图所示）
  3. 此时很明显$dr\cdot d\theta \neq dA$，并且根据面积近似计算可得$dA=rdrd\theta$
  4. 定义积分顺序为先$r$后$\theta$，所以原二重积分转化为$\int_0^{\frac{\pi}{2}}\int_0^1(1-r^2)rdrd\theta =\frac{\pi}{8}$

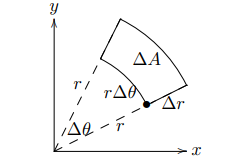
2 极坐标的二重积分应用

  1. 应用1：求给定区域R的面积，此时被积分函数为1： $$Area(R)=\int \! \! \! \int_R(1)dA$$ 当被积分函数为密度函数$\delta$时，积分结果为质量$M=\int!!! \int_R\delta dA$

  2. 应用2：在区域R上求函数$f$的平均值： $$\overline{f}=\frac{1}{Area(R)}\int \! \! \!\int_RfdA$$ 也可以是加权平均，假设权重函数为密度函数$\delta$时，积分结果为$\frac{1}{M}\int \int_R\delta fdA$ 通过密度加权，可以求解物体的重心坐标：$(\overline{x},\overline{y})=(\frac{1}{M}\int !!!\int_R\delta xdA,\frac{1}{M}\int !!!\int_R\delta ydA)$

  3. 应用3：计算物体的转动惯量（物体绕轴旋转的困难程度）：

    已知$w$表示角速度，$r$表示旋转的半径，$v=r\cdot w$表示线速度 $E=\frac{1}{2}mv^2=\frac{1}{2}mr^2w^2$表示动能，则$mr^2$表示转动惯量$I_0$的积分计算方法如下： $$I=mr^2=\int \! \! \! \int_R r^2\cdot \delta dA$$

    • 物体旋转的困难程度取决于物体质量和物体距离转轴的长度
    • 以圆形飞盘为例，飞盘绕中心旋转时的旋转半径等于飞盘的半径；飞盘绕边缘旋转时的旋转半径等于飞盘的半径的两倍。所以飞盘绕边缘旋转的困难程度是绕中心旋转的四倍

3 参考

往年同期文章