1 金融领域常见指标
1.1 WoE(Weight of Evidence)
一般情况下,我们将正常客户标记为0,违约客户标记为1。那么WOE其实就是自变量取某个值时对违约比例的一种影响。其计算公式如下:
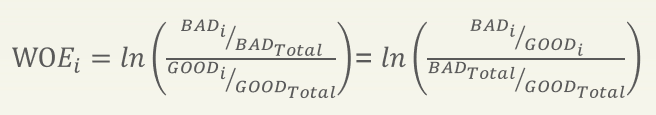
可以发现WoE公式反映的是自变量在第i个分组下坏客户对好客户的比例与总体坏客户对好客户占比之间的差异。在进行分析的时候,我们需要对各指标从小到大进行排序,计算出各分段对应的WoE。
1.2 CAP曲线
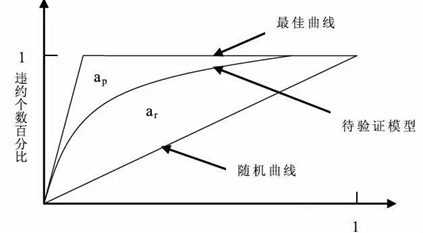
CAP曲线(Cumulative Accuracy Profile)是常用的衡量风险模型表现好坏与否的方法。我们可以直观地从CAP曲线中看出各个评分(或评级)结果下,累积违约客户比例和累积客户比例之间的关系。
CAP曲线的纵轴是违约总体中被观测到的比例 (percentage of defaulted companies being captured), 横轴是所有客户的比例 (percentage of total number of customer)。可以想象, 如果有一个模型可以将所有的违约客户筛选出来, 而且没有误判。 那模型的CAP Curve会是是一条斜率为PD (Probability of default) 并且停留在1的水平线。 而如果模型是一个随机模型, CAP曲线会是一条45度的直线。 如下图所示:
1.3 GINI/AR (Accuracy Ratio)
也称为基尼系数,是CAP曲线的具体量化描绘。公式如下:
$$AR=\frac{a_r}{(a_p+a_r)}$$
如果 AR值为1的话,模型预测能力更强。 如果AR值趋近于0的话, 则模型表现不佳。
1.4 K-S检验 (Kolmogorov-Smirnov Test )
#K-S #Kolmogorov-Smirnov #假设检验 #风险评估 #评分卡
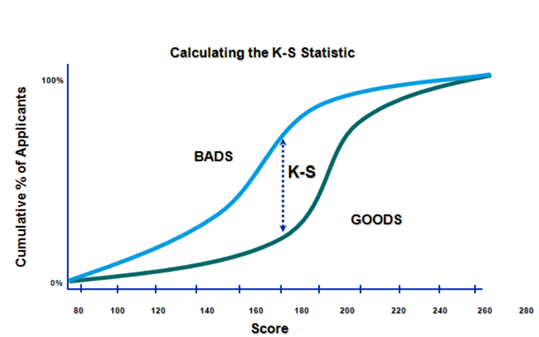
K-S是用来衡量评分卡预测能力的一个指标。我们使用K-S统计量对好坏客户区分能力进行量化,K-S统计量等于好客户和坏客户的累积概率差的最大值,即:
K−S=D=sup|F_n (x)−F_0 (x)|
2 模型常见评价指标
1 分类模型评价指标
2 回归模型评价指标
3 模型稳定性评价指标
3 多重共线性相关指标
3.1 统计检验类
F检验:拟合线性回归类模型,通过自变量系数是否为0线性关系
t检验:针对特定的自变量,判断其与因变量是否存在线性关系
假设检验还可以通过P值判断结论的显著性/可靠性,常用的判定阈值为0.05
除此之外,还可以进行数据相关性分析,比如计算相关系数,或进行差异性检验
3.2 拟合优度的衍生
线性模型的拟合优度$R^2$值为0时,也间接说明特征与预测变量间不存在线性关系。
而当自变量作为预测变量时,则可以评估特征间的多重共线性
基于拟合优度,衍生出了两个常见指标:容忍度(Tolerance)和方差膨胀系数(VIF)
容忍度(Tolerance): $$Tolerance=1-R^2$$
- 容忍度越小,多重共线性越严重
- 当容忍度小于0.1时,说明存在严重的多重共线性
方差膨胀系数(VIF): $$VIF_i=\frac{1}{1-R_i^2}$$
- 方差膨胀系数也被称为共线性指标
- 当方差膨胀系数为1时,意味着特征间不存在共线性
- 当方差膨胀系数大于10时,说明存在严重的多重共线性
3.3 特征值与解释度
从线性代数的角度考虑,存在多重共线性的特征构建出的矩阵,会表现出成分比重”头重脚轻“的情况,即前几个特征根和成分解释度偏高,最后几个特征根和成分解释度偏低
特征根(Eigenvalue):当存在特征根为0的情况,意味着存在严重的共线性
条件指数(Condition Index,CI):大于30时表明存在共线性问题 $$CI=\sqrt{\frac{最大的主成分}{当前主成分}}$$
变异构成(Variance Proportion):回归模型中各项(包括常数项)变异能被主成分解释的比例,比如某个主成分对多个自变量的贡献比例都大于0.5时,则表明这几个自变量之间存在共线性问题
4 信息准则类指标
对于统计模型,常需要评估模型复杂度和拟合效果,筛选出选择最合适的模型。信息准则类指标借助信息熵的概念实现了这种评估功能,最常见的包括AIC、BIC和HQ
符号说明
n:样本数 k:参数量 L:对数似然值
4.1 AIC
赤池信息准则(akaike information criterion): $$AIC=-2 ln(L) + 2 k$$
4.2 BIC
贝叶斯信息准则(bayesian information criterion): $$BIC=-2 ln(L) + ln(n)\ast k $$
4.3 HQ
汉南-奎因准则(hannan-quinn criterion): $$HQ=-2 ln(L) + ln(ln(n))\ast k$$