相关性度量
皮尔逊相关系数
皮尔逊积矩相关系数(Pearson product-moment correlation coefficient,简称PPMCC或PCCs)
- 最常见的相关系数,所以文章或教学中常见的"相关系数"指的就是皮尔逊相关系数
- 皮尔逊相关系数用于度量两组数据的变量X和Y之间的线性相关的程度
适用范围:
- 前提假设是两个变量是连续且服从正态分布
- 两组变量的样本量也应该尽可能保持一致
- 但是对于非独立非正态分布变量,研究皮尔逊积矩相关系数也是有意义的
皮尔逊相关系数的定义: $$\rho_{X,Y}=\frac{cov(X,Y)}{\sigma_X \sigma_Y}=\frac{E[(X-\mu_X)(Y-\mu_Y)]}{\sigma_X \sigma_Y}$$
- 其计算过程就是两个变量的协方差除以它们标准差的乘积
- 值域范围在-1~1之间,绝对值表示相关性强度,正负号表示相关性方向
斯皮尔曼相关系数
斯皮尔曼等级相关系数(等级相关系数,秩相关系数,Spearman's rank correlation coefficient)
- 当变量类型为次序/等级类型时,计算方式与皮尔逊相关系数一样
- 当变量类型为数值型时,先排序转化数值为次序,再计算
- 值域范围在-1~1之间,绝对值表示相关性强度,正负号表示相关性方向
适用范围:
- 比皮尔逊相关系数宽松很多
- 不需要考虑变量分布、样本量差异
- 不适用于非次序的类别型变量
肯德尔(kendall)相关系数
肯德尔等级相关系数(Kendall rank correlation coefficient)
- 一个用来测量两个随机变量(次序)相关性的统计值
- 值域范围在-1~1之间,绝对值表示相关性强度,正负号表示相关性方向
定义:样本对的一致性
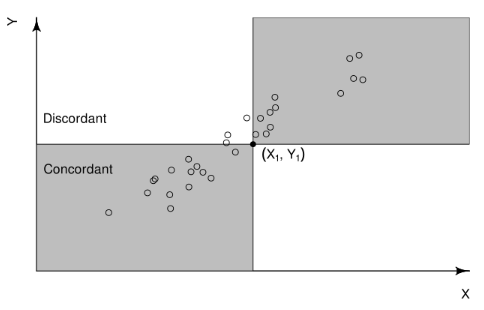
- 假设第$i$组样本为$(X_i,Y_i)$,第$j$组样本为$(X_j,Y_j)$,二者构成一个样本对
- 当$X_i<X_j$且$Y_i<Y_j$时,样本对被认为是一致的
- 当$X_i>X_j$且$Y_i>Y_j$时,样本对被认为是一致的
- 除了以上两种情况外,其他情况样本对被认为是不一致的
- 如上图所示,对于样本$(X_1,Y_1)$来说,灰色区域内的样本是一致的
肯德尔相关系数的定义: $$\tau=\frac{一致的样本对数-不一致的样本对数}{总样本对数}=1-\frac{2(不一致的样本对数)}{{n \choose 2}}$$
适用范围:与斯皮尔曼相关系数要求一样
余弦相似度
余弦相似度(Cosine Similarity)
- 计算两个向量的夹角余弦值来评估二者间的相似度
- 取值范围为
[-1,1],-1 表示完全不相似,1 表示完全相似
余弦相似度数的定义: $$\mathrm{Similarity(A,B)}\ =\frac{\mathrm{A\cdot B}}{\vert\vert\mathrm{A}\vert\vert\times\vert\vert\mathrm{B}\vert\vert}\ =\frac{\displaystyle\sum_{\mathrm{i=1}}^{\mathrm{n}}\left(\mathrm{A_{i}\times B_{i}}\right)}{\sqrt{\displaystyle\sum_{\mathrm{i=1}}^{\mathrm{n}}\mathrm{A_{i}^{2}\times}\sqrt{\displaystyle\sum_{\mathrm{i=1}}^{\mathrm{n}}\mathrm{B_{i}^{2}}}}}$$
余弦相似度的局限性:
- 用余弦相似度来比较句子间的语义相似性,可能会被词汇和语法相似性所干扰
- 谨慎使用余弦相似度作为训练目标,因为可能导致模型的过拟合或欠拟合
- 余弦相似度在处理高维向量、或包含空白或无意义的向量时更容易存在错误匹配
Jaccard 相似度
衡量两个集合之间相似性和差异性的重要指标
$$J(A,B)={\frac{|A\cap B|}{|A\cup B|}}$$
- 分子为集合 A 与集合 B 的交集的大小
- 分母为集合 A 与集合 B 的并集的大小
取值范围在 0~1,当值为 1 时表示两个集合完全相同
差异性检验
T检验
Y是连续型变量(正态齐次),X是二分类
F检验
Y是连续型变量(正态齐次),X是多分类
卡方检验
X和Y都是类别型变量
Tukey检验
Tukey检验,也称Tukey’s HSD (honestly significant difference)
- 一种适用于单步多重(分组数大于2)比较的统计检验方法
- 基于 studentized range 分布计算出q统计量,然后基于q进行两两间差异的假设检验
- 该方法适用于分组间等方差等数目的场景;分组内数目不同时要用 Tukey-Kranmer 方法
距离度量
Jaccard 距离
衡量两个集合之间的差异性 $$D(A,B)=1-J(A,B)$$
- 其中 $J(A,B)$ 表示 Jaccard 相似度
其他相关性分析
偏相关性
在给定 Z 的情况下,计算 X 和 Y 的相关性
偏相关性 (Partial correlation) 的计算方式 $${{\rho(X,Y|\mathbf{Z})=\rho(e_{X},e_{Y})=\frac{\mathrm{Cov}(e_{X},e_{Y})}{\sqrt{\mathrm{Var}(e_{X})]}{\sqrt{\mathrm{Var}(e_{Y})}}}}}$$
- $e_X$ 表示 X 对 Z 进行回归得到的残差:$e_{X}=X-(\beta_{X}^{T}\mathbf{Z}+\mathrm{intercept}_{X})$
- $e_Y$ 表示 Y 对 Z 进行回归得到的残差:$e_{Y}=Y-(\beta_{Y}^{T}\mathbf{Z}+\mathrm{intercept}_{Y})$
- $e_X$和 $e_Y$之间的皮尔逊相关系数,就是 X 和 Y 在控制 Z 后的偏相关性
偏相关性等于0,说明当且仅当X和Y在给定Z的条件下互相独立
Wilcoxon秩和检验
Wilcoxon秩和检验,有时也叫Mann-Whitney U检验
Y是连续型变量(非正态或非齐次),X是类别型
Box-Tidwell法
检验连续的自变量与因变量的logit转换值之间是否存在线性关系
HSIC
Hilbert-Schmidt Independence Criterion (HSIC)
利用核方法在高维空间中测量随机变量的相关性