主成分分析（Principal components analysis，PCA），一种常用的线性降维方法
算法步骤：
- 构建数据的协方差矩阵，并进行特征分解
- 特征向量描述的数据的主成分，特征值描述这一成分对应的权重
- 通过截断特征值较低的部分，保留数据集当中对方差贡献最大的特征
- 最终得到的降维特征无共线性（正交），但解释性差
图像理解：
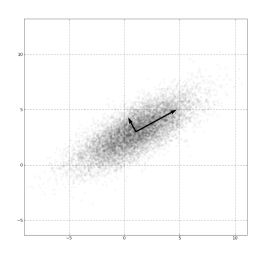（图源：维基百科-主成分分析）
- 上图为二元高斯分布（正态分布），均值为$(1,3)$，方差为$(0.878,0.478)$
- 黑色向量的方向描述的是协方差矩阵对应的特征向量
- 黑色向量的长度描述的是特征向量对应的特征值
PCA 的优缺点分析：
- 计算简单，易于实现；以方差衡量信息量，不受数据集以外的因素影响
- 各主成分之间正交，可消除原始数据成分间的相互影响的因素
- 降维后的主成分可解释性差，被丢弃的非主成分也可能包含重要信息
核主成分分析(Kernelized PCA, 简称KPCA）：使用核函数的主成分分析