核密度估计(kernel density estimation,简称KDE)是核平滑对概率密度估计的应用,即一种以核为权重估计随机变量概率密度函数的非参数方法。由Rosenblatt (1955)和Emanuel Parzen(1962)提出,又名Parzen窗(Parzen window)
核密度估计的实现:
- 假设$(x_1,x_2,...,x_n)$是来自同一个单变量未知分布中的独立样本
- 核密度估计可以根据这些样本推测出该分布的概率密度函数:
$$\hat{f}_h(x)=\frac{1}{n}\Sigma_{i=1}^nK_h(x-x_i)=\frac{1}{nh}\Sigma_{i=1}^nK\left(\frac{x-x_i}{h}\right)$$
- 上式中$K$表示核函数,常见的核函数为高斯核
- $h$是一个平滑函数,用于平衡估计结果的偏差和方差
除了估计密度函数外,核密度估计还常用于数据分布的可视化:
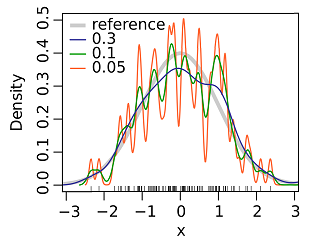
- 上图中,伴随着$h$变大,概率密度估计变得更加平滑