1 算法概况
局部线性嵌入(Locally Linear Embedding,以下简称LLE)是一种重要的降维方法。
和传统的PCA,LDA等关注样本方差的降维方法相比,LLE关注于降维时保持样本局部的线性特征,由于LLE在降维时保持了样本的局部特征,LLE广泛的用于图像图像识别,高维数据可视化等领域。
2 算法步骤
下图对LLE的原理进行了一个整体描述:
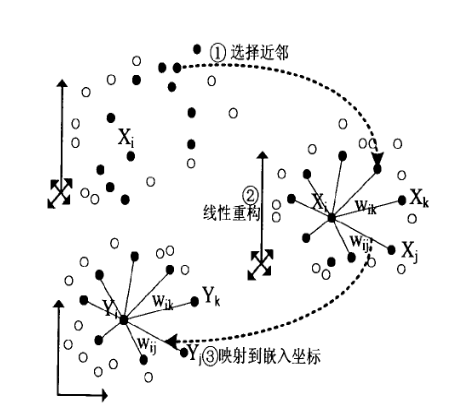
2.1 选择近邻:
- 求K近邻的过程,这个过程借助KNN算法找到最近邻的K个样本
- 简单来说 ,就是通过计算样本间的欧氏距离,找到最近的K个样本
2.2 线性重构:
- 假设样本$x_i$与K个近邻样本之间存在线性关系/回归系数$w_{ij}$
- 使用均方差作为回归问题的损失函数:
$$J=\Sigma_i||x_i-\Sigma_jw_{ij}x_j||^2_2$$
- 增加权重的归一化约束$\Sigma_i w_ij=W^T_i1_k=1$,$w_{ij}$的求解转化为带约束的最优化问题
- 使用拉格朗日乘子法求解计算$w_{ij}$:$L=J+\lambda(W^T_i1_k-1)$
- 得到权重系数向量的通用解析式(令偏导=0并化简后可得):
$$W_i=\frac{Z_i^{-1}1_k}{1^T_kZ_i^{-1}1_kk}$$
- 其中$Z_i=(x_i-x_j)(x_i-x_j)^T$表示局部协方差矩阵
$||x_i||2^2$表示向量$x_i$的欧几里得范数$\sqrt{x\{i1}^2+...+x_{in}^2}$的平方,即$x_{i1}^2+...+x_{in}^2$
2.3 映射到低维坐标:
核心思想:通过维持回归系数不变,在低维里重构样本数据
- 假设样本$x_i$对应的低维投影为$y_i$,此时低维重构对应的损失函数:
$$J=\Sigma_i||y_i-\Sigma_jw_{ij}y_j||^2_2=\Sigma_i||YI_i-YW_i||=tr(Y(I-W)(I-W)^TY^T)$$
- 假设$M=(I-W)(I-W)^T$,则$J=tr(YMY^T)$,其中$tr$表示迹函数
- 增加对低维投影的标准化约束(均值0,方差1):$\Sigma_{i=1}^my_i=0,\frac{1}{m}\Sigma_{i=1}^my_iy_i^T=I,$
- 继续使用拉格朗日乘子法求解:$L=tr(YMY^T+\lambda(YY^T-mI))$
- 得到结果$MY^T=-\frac{1}{2}\lambda Y^T$,所以$Y^T$是矩阵$M$的特征向量矩阵
- 当投影的维度$=d$时,矩阵$Y=(y_1,...,y_n)^T$是$M$最小的$d$个特征值对应的特征向量矩阵
矩阵$M$的0特征值对应的特征向量全为1,不能反应数据特征,所以一般选择$M$的第2个到第d+1个特征值对应的特征向量矩阵,作为最终的结果$Y$
之所以选择偏小的特征值对应的特征向量矩阵,是因为最优化的目标函数与保留的特征值存在正相关性,所以保留的特征值越小,对应的损失$J$也就越小
3 算法分析
总结:LLE是广泛使用的图形图像降维方法,它实现简单,但是对数据的流形分布特征有严格的要求。比如不能是闭合流形,不能是稀疏的数据集,不能是分布不均匀的数据集等等,这限制了它的应用。下面总结下LLE算法的优缺点。
优点
- 可以学习任意维的局部线性的低维流形
- 算法归结为稀疏矩阵特征分解,计算复杂度相对较小,实现容易
缺点
- 算法所学习的流形只能是不闭合的,且样本集是稠密均匀的
- 算法对最近邻样本数的选择敏感,不同的最近邻数对最后的降维结果有很大影响
算法变种:
- Modified Locally Linear Embedding(MLLE):从降维过程中保持局部的线性关系,改为保持局部的海森矩阵的二次型的关系
- Hessian Based LLE(HLLE):改进K近邻的选择,使得近邻样本尽量在样本的不同方位
参考文献: 刘建平-局部线性嵌入(LLE)原理总结