1 基本概念
模拟退火算法(Simulated Annealing,SA)的思想最早是由Metropolis等提出的。物理中固体物质的退火过程与一般的组合优化问题之间的相似性,SA是一种由物理退火过程启发的通用优化算法
模拟退火法的物理过程:
- 加温过程:其目的是增强粒子的热运动,使其偏离平衡位置。当温度足够高时,固体将熔为液体,从而消除系统原先存在的非均匀状态
- 等温过程:对于与周围环境交换热量而温度不变的封闭系统,系统状态的自发变化总是朝自由能减少的方向进行的,当自由能达到最小时,系统达到平衡状态
- 冷却过程:使粒子热运动减弱,系统能量下降,得到晶体结构。
2 算法过程
SA算法解决优化问题的基本思路:
- 加温过程对应算法的初始温度设定(一开始要足够高温),等温过程对应算法的Metropolis抽样过程,冷却过程对应控制参数的下降。
- 能量的变化就是目标函数,最优解就是对应着能量发最低态
- Metropolis准则以一定的概率接受恶化解,是算法收敛于全局最优解的关键所在
SA算法核心过程:
- 初始化:取初始温度$T_0$足够大,令$T= T_0$,任取初始解$S_1$
- 假设已经迭代到了第$k$个解$S_k$,对当前解$S_k$随机扰动产生一个新解$S_{k+1}$
- 计算$S_{k+1}$的增量$\Delta f= f(S_{k+1})-f(S_k)$,其中$f$为代价函数
- 若$\Delta f<0$则接受$S_{k+1}$作为新的当前解;否则计算$S_{k+1}$的接受概率$e^{-\Delta f/T}$, 即随机产生$(0,1)$区间上均匀分布的随机数$r$,若$e^{-\Delta f/T}>r$,接受$S_{k+1}$作为新的当前解,否则保留当前解$S_k$
- 如果满足终止条件,则输出当前解为最优解,结束程序;否则对温度$T$衰减后返回第2步
在经典模拟退火算法中,其温度的衰减满足以下公式: $$T(t)=\frac{T_0}{log(1+t)}$$
终止条件通常为最大连续无效(无效=新解没有被接受)迭代次数或者是设定结束温度
3 算法分析
SA算法分析:
- 初始温度越高,算法耗时越长,最终获得高质量解的可能性也越高
- 模拟退火算法不属于群优化算法,不需要初始化种群操作
- 收敛速度较慢;温度管理、退火速度等对寻优结果均有影响
4 代码实现
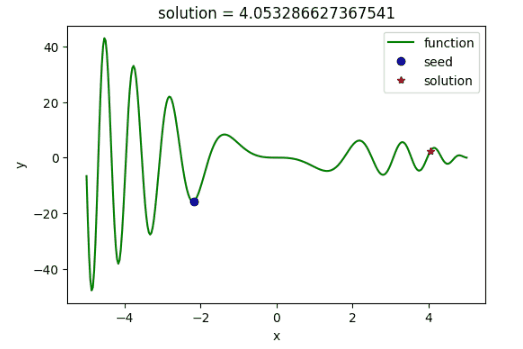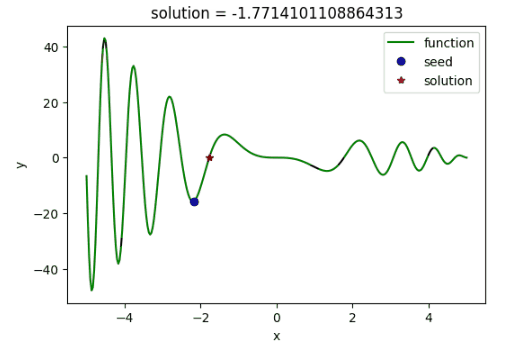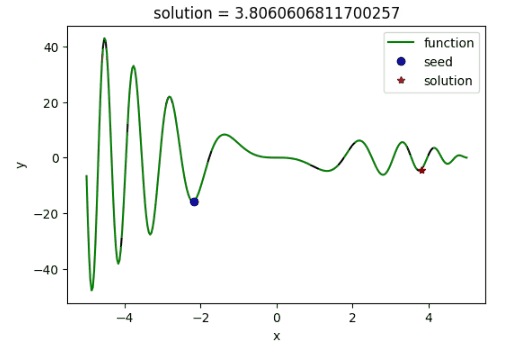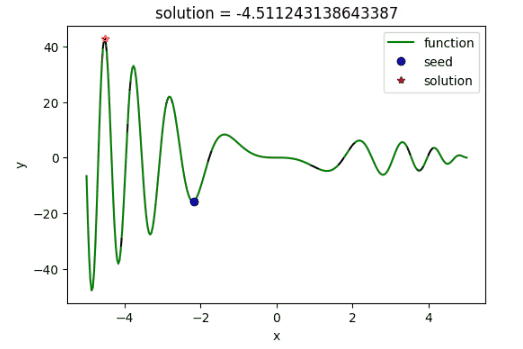
使用模拟退火算法寻找函数$f(x)=(x^2-5x)sin(x^2)$的最大值
import numpy as np
import matplotlib.pyplot as plt
import random
# 参考链接:https://www.cnblogs.com/xxhbdk/p/9192750.html
class SA(object):
def __init__(self, interval, tab='min', T_max=10000, T_min=1, iterMax=1000, rate=0.95):
self.interval = interval # 给定状态空间 - 即待求解空间
self.T_max = T_max # 初始退火温度 - 温度上限
self.T_min = T_min # 截止退火温度 - 温度下限
self.iterMax = iterMax # 定温内部迭代次数
self.rate = rate # 退火降温速度
self.x_seed = random.uniform(interval[0], interval[1]) # 解空间内的种子
self.tab = tab.strip() # 求解最大值还是最小值的标签: 'min' - 最小值;'max' - 最大值
self.solve() # 完成主体的求解过程
def solve(self):
temp = 'deal_' + self.tab # 采用反射方法提取对应的函数
if hasattr(self, temp):
deal = getattr(self, temp)
else:
exit('>>>tab标签传参有误:"min"|"max"<<<')
x1 = self.x_seed
T = self.T_max
num = 1
while T >= self.T_min:
for i in range(self.iterMax):
f1 = self.func(x1)
delta_x = random.random() * 2 - 1 # [-1,1)之间的随机值
if x1 + delta_x >= self.interval[0] and x1 + delta_x <= self.interval[1]: # 将随机解束缚在给定状态空间内
x2 = x1 + delta_x
else:
x2 = x1 - delta_x
f2 = self.func(x2)
delta_f = f2 - f1
x1 = deal(x1, x2, delta_f, T)
T *= self.rate
num +=1
if num %10 == 0:
self.display(x1) # 数据可视化展示
self.x_solu = x1 # 提取最终退火解
self.display(self.x_solu)
def func(self, x): # 状态产生函数 - 即待求解函数
value = np.sin(x**2) * (x**2 - 5*x)
return value
def p_min(self, delta, T): # 计算最小值时,容忍解的状态迁移概率
probability = np.exp(-delta/T)
return probability
def p_max(self, delta, T):
probability = np.exp(delta/T) # 计算最大值时,容忍解的状态迁移概率
return probability
def deal_min(self, x1, x2, delta, T):
if delta < 0: # 更优解
return x2
else: # 容忍解
P = self.p_min(delta, T)
if P > random.random(): return x2
else: return x1
def deal_max(self, x1, x2, delta, T):
if delta > 0: # 更优解
return x2
else: # 容忍解
P = self.p_max(delta, T)
if P > random.random(): return x2
else: return x1
def display(self, x1):
print('seed: {}\nsolution: {}'.format(self.x_seed, x1))
plt.figure(figsize=(6, 4))
x = np.linspace(self.interval[0], self.interval[1], 300)
y = self.func(x)
plt.plot(x, y, 'g-', label='function')
plt.plot(self.x_seed, self.func(self.x_seed), 'bo', label='seed')
plt.plot(x1, self.func(x1), 'r*', label='solution')
plt.title('solution = {}'.format(x1))
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
# plt.savefig('SA.png', dpi=500)
display.clear_output(wait=True)
plt.pause(0.001)
if __name__ == '__main__':
SA([-5, 5], 'max')