LDA 算法是一种监督学习的降维技术
- LDA 算法将高维空间中的d维数据通过投影转化成1维数据进行处理
- 对于训练数据,LDA 算法会让同类数据的投影点尽可能接近,异类数据尽可能远离
- 对于新数据分类,LDA 算法会先进行数据投影,再根据投影点位置来确定样本的类别
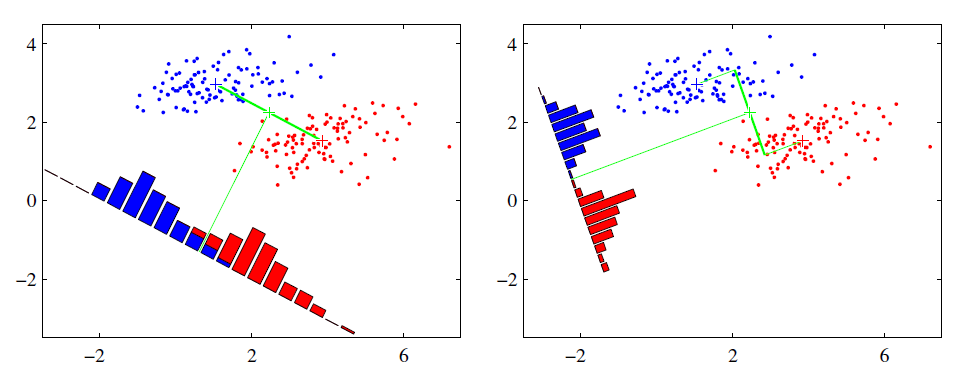
- 左图思路:让不同类别的平均点距离最远的投影方式
- 右图思路:让同类别的数据距离最近的投影方式
LDA算法降维流程如下:
输入:数据集 $D = { (x_1,y_1),(x_2,y_2), ... ,(x_m,y_m) }$,其中样本 $x_i$ 是n维向量,$y_i \in {C_1, C_2, ..., C_k}$,降维后的目标维度 $d$ 。
输出:降维后的数据集 $\overline{D}$ 。
步骤:
- 计算两个类别的中心点 $u_0$, $u_1$
- 计算类内散度矩阵 $S_w= \sum_{\boldsymbol x\epsilon X_0}(\boldsymbol x-u_0)(\boldsymbol x-u_0)^T + \sum_{\boldsymbol x\epsilon X_1}(\boldsymbol x-u_1)(\boldsymbol x-u_1)^T$
- 计算类间散度矩阵 $S_b = (u_0 - u_1)(u_0 - u_1)^T$
- 构建矩阵 $S^{-1}_wS_b$ 并计算$S^{-1}_wS_b$ 的最大的$d$个特征值
- 计算$d$个特征值对应的$d$个特征向量,记投影矩阵为$W$
- 转化样本集的每个样本,得到新样本 $P_i = W^Tx_i$ 。
- 输出新样本集 $\overline{D} = { (p_1,y_1),(p_2,y_2),...,(p_m,y_m) }$
LDA 的优缺点分析:
- 以标签、类别衡量差异性的有监督降维方式,可以使用类别的先验知识
- 相对于 PCA 的模糊性,LDA 目的更明确,更能反映样本间的差异
- LDA不适合对非高斯分布样本进行降维,降维最多降到分类数k-1维
- LDA 在样本分类依赖方差而不是均值时,降维效果不好且可能过拟合