图论起源：柯尼斯堡七桥问题
1 基础概念
图 (graph) 常用$G=(V,E)$表示，其中$V$表示顶点/节点的集合，$E$表示边的集合
相邻的 (adjacent)/关联的 (incident)
- 边两端的顶点和边的关系是关联的或相邻的
- 通过边相连接的两个顶点之间的关系是相邻的
顶点的度 (degree)：与该顶点关联的边的条数。
- 对于有向图来说，以一个顶点为起点的边的条数称作该顶点的 出度 (out-degree)；以一个顶点为终点的边的条数称作该顶点的 入度 (in-degree)；
- 对于有权图来说，一个顶点的度=该顶点关联的边的权重和
途径 (walk)：连接一连串顶点的边的序列，可以为有限或无限长度
- 迹 Trail：不包含重复边的walk
- 路径 Path：不包含重复顶点的Trail
- 回路 Cycles： 封闭的Trail，即只有起终点指向同一个的顶点
- 环/圈 Circuit： 封闭的Trail,，允许有重复的顶点
子图（subgraph）：当图$H=(V',E')$满足$V'\subseteq V$且$E'\subseteq E$时，$H$是$G$的子图
简单图 (simple graph)：一个没有自环和重边的图
- 自环 (loop)是指边的两端指向同一个顶点的情况
- 重边 (multiple edge)是指两个边具备相同的起点和重点
度矩阵（Degree matrix，简称$D$）、邻接矩阵（Adjacency matrix，简称$A$）、拉普拉斯矩阵（Laplacian matrix，简称$L$）三者关系如下图所示：
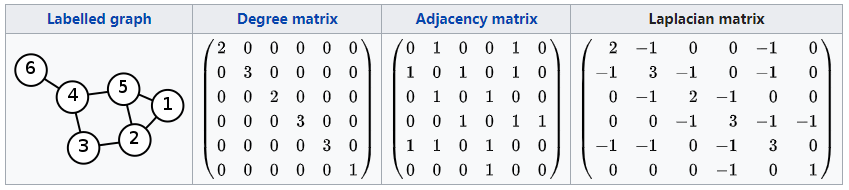图源：wikipedia-Laplacian matrix
2 常见类型
2.1 图的常见类型
根据$V$或$E$是否为无限集合，可以将$G$划分为无限图和有限图
根据边是否存在权重，可以将$G$划分为有权图和无权图
根据边是否具备方向，可以将$G$划分为有向图(directed graph) 和无向图 (undirected graph)；而既包含有向边，也包含无向边的图也被称为混合图 (mixed graph)
根据连通性划分图：
- 连通图 (connected graph)：无向图中任意两个顶点是连通的
- 强连通图：有向图中任意两个顶点是连通的（互相可达）
- 弱连通图：有向图中的边替换为无向边后，任意两个顶点是连通的
完全图：任意两顶点之间都有边相连的无向图
有向无环图（Directed Acyclic Graph，简称DAG）
同质图（Homogeneous Graph）：只有一种类型的节点和一种类型的边的图 异质图（Heterogeneous Graph）：存在多种类型的节点和多种类型的边的图
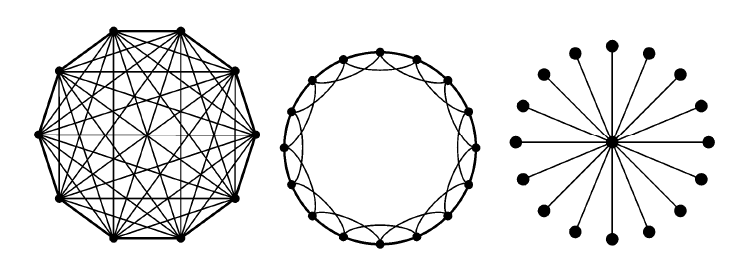
根据拓扑结构，图可以分为全连接网络、环形网络、星形网络：
2.2 顶点的常见分类
根据度的不同，顶点的分类如下：
- 孤立点(isolated vertex)：度为0的顶点
- 叶节点 (leaf vertex)/悬挂点 (pendant vertex)：度为1的顶点
- 偶点 (even vertex)：度为偶数值的顶点
- 奇点 (odd vertex)：度为奇数值的顶点
- 支配点 (universal vertex)：度为$|V|-1$的顶点
一个图中奇点的个数是偶数
2.3 图的同构与子图同构
图同构（Graph Isomorphism）问题：检查两个图是否是相同的
两个图 $G$ 和 $H$，如果存在一个双射 $f : V (G) \to V (H)$，且满足 $(u, v)\in E (G)$，当且仅当 $(f (u), f (v))\in E (H)$，则我们称 $f$ 为 $G$ 到 $H$ 的一个同构 (isomorphism)，且图 $G$ 与图 $H$ 是同构的 (isomorphic)，记作 $G \cong H$。
双射：两个集合间的元素是一一对应的，并且不同的元素的映射结果不同
上图左侧中，可以通过定义出一个双射同构 $f$（黄转红，红转绿，蓝转黄，绿转蓝），因此两个图是同构的；上图右侧中，无法定义出一个双射同构 $f$，因此是非同构的
从定义可知，若 $G \cong H$，必须满足：
- $|V (G)|=|V (H)|,|E (G)|=|E (H)|$
- $G$ 和 $H$ 结点度的非增序列相同
- $G$ 和 $H$ 存在同构的导出子图
如果 $G2$ 的某个子图同构于 $G1$，则称 $G2$ 是 $G1$ 的子图同构（subgraph-isomorphic）
目前未找到图同构问题的多项式算法，也尚不清楚该问题是否为 NP-Hard问题；不过可以确定子图同构问题是一个 NP-Hard 问题
3 图论进阶
3.1 理解拉普拉斯矩阵
- 由于$D$和$A$都是对称矩阵，因此$L=D-A$也是对称矩阵
对称矩阵的特征值为实数，具有完全正交的特征向量（可作为正交基）
- 拉普拉斯矩阵是一种对于图的矩阵表示，比如上图中第一行（因为是对称矩阵，所以也可以看第一列）描述的是顶点1的连接情况，顶点1的度为2，所以矩阵元素$l_{11}=2$，顶点1连接到顶点2和顶点5，所以矩阵元素$l_{12}=l_{15}=-1$
函数$f$的拉普拉斯算子$\nabla^2f$定义为函数 $f$ 梯度的散度，描述的是梯度场的发散性。而梯度可看作偏导构成的向量，能够描述自变量波动对因变量的影响。
同理，拉普拉斯矩阵$L$也被称为离散拉普拉斯算子，描述了图的发散性，刻画了图信号的整体平滑度；也可以评估某一个节点的改变，对于周围邻接节点的影响
对于任意的向量$f\in R^{n\times 1}$，$f^TLf=\Sigma_id_if_i^2-\Sigma_{ij}a_{ij}f_if_j=\frac{1}{2}\Sigma_{ij}a_{ij}(f_i-f_j)^2$，所以拉普拉斯矩阵作为一种算子时，能够基于欧氏距离的测度描述多个节点之间的离散程度（距离和），同时根据最右推导结果，易知$L$是半正定矩阵，特征值最小为0
拉普拉斯矩阵的0特征值数量等于图连通区域的数量；当整个图都是连通的时候，只会有一个0特征值；并且每个0特征值对应的特征向量对应着图连通区域的顶点集合
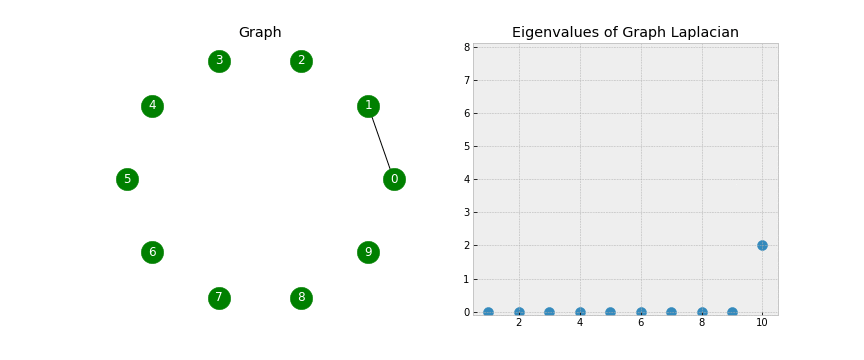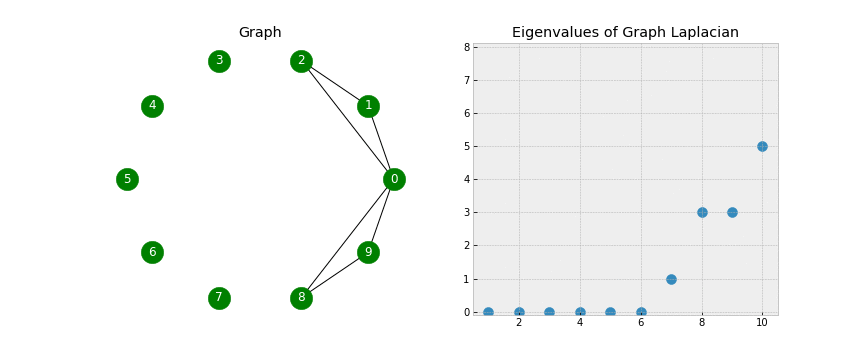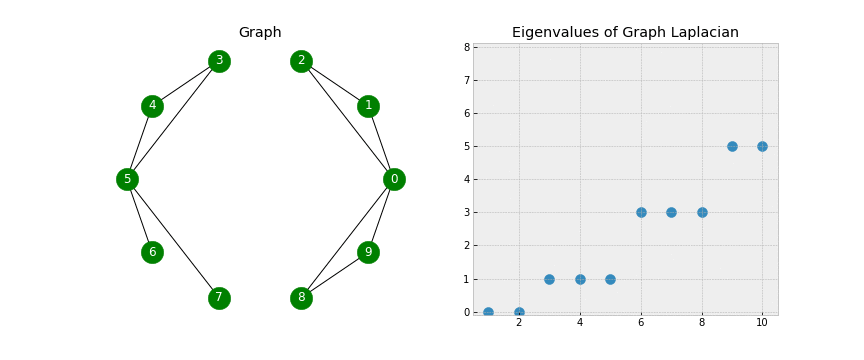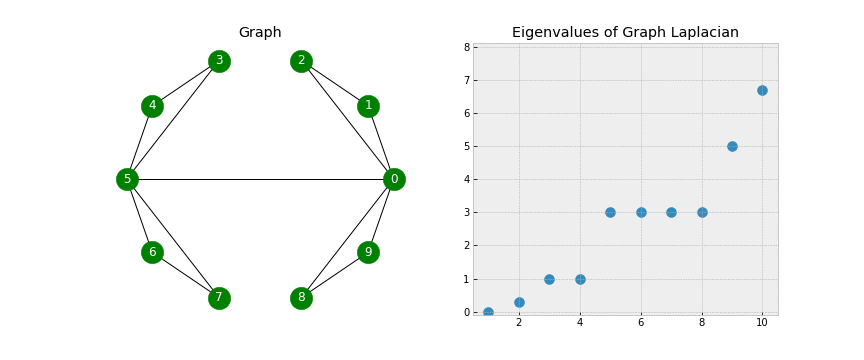
拉普拉斯矩阵可以进行谱分解（Spectral decomposition，也就是特征分解Eigendecomposition）：$L=U\Lambda U$，其中$\Lambda$由特征值$\lambda$组成，$U$由特征向量$u$组成
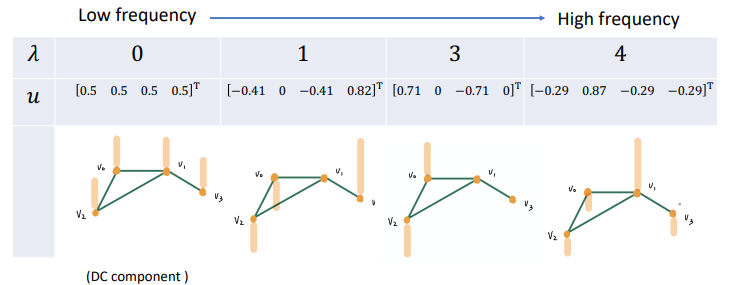
随着特征值的增大，特征向量中相邻节点间的差异逐渐变得明显。所以从频域的角度来看，特征值描述了特征向量的频率，特征值越高，对应的信号变化越剧烈；这也是图的傅里叶变换使用拉普拉斯矩阵的原因
拉普拉斯矩阵的归一化：
- 对称型（symmetric）：$L_{sym}=D^{-1/2}LD^{-1/2}=I-D^{-1/2}LW^{-1/2}$
- 随机游走型（random walk）：$L_{rw}=D^{-1}L=I-D^{-1}W$
- 归一化的拉普拉斯矩阵的特征值区间为
[0, 2]
拉普拉斯矩阵的应用
- 一种基于图的降维算法：拉普拉斯特征映射 LE
- 一种基于图的聚类算法：谱聚类
3.2 欧拉路问题
欧拉路（Eulerian path）：存在这样一种图，可以从其中一点出发不重复地走完其所有的边
欧拉回路（Euler circuit）：欧拉路的起点与终点相同
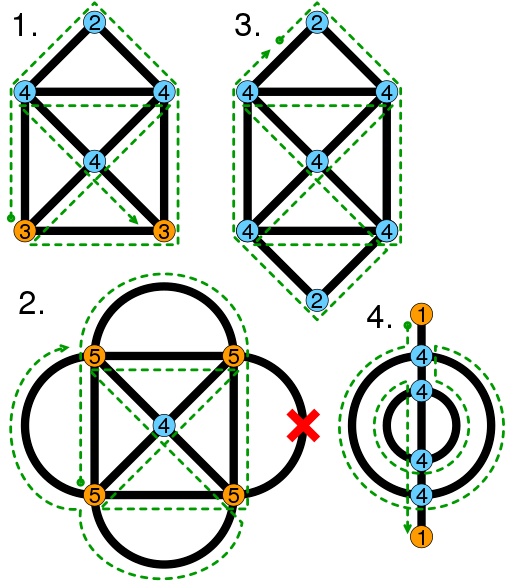
欧拉路存在的充要条件：
- 图是连通的，若不连通不可能一次性遍历所有边。
- 对于无向图：有且仅有两个点，与其相连的边数为奇数，其他点相连边数皆为偶数；或所有点皆为偶数边点。对于两个奇数点，一个为起点，一个为终点。起点需要出去，终点需要进入，故其必然与奇数个边相连。
- 如果存在这样一个欧拉路，其所有的点相连边数都为偶数，那说明它是欧拉回路。因为此时它的起点即是终点，出去后还会回来，刚好形成偶数边。
- 对于有向图：除去起点和终点，所有点的出度与入度相等。起点出度比入度大1，终点入度比出度大1。若起点终点出入度也相同，则为欧拉回路。
欧拉路问题也常被称为“一笔画问题”
3.3 超图 Hypergraph
超图的边（超边，hyperedge）可以和任意个数的顶点连接
超图示例（7个顶点4条边的超图）：
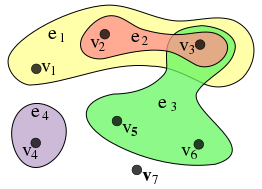
k-均匀超图（k-uniform hypergraph），指超图的每个边连接的顶点个数都是相同的，即为个数 k；所以普通图其实是超图的一个子集，即2-均匀超图
定义一个关联矩阵 $H$ 来描述超图，超图对应的顶点集为 $V$，超边集为 $E$ $$ \left . h ( v , e ) = \left { \begin{array} { c c c } 1 , \mathrm{ i f ~ } v \in e \\ 0 , \mathrm{ i f ~ } v \notin e \end{array} \right . \right . $$ 已知普通图的拉普拉斯的对称型归一化为：$L_{sym} = I-D^{-1/2}LW^{-1/2}$
拓展到超图上，则有：$L = I - D_{v}^{-1/2}HWD_{e}^{-1}H^TD_v^{-1/2}$
- 其中 $D_v$ 是顶点的度矩阵，$D_e$ 是超边的度矩阵