1 傅里叶变换
1.1 基本定义
传统傅里叶变换的定义为(积分形式):$F(\omega)=\mathcal{F}{f(t)}=\int f(t)e^{-i\omega t}dt$
传统逆傅里叶变换的定义为(积分形式):$f(t)=\mathcal{F}^{-1}{F(\omega)}=\frac{1}{2\pi}\int F(\omega)e^{i\omega t}d\omega$
卷积定理:函数卷积的傅里叶变换是函数傅立叶变换的乘积 $$f\ast g=\mathcal{F}^{-1}{\mathcal{F}{f}\cdot \mathcal{F}{g}}$$
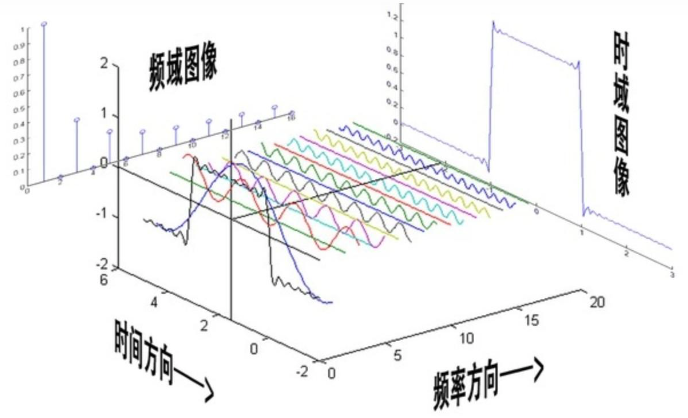
1.2 理解傅里叶变换
傅里叶变换的核心是从时域到频域的变换,而这种变换是通过一组特殊的正交基来实现的
2 快速傅里叶变换
https://oi-wiki.org/math/poly/fft/
#待补充
3 图的傅里叶变换
前置知识:图论基础
图域卷积时,使用拉普拉斯矩阵$L$的特征向量$U=[u_1,...,u_n]$作为傅里叶变换的基 $$L=U\Lambda U^T=U \begin{bmatrix} \Lambda_{1} \\
& \ddots \\ & & \Lambda_{n} \\ \end{bmatrix}U^T$$
传统傅里叶变换的本质是将信号分解到一组正交基上,而拉普拉斯矩阵作为一种半正定对称矩阵,总可以实现特征分解(谱分解),对应的特征向量也天然地满足正交基假设,适合用来作为图的傅里叶变换基
类比传统傅里叶变换的定义,图的傅立叶变换可定义如下(求和形式):$$F(\Lambda_i)=\mathcal{F}{f(j)}=\Sigma_{j=1}^N f(j)u_{ij}$$ 图的逆傅立叶变换可定义如下(求和形式): $$f(j)=\mathcal{F}^{-1}{F(\Lambda_i)}=\Sigma_{i=1}^N F(\Lambda_i)u_{ij}$$
因此,图的傅立叶变换$\mathcal{GF}$及其逆变换$\mathcal{IGF}$的矩阵形式可表示如下: $$\mathcal{GF}{f(x)}=U^T f(x)\ \ ,\ \mathcal{GF}^{-1}{f(x)}=Uf(x)$$ 传统傅里叶变换 VS 图的傅里叶变换:
- 传统傅里叶变换使用$e^{-i\omega t}$作为傅里叶变换基,使用$e^{i\omega t}$作为逆傅里叶变换基
- 图的傅里叶变换使用$U^T$作为傅里叶变换基,使用$U$作为图的逆傅里叶变换基
- 传统傅里叶变换的变换基有无限个,而图的傅里叶变换是有限个(特征向量数)
- 拉普拉斯矩阵的特征值$\Lambda$也具备频率的含义,和傅里叶变换的频率$\omega$存在等价关系
给定函数$f$和函数$h$,二者在图域的卷积运算可转化为傅里叶域的相乘: $$f\ast h=U(U^Tf \odot U^Th)$$
- 其中$\odot$表示哈达马积(Hadamard product),即同阶矩阵对应位置元素相乘
上式的一个等价写法: $$f \ast h = U \begin{bmatrix} \hat{h}(\lambda_1) \\
& \ddots \\ & & \hat{h}(\lambda_n) \\ \end{bmatrix}U^Tf$$
- 其中$\hat{h}$表示函数$h$经过傅里叶变换后的傅里叶域形式
- 这一等价写法的具体推导证明过程可参阅GCN中的等式证明