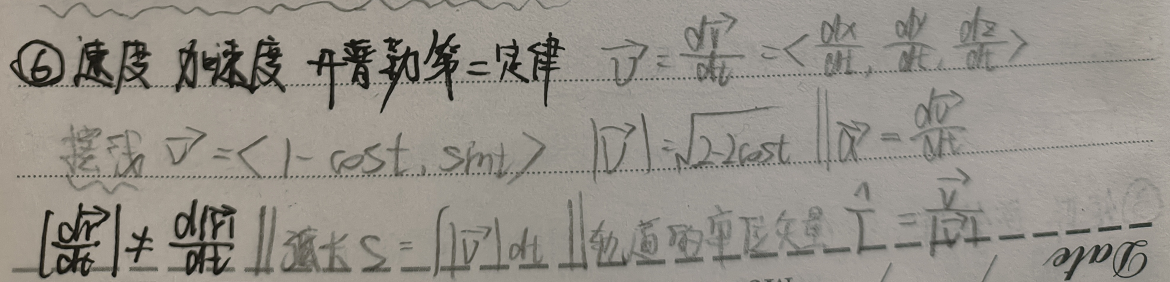1 速度与加速度
由上一节5.直线和曲线的参数方程可知,向量$\vec{r}(t)=x(t)\hat{i}+y(t)\hat{j}+z(t)\hat{k}$
且摆线轨迹$\vec{r}(\theta)=<a\theta-asin(\theta),a-acos(\theta)>$
定义速度: $$\vec{v}=\frac{d\vec{r}}{dt}=<\frac{dx}{dt},\frac{dy}{dt},\frac{dz}{dt}>$$
设半径$a=1$,则轨迹向量对应的速度$\vec{v}=<1-cost, sint>$,长度$|\vec{v}|=\sqrt{2-2cost}$
同理,可得加速度的定义: $$\vec{a}=\frac{d\vec{v}}{dt}$$ 则轨迹向量对应的加速度$\vec{a}=<sint, cost>$
注意(左侧结果的实际含义为速率,右侧是对模长函数的求导,无实际意义): $$|\frac{d\vec{r}}{dt}|\neq\frac{d\vec{|r|}}{dt}$$
2 弧长与单位矢量
用$S$表示沿轨迹运动的路程(弧长),则速率$|\vec{v}|=\frac{dS}{dt}$
弧长的常见计算方法为积分法:$S=\int{|\vec{v}|}dt$
定义轨道的单位矢量: $$\hat{T}=\frac{\vec{v}}{|\vec{v}|}$$ 由以下方程等式: $$\vec{v}=\frac{d\vec{r}}{dt}=\frac{d\vec{r}}{ds}\frac{ds}{dt}=\frac{d\vec{r}}{ds}\cdot |\vec{v}|$$ 可知: $$\hat{T}=\frac{\vec{v}}{|\vec{v}|}=\frac{d\vec{r}}{ds}$$
3 开普勒第二定律
太阳和行星在同一个面中,且二者连线在相同时间内扫过的面积相同
设行星在时间$\Delta{t}$内的轨迹向量为$\Delta{\vec{s}}$,速度向量为$\vec{v}$,则$\Delta{\vec{s}}\approx\vec{v}\cdot \Delta{t}$
设太阳和行星相连所构成的向量为$\vec{r}$,则此时间段内扫过的面积为: $$Area\approx \frac{1}{2}|\vec{r}\times \Delta{\vec{s}}|=\frac{1}{2}|\vec{r}\times \vec{v}|\Delta{t}$$ 由开普勒第二定律可知,单位时间内扫过的面积为常数,即: $$|\vec{r}\times \vec{v}|=常数$$ $$\frac{d}{dt}(\vec{r}\times \vec{v})=0$$ 化简得: $$\frac{d}{dt}(\vec{a}\times \vec{v})=\frac{d\vec{r}}{dt}\times \vec{v}+\vec{r}\frac{d\vec{v}}{dt}=\vec{v}\times\vec{v}+\vec{r}\times\vec{a}=0$$ 由叉积定义可知$\vec{v}\times\vec{v}=0$,所以$\vec{r}\times\vec{a}=0$,即两个向量是平行的
已知加速度$\vec{a}$的方向与力的方向是一致的,所以太阳和行星之间存在一种作用力,使得开普勒第二定律成立,也就是万有引力~
4 参考