1 直线的参数方程
假设$t=0$和$t=1$分别对应直线上的点$Q_0=(-1,2,2)$和$Q_1=(1,3,-1)$
易得$\overrightarrow{Q_0 Q(t)}=t\overrightarrow{Q_0 Q_1}$并且$Q(t)=(x(t),y(t),z(t))$,所以$Q(t)=Q_0+t\overrightarrow{Q_0 Q_1}$。即:
$$\begin{equation} \left\{ \begin{gathered} x(t) = -1+2t \ \\ y(t) = 2+t \ \\ z(t) = 2-3t \end{gathered} \right. \end{equation} $$ 而这就是过点$Q_0$和点$Q_1$的直线的参数方程
2 参数方程的应用
计算上一节直线与平面$x+2y+4z=7$的交点
思考:将$Q_0$带入平面方程左侧可得结果为$11>7$,将$Q_1$带入平面方程左侧可得结果为$3<7$,所以点$Q_0$位于平面上方,点$Q_1$位于平面下方。直线与平面必然存在交点。
求解:将直线的参数方程带入平面方程,可得$x(t)+2y(t)+4z(t)=7$,即可解得$t=\frac{1}{2}$,所以交点坐标为$Q(\frac{1}{2})=(0,\frac{5}{2},\frac{1}{2})$
3 摆线的参数方程
摆线(Cycloid)产生于半径为$a$的圆,是圆上的某一点$M$随圆滚动所产生的轨迹:
 (图源:维基百科-摆线)
(图源:维基百科-摆线)
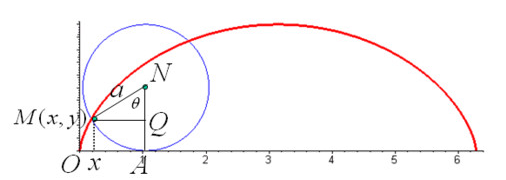
以角度$\theta$为自变量,则点$M$的坐标为$M=(x(\theta),y(\theta))$,设原点为$O$,可得: $$\overrightarrow{OM}=\overrightarrow{OA}+\overrightarrow{AN}+\overrightarrow{NM}$$
 (图源:中科大课件)
(图源:中科大课件)
此处分析只考虑第一个周期,因为后续的轨迹相当于第一次轨迹的平移
- 其中$\overrightarrow{OA}$的长度等于曲线$PA$的长度,所以$\overrightarrow{OA}=<a\theta,0>$
- 易得,$\overrightarrow{AN}=<0,a>$,而$\overrightarrow{NM}=<-asin(\theta),-acos(\theta)>$
- 综上所得,所以$\overrightarrow{OM}=<a\theta-asin(\theta),a-acos(\theta)>$
过渡点的分析:过渡点指连续两次滚动周期之间的衔接点,此时随着$\theta$趋近于$0$,$(1-cos(\theta))/(\theta-sin(\theta))$趋近于正无穷,即过渡点的切线垂直于$x$轴
4 参考
