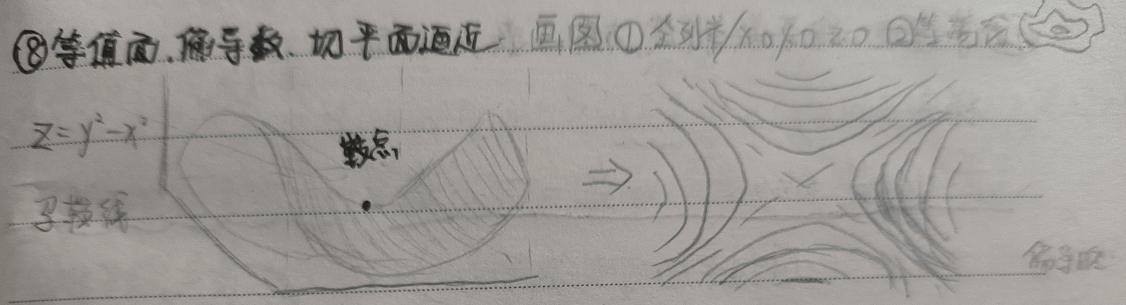
1 多元函数的绘图
随着自变量的增多,单变量函数开始向多元函数演变。而由于收到维度的限制,函数的可视化一般局限于二元函数图像与三元函数的等值面图像。其中等值面通过固定多元函数的因变量为常数而得到,以函数$z=x^2+y^2$为例,其绘图过程如下:
- 绘制坐标轴,一般采用右手坐标系
- 特殊情况的全列举,比如选定$x=0$,绘制函数在$yz$平面上的图像;选定$y=0$,绘制函数在$xz$平面上的图像;选定$z=0$,绘制函数在$xy$平面上的图像
- 选定$z=a$,其中$a$为任意常数,绘制多个等值面图像
密集的等值面图像可以直接构建多元函数的图像,而稀疏的等值面图像则可以同时投影到一个平面内,构建出等高线图像:
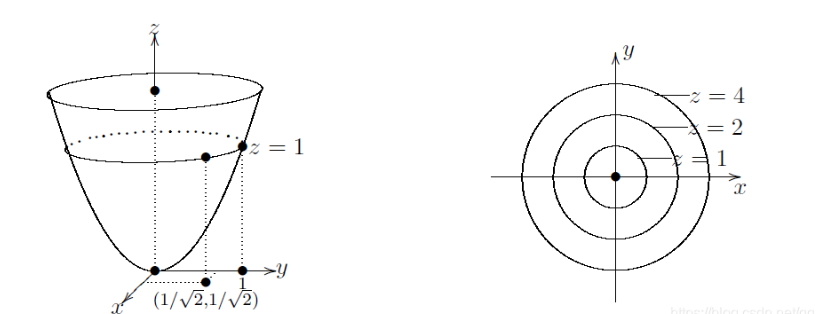
相比于原始图像,等高线图的绘制更加简单方便。但是无法精确的反应自变量的变化对因变量的影响,只能用于定性的描述这种影响是增加还是减少
2 偏导数与马鞍图
偏导数的含义很容易理解,对$x$变量的偏导描述的是,固定其他自变量后,改变$x$变量所引起的对因变量的影响。以2元函数为例,其在函数上的某一点$(x_0,y_0)$偏导值的计算方法如下: $$\frac{\partial{f}}{\partial{x}}(x_0,y_0)=lim_{\Delta x\to0 }\frac{f(x_0+\Delta x,y_o)-f(x_0,y_0)}{\Delta x}$$
偏导的几何意义:函数$z=f(x,y)$与xz平面相交于一条曲线,此线在点$(x_0,y_0)$处的切线斜率等于多元函数在此点的$x$变量偏导值
临界点(驻点):在定义域内所有偏导都为0的点
鞍点:既不是极大值点也不是极小值点的临界点
鞍点这一名称源自著名的马鞍图:
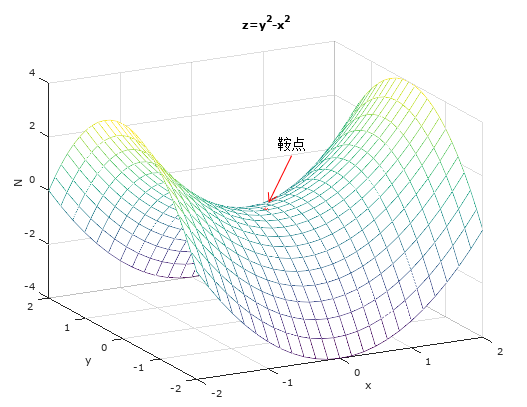
受授课内容和时长限制,本节课部分内容(切平面逼近)会在下一节课讲解
3 参考