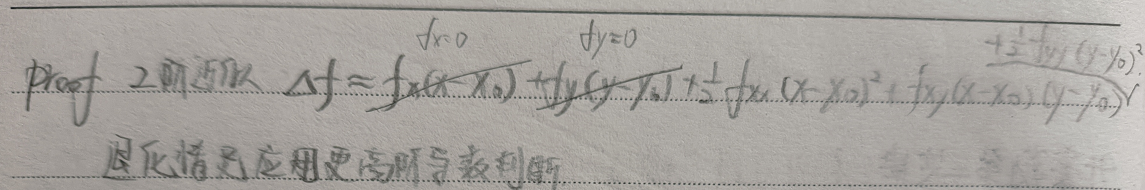1 临界点与最值
临界点共有三种可能类型:
- 局部极大值
- 局部极小值
- 鞍点
临界点的类别主要通过函数的二阶导实现判断
以$z=x^2$为例,此时$z$与$y$无关,临界点因此退化为线$x=0$
最值,即全局极大值或全局极小值,主要对比以下三种情况下的点:
- 局部极值
- 边界
- 无穷远
2 二阶导检验
设$A=f_{xx},B=f_{xy}=f_{yx},C=f_{yy}$,二阶导检验方式如下:
- $AC-B^2>0且A>0$,此时临界点为极小值
- $AC-B^2>0且A<0$,此时临界点为极大值
- $AC-B^2<0$,此时临界点为鞍点
- $AC-B^2=0$,无法判断,存在退化,需要更高阶导进行判断
由于$B^2$是非负的,所以不会存在$A=0$且$AC-B^2>0$的情况
简单证明(借助泰勒级数对函数进行二阶近似): $$\Delta f \approx f_x\Delta x+f_y\Delta y+\frac{1}{2}f_{xx}\Delta x^2+f_{xy}\Delta x\Delta y+\frac{1}{2}f_{yy}\Delta y^2$$ 由于在进行二阶导检验时,一阶偏导均等于$0$,所以上式可化简为: $$\Delta f \approx \frac{1}{2}A\Delta x^2+B\Delta x\Delta y+\frac{1}{2}C\Delta y^2$$ 令$a=\frac{1}{2}A,b=B,c=\frac{1}{2}C$,这样上式就转化为了一种常见的二元函数: $$ax^2+bxy+cy^2$$ 在$a\neq 0$的情况下,上式可以化简为两个平方和的形式: $$\frac{1}{4a}[4a^2(x+\frac{b}{2a}y)^2+(4ac-b^2)y^2]$$ 再换成$A,B,C$,可得结果: $$\frac{1}{2A}[A^2(x+\frac{B}{A}y)^2+(AC-B^2)y^2]$$ 所以上式的正负性主要取决于$A$的正负性和$AC-B^2$的正负性,得证
3 参考