1 基本概念
P问题：能在多项式时间内解决的问题，比如快速排序/冒泡排序
NP问题：能在多项式时间内验证得出一个正确解的问题（不确保在多项式时间内找到答案）
NP-Complete（NPC）问题：属于NP问题，其他所有属于NP的问题都可以规约成它
规约（Reduction）：将问题A转化为问题B，使用问题B的解来解问题A
如果问题A可规约为问题B，说明问题B的时间复杂度要大于或等于问题A的时间复杂度，即问题B的难度一般要比问题A大（毕竟B答案能解A，A不一定能解B）
规约的过程其实是将一个特殊问题一般化，将其推广为一个更有概括性、更复杂度的问题
规约具有传递性：若问题A可规约为问题B，问题B可规约为问题C，则问题A一定可规约为问题C
NP-Hard问题：不一定属于NP问题，其他所有属于NP的问题都可以规约成它
以上几种问题的关系如下图所示：
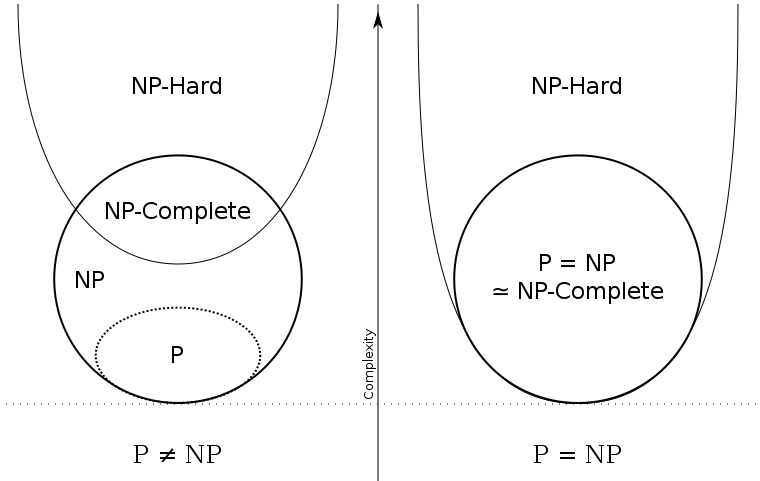
- $P\neq NP$：表示至少存在一个不可能有多项式级复杂度解法的NP问题
- $P=NP$：表示所有的NP问题都存在多项式级复杂度的解法
P/NP问题，即复杂度类P和NP是否是等价的（P=NP?）。是一个在理论信息学中计算复杂度理论领域里至今未被解决的问题，也是克雷数学研究所七个千禧年大奖难题之一
2 NP-Hard问题示例
2.1 旅行商问题
旅行推销员问题（Traveling Salesman Problem, TSP） 是一个商品推销员要去若干个城市推销商品，该推销员从一个城市出发，需要经过所有城市后，回到出发地。
旅行商问题有两个版本：
- 在一个图里，除了起始点以外不重复地遍历所有节点构成一条闭合回路，问这条回路的最短路径是多少？（如何选择行进路线使总的行程最短）---这个是最优解问题
- 在一个图里，除了起始点以外不重复地遍历所有节点构成一条闭合回路，问是否存在某条路径其长度小于特定阈值？（如何选择行进路线使总的行程小于某个值）---这个是判定性问题
2.2 哈密顿回路
哈密顿回路问题由天文学家哈密顿（William Rowan Hamilton)）提出，在一个有多个城市的地图网络中，寻找一条从给定的起点到给定的终点沿途恰好经过所有其他城市一次的路径
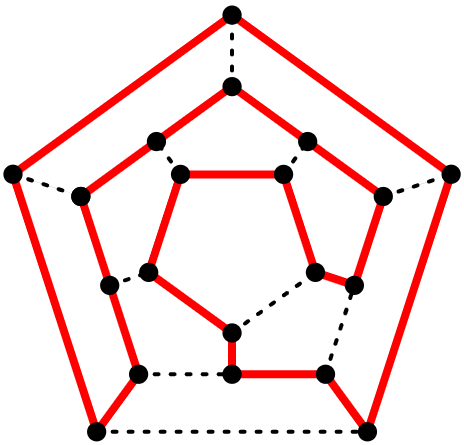
哈密顿回路问题之中的图并不要求是完全图，而当这个图的完全图并且是加权图（每个顶点之间都存在路径，并且路径存在权重/距离）时，哈密顿回路的问题就演变成了旅行商问题
3 NP-Hard问题的求解
对于最优化问题的解决方法，一般可划分以下三种：
- 确定性方法（ Exact Method）：常用于可解集较小的情况，能根据优化目标/条件/限制给出完整的解集空间（Solution Space）；比如整数规划问题（ILP）中的单纯形法，分支界定法等 #待补充
- 近似算法（ Approximate Algorithms）：在有限时间内寻找到一个有质量保证的解，通常会在理论上约束近似解与真实解间的误差（上限）；比如Christofides算法或PTAS算法
- 启发式算法（Heuristic Algorithms）：在有限时间内寻找到一个相对较好的解，但对解的质量没有保证，更多启发式算法及其细节可参阅：启发式算法总结
对于近似算法，一般使用近似比来评估算法，其值越接近1越好；比如在旅行商（TSP）问题中，近似比1.2表示该近似算法的近似解（最短路径）最多比最优解高20%
PTAS算法指的是一类多项式时间近似算法，而Christofides-Serdyukov算法是一个针对TSP问题的经典近似算法。该算法求出的近似解与实际最优解的最大近似比为1.5
更多PTAS算法可参阅论文——欧几里得旅行商及其他几何问题的多项式时间逼近方案
扩展：Christofides-Serdyukov算法
- Christofides-Serdyukov算法相当简单，至少算法运行起来很简单（感觉证明会很难）
- 把旅行商问题想象成是一个网络，每座城市就是一个节点，两两城市之间的路径就是一条边。每条边对应一定的成本，比如城市之间的旅行时间或者距离
- Christofides-Serdyukov算法首先选择能够连接所有城市同时花费最小的边集（只需不断添加新城市，且满足花费最少即可，但这不是最终解）
- 连接完所有城市后，有些城市可能会出现奇数条边，这是错误的，因为每次通过一条边进入一个城市，那么也一定会通过另一条对应的边离开它。因此，算法随后会添加成本最低的边集，使得每座城市都有偶数条边，据此产生最终路径
Christofides-Serdyukov算法依赖于图论中的欧拉路属性
对于NP-Hard问题的解决方法：
- 一般不能用确定性方法求解，但通过增加约束对问题进行简化
- NP-Hard问题有时可以使用近似算法进行求解， 但仅限特定问题
- 在许多情况下，用启发式方法来解决 NP-Hard问题是合理的