个人笔记

特征值与特征向量

浓缩矩阵的信息 ../../../1_study/math/线性代数基础

特征值、特征向量、谱定理、矩阵的快速幂、SVD

以上算是PCA的相关数学基础

PCA其中变量解耦的过程是值得衍生到其他领域的

投资组合风险控制

$$ \mathop{min}\limits_{w} (Risk) = w^T \Sigma w$$ $$ s.t. \ w_1+...w_n=1$$

• $\Sigma$表示投资组合的协方差矩阵
• $w$表示投资组合中各证券的权重

求解方式有两种：

1. 线性代数法：寻找最小特征值对应的特征向量
2. 最优求解法：利用拉格朗日乘子法进行求解

数据集：推荐80%历史数据+20%预测数据 详情

随机矩阵理论 random matrix theory

Marchenko-Pastur distribution 描述随机矩阵的特征值分布 详情

根据以上分布，限定一个均值范围内的区间，进而删除范围内的特征值

此时的特征值删除相当于去除了投资组合中的随机因素

比如均值是0.5，删除特征值在0.2到0.8之间的情况，仅保留极端的非常态特征，然后根据过滤后的证券，建立新的资产组合，再次计算$\Sigma$和$w$，并寻找最小风险的组合。

以上过程给我的感觉有点类似于NLP过程中通过删除常用词而保留低频词，进而提纯文本的特征。

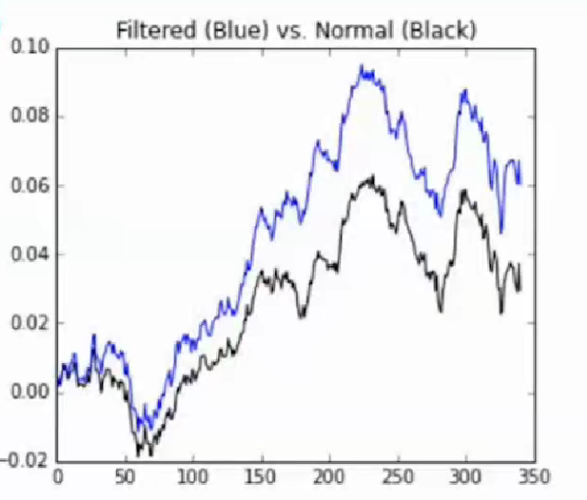
有过滤的最小风险投资组合vs没过滤的最小风险投资组合

课程推荐

MIT 线性代数 Stanford 凸优化（convex optimization）

论文速读

标题：Classification-based Financial Markets Prediction using Deep Neural Networks 日期：2016-03-30

特点：

• 利用五分钟一次提取的高频数据，构建了9895个特征
• 利用高性能处理器进行RNN神经网络训练
• 最终结果得到了不错的夏普值。

标题：Deep Learning for Multivariate Financial Time Series 日期：2016-06-04

特点：

• 特征比较简单，日收益和月收益
• 基于DBN模型进行建模
• 最终错误率为46%，低于传统算法的50%

标题：欧盟央行出品的quant报告-市场情绪与网络文本 日期：2015-07-09

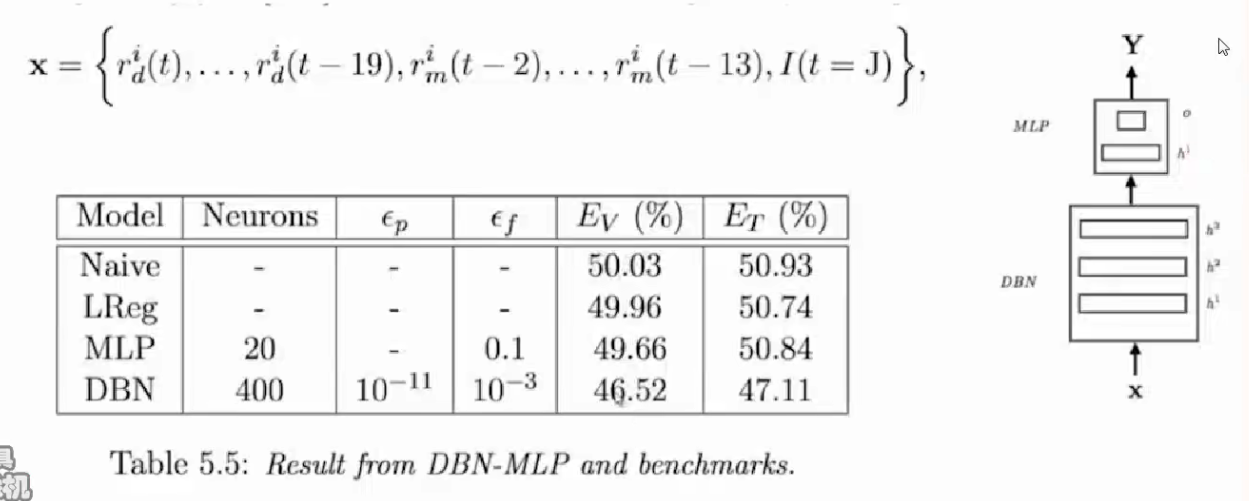
特点：

• 推特和谷歌所涉及的投资者相关信息是衡量情绪的重要指标
• 每周的推特市场情绪（bullishness）和谷歌市场情绪存在正相关性
• 这两类市场情绪与其他机构（the Daily Sentiment index、the US Advisors's Sentiment Report of investors Intelligence）所得的情绪存在正相关性
• 这两类市场情绪每日波动要优先于实际市场（如美国、英国、加拿大等国家的重要指数）的波动，但是不适应于中国市场。但是微博之类的可以~

标题：Predictive analysis of financial time series 日期：2015-06-04

特点：

• 建立了多种量化指标及其衍生

通过多种模型（KNN、LogisticRegression、SVM、RandomForest）进行回测