1 基本概念
蚁群算法(Ant Colony Algorithm,ACA)由Marco Dorigo于1992年在他的博士论文中首次提出,该算法模拟了自然界中蚂蚁的觅食行为。
蚂蚁寻径的生物过程:
- 蚂蚁在寻找食物源时,会在其经过的路径上释放一种信息素,并能够感知其它蚂蚁释放的信息素。信息素浓度的大小表征路径的远近,信息素浓度越高,表示对应的路径距离越短
- 通常,蚂蚁会以较大的概率优先选择信息素浓度较高的路径,并释放一定量的信息素,以增强该条路径上的信息素浓度,这样,会形成一个正反馈
- 最终,蚂蚁能够找到一条从巢穴到食物源的最佳路径,即距离最短
- 值得一提的是,生物学家发现,路径上的信息素浓度会随着时间的推进而逐渐衰减
2 核心过程
ACA算法解决优化问题的基本思路:
- 用蚂蚁的行走路径表示待优化问题的可行解,整个蚁群的所有路径构成待优化问题的解空间
- 路径较短的蚂蚁释放的信息素量较多,随着时间的推进,较短的路径上累积的信息素浓度逐渐增高,选择该路径的蚂蚁个数也愈来愈多。最终,整个蚂蚁会在正反馈的作用下集中到最佳的路径上,此时对应的便是待优化问题的最优解
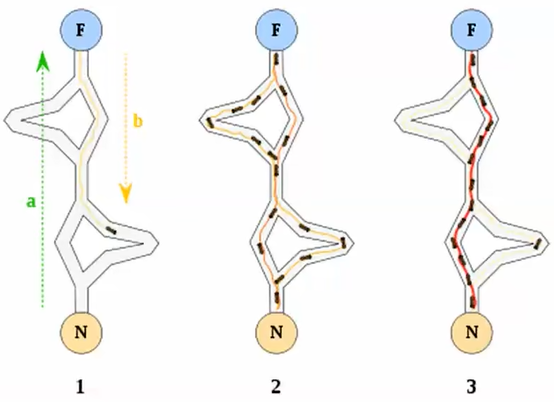
ACA算法核心过程:
- 假设蚁群数量为$m$,城市数量为$n$,任意两个城市间的距离为$d_{ij}(i,j=1,2,...,n)$
- 在$t$时刻城市$i$和城市$j$间路径上的信息素浓度为$\tau_{ij}(t)$,各城市间初始信息素浓度相同$\tau_{ij}(0)=\tau_0$
- 设$P^k_{ij}(t)$表示蚂蚁$k$在时刻$t$从城市$i$转移到城市$j$的概率,其计算公式如下:
$$P^k_{ij}(t) = \frac{[\tau_{ij}(t)]^\alpha[\eta_{ij}(t)]^\beta}{\Sigma_{s \in S_k}[\tau_{is}(t)]^\alpha[\eta_{is}(t)]^\beta} $$
- 其中$\eta_{ij}(t)$为启发函数,表示蚂蚁从城市$i$转移到城市$j$的期望度;常设$\eta_{ij}(t)=1/d_{ij}$
- $S_k$为蚂蚁$k$待访问城市的集合。开始时,$S_k$中有$(n-1)$个元素,即包括除了蚂蚁$k$出发城市的其它所有城市。随着时间的推进,$S_k$中的元素不断减少,直至为空,即表示所有的城市均访问完毕
- $\alpha$为信息素重要程度因子,其值越大,表示信息素的浓度在转移中起的作用越大
- $\beta$为启发函数重要程度因子,其值越大,表示蚂蚁会以较大的概率转移到距离短的城市
- 当所有蚂蚁完成一次循环后,各城市间路径上的信息素浓度需进行更新,具体公式如下:
$$\begin{equation} \left\{ \begin{gathered} \Delta\tau_{ij}^k=Q/L_k \ \\ \Delta\tau_{ij}=\Sigma_{k=1}^n\Delta\tau_{ij}^k \ \\ \tau_{ij}(t+1)=(1-\rho)\times \tau_{ij}(t)+\Delta\tau_{ij}
\end{gathered}
\right. \end{equation}$$
- 其中,$Q$表示蚂蚁循环一次释放的信息素总量(常数)
- $L_k$表示第$k$只蚂蚁从城市$i$访问城市$j$期间经过路径的长度
- $\Delta\tau_{ij}^k$表示第$k$只蚂蚁在城市$i$与城市$j$连接路径上释放的信息素浓度
- $\Delta\tau_{ij}$表示所有蚂蚁在城市$i$与城市$j$连接路径上释放的信息素浓度之和
- 参数$\rho(0<\rho<1)$表示信息素的挥发程度,模拟信息素随着时间推移而消散的过程
3 算法分析
ACA算法的特点:
- 采用正反馈机制,使得搜索过程不断收敛,最终逼近于最优解
- 个体通过释放信息素来改变周围的环境,并且个体能够感知周围环境的实时变化,因此个体间可以通过环境进行间接的信息交流
- 搜索过程采用分布式计算方式,不同个体可以并行计算,算法的计算能力和运行效率好
- 启发式的概率搜索方式,不容易陷入局部最优,易于寻找到全局最优解
4 代码实现
基于scikit-opt包的Python实现——解决旅行商问题:
import numpy as np
from scipy import spatial
import pandas as pd
import matplotlib.pyplot as plt
num_points = 25
points_coordinate = np.random.rand(num_points, 2) # generate coordinate of points
distance_matrix = spatial.distance.cdist(points_coordinate, points_coordinate, metric='euclidean')
def cal_total_distance(routine):
num_points, = routine.shape
return sum([distance_matrix[routine[i % num_points], routine[(i + 1) % num_points]] for i in range(num_points)])
from sko.ACA import ACA_TSP
aca = ACA_TSP(func=cal_total_distance, n_dim=num_points,
size_pop=50, max_iter=200,
distance_matrix=distance_matrix)
best_x, best_y = aca.run()
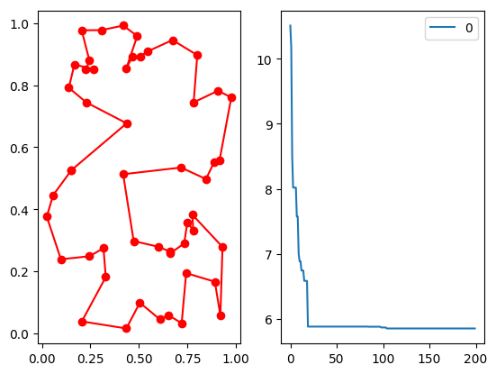
fig, ax = plt.subplots(1, 2)
best_points_ = np.concatenate([best_x, [best_x[0]]])
best_points_coordinate = points_coordinate[best_points_, :]
ax[0].plot(best_points_coordinate[:, 0], best_points_coordinate[:, 1], 'o-r')
pd.DataFrame(aca.y_best_history).cummin().plot(ax=ax[1])
plt.show()