1 散度定理的理解
在上一课时中,对于$\vec{F}=<P,Q,R>$的三维向量场,提出了散度定理: $$∯_S<P,Q,R>\cdot \hat{n}dS=\int \! \! \!\int \! \! \!\int_D (P_x+Q_y+R_z)dV$$
定义三维空间下的$Del$算子:$\nabla=<\partial{}/\partial{x},\partial{}/\partial{y},\partial{}/\partial{z}>$
对于普通三元函数$f$,$\nabla{f}=<f_x,f_y,f_z>$表示函数的梯度
对于三维向量场$\vec{F}$,$\nabla{\vec{F}}=<\partial{}/\partial{x},\partial{}/\partial{y},\partial{}/\partial{z}>\cdot <P,Q,R>=<P_x,Q_y,R_z>$表示散度
散度的其他理解,可参考定义格林公式时的散度理解
2 散度定理的证明:
由于向量场在$<P,Q,R>$三个方向上的证明是独立的,因此散度定理的证明只需要其在一个方向上成立即可,比如:$∯_S<0,0,R>\cdot \hat{n}dS=\int!!!\int!!!\int_D R_zdV$
将闭合曲面$S$围成的空间$D$进行竖直切分,切分成$n$个小的曲面$s'$围成的空间$d'$, 则这$n$个小曲面$s'$的面积分之和将等于大曲面$S$的面积分;$n$个小空间$d'$的三重积分之和将等于大空间$D$的三重积分,因此散度定理只需要在小曲面$s'$和小空间$d'$上成立即可
小曲面$s'$可简单拆分成底面、顶面、侧面三个部分,由于只需证明公式在方向$R$上成立,而竖直切分得到的小曲面$s'$可近似看作垂直的,其面的法向量$\hat{n}$与向量场$<0,0,R>$是垂直的,因此二者的乘积恒为$0$,在证明中可忽略
散度定理的证明经过三次简化,只需证明公式在向量场$<0,0,R>$、小曲面$s'$和小空间$d'$上成立,同时计算面积分时可忽略曲面侧面,只需计算底面和顶面的面积分
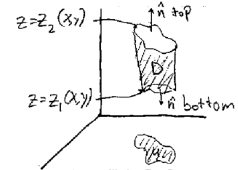
假设曲面的底面函数为$S_底=z_1(x,y)$,曲面的顶面函数为$S_顶=z_2(x,y)$,底面和顶面在$xy$面上的投影为$U$(侧面是垂直的,因此两个面的投影是一样的)
则顶面的面积分等于(可直接套用上一课的通量计算公式):
$$∯_{顶}<0,0,R>\cdot \hat{n}dS=\int \! \! \!\int_{顶} Rdxdy=\int \! \! \!\int_UR(x,y,z_2)dxdy$$
同理,底面的面积分结果为:
$$∯_{底}<0,0,R>\cdot \hat{n}dS=\int \! \! \!\int_{底} Rdxdy=-\int \! \! \!\int_UR(x,y,z_1)dxdy$$
小曲面$s'$的最终面积分便是以上二者的加和:
$$
\begin{align}
∯_S<0,0,R>\cdot \hat{n}dS & =\int \! \! \!\int_U[R(x,y,z_2)-R(x,y,z_1)]dxdy
\ \\
& = \int \! \! \!\int_U\int_{z_1}^{z_2} R_zdxdydz
\ \\
& =\int \! \! \!\int \! \! \!\int_D R_zdV
\end{align}
$$
得证
3 散度定理的应用
扩散方程:描述烟雾/颜料在空气/溶液中的运动
假设时刻$t$时某一点的浓度为$u=u(x,y,z,t)$,则浓度的扩散过程满足以下方式: $$\frac{\partial{u}}{\partial{t}}=k\nabla^2u=k(\frac{\partial^2{u}}{\partial{x}^2}+\frac{\partial^2{u}}{\partial{y}^2}+\frac{\partial^2{u}}{\partial{z}^2})$$ 其中$\nabla^2$是指$u$的拉普拉斯算子;此方程也可用于描述温度的变化(热扩散)
颜料总是从浓度高的地方流向浓度低的地方,并且浓度差越大,颜料的流动越快,所以描述这种流动的向量场可定义如下:$\vec{F}=-k\nabla u$
此时,原始的扩散方程可拓展成如下形式: $$\frac{\partial{u}}{\partial{t}}=-div(\vec{F})=+kdiv(\nabla u)=k\nabla^2u$$
以上公式展现了理解散度意义的另一种方式
4 参考

