1 通量
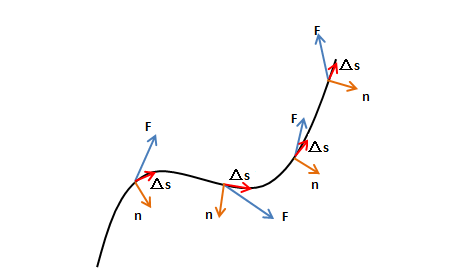
通量衡量沿着曲线前进时通过曲线的向量场多少，也可以用于描述单位时间内流体场$\vec{F}$通过曲线$C$的流量： $$∮_c\vec{F}\cdot \hat{n}ds$$
其中$\hat{n}$就是曲线$C$各点处的单位法向量（前进方向的右侧，右正左负是一种约定成俗）
2 通量的简单计算
部分情况下，可根据通量的定义进行直接计算
假设曲线$C$是圆心在原点，半径为$r$的逆时针旋转得到圆
情况1：$\vec{F}//\hat{n}$，可假设$\vec{F}=<x,y>$
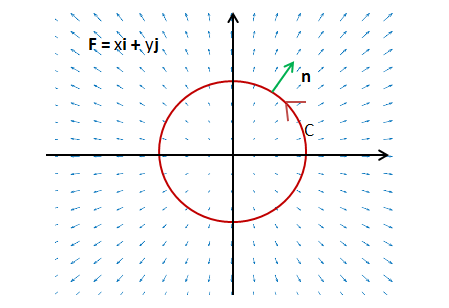$$∮_c\vec{F}\cdot \hat{n}ds=∮_c|\vec{F}||\hat{n}|cos\theta ds=∮_cr ds=2\pi r^2$$
情况1：$\vec{F}\perp \hat{n}$，可假设$\vec{F}=<-y,x>$
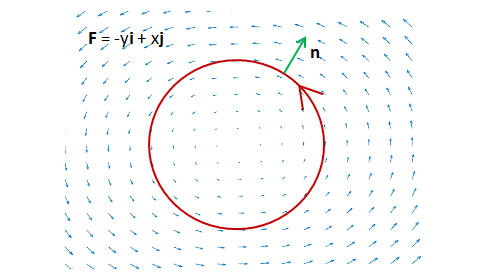$$∮_c\vec{F}\cdot \hat{n}ds=0$$
3 通量与线积分
思考之前线积分的物理意义（做功），其标准线积分形式如下： $$W=∮_c\vec{F}\cdot d\vec{r}=∮_c\vec{F}\cdot \hat{T}ds$$ 其中$\hat{T}$是曲线$C$各点处的单位切向量，而$\hat{T}$顺时针旋转$90°$就是$\hat{n}$，二者关系如下： $$\hat{T}ds=<dx,dy>,\hat{n}ds=<-dy,dx>$$ 所以通量其实也是一种线积分，二者的物理含义不同，但是计算形式是一致的： $$∮_c\vec{F}\cdot \hat{n}ds=∮_c<M,N>\cdot <-dy,dx>=∮_cMdy-Ndx$$
4 完整的格林公式
通量作为一种线积分，满足假设条件时可以进行格林公式进行计算的转换： $$∮_cMdy-Ndx=\int \! \! \!\int_R(M_x+N_y)dA=\int \! \! \!\int_Rdiv(\vec{F})dA$$ 类比于旋度的计算，此处存在散度的定义： $$div(\vec{F})=M_x+N_y$$
散度描述的是一种流体的发散程度，可以描述流体膨胀后的空间占用，也可以描述一种”源头“的冒出率。此处可以联想化学实验中气体生成并充斥于容器的过程，也可以联想泉水涌出形成河流的过程
完整的格林公式： $$ \begin{equation} \left\{ \begin{gathered} ∮_cMdy-Ndx=\int \! \! \!\int_Rdiv(\vec{F})dA=\int \! \! \!\int_R(M_x+N_y)dA \ \\ ∮_cMdy+Ndx=\int \! \! \!\int_Rcurl(\vec{F})dA=\int \! \! \!\int_R(N_x-M_y)dA \end{gathered} \right. \end{equation} $$
关于旋度和散度的可视化思考可参阅3Blue1Brown的视频《散度与旋度》
5 参考
