1 平面向量场
向量场(vector fields)将空间中的点映射为向量,用于描述空间流体或力的强度和方向
常见的向量场举例:风场、引力场、电磁场、水流场
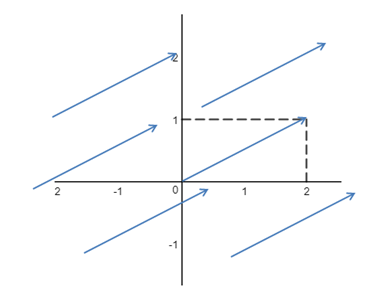
假设存在函数$M(x,y)$和$N(x,y)$,用$\vec{F}$来描述向量场: $$\vec{F}=M\vec{i}+N\vec{j}$$ 示例1:$\vec{F}=2\vec{i}+\vec{j}$,其向量场可视化结果如下:
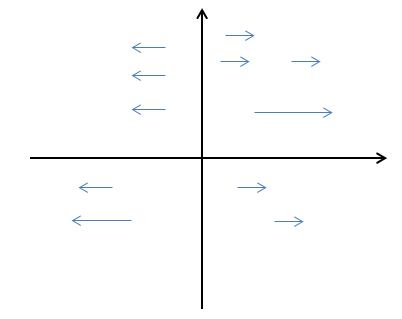
示例2:$\vec{F}=x\vec{j}$,其向量场可视化结果如下:
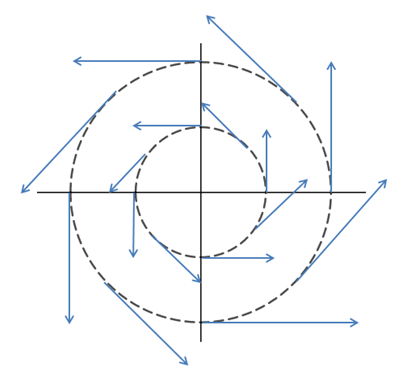
示例3:$\vec{F}=-y\vec{i}+x\vec{j}$,其向量场可视化结果如下:
2 功与线积分
在物理学中,做功等于力与力方向上位移的乘积:$W=\vec{F}\cdot \Delta {\vec{r}}$
由于实际中的力场往往是不均衡的,所以做功的计算需要通过线积分的形式求解: $$W=\lim_{\Delta \vec{r}\to0}\Sigma_i\vec{F}\cdot \Delta {\vec{r_i}} =\int_c \vec{F}\cdot d\vec{r}=\int_{t_1}^{t_2}\vec{F}\cdot \frac{d\vec{r}}{dt}dt$$ 例题:计算函数$\vec{F}=-y\vec{i}+x\vec{j}$在$c:x=t,y=t^2(0\leq t\leq 1)$上的线积分
解法1:直接套用公式,进行向量计算 $$\int_c \vec{F}\cdot d\vec{r}=\int_0^1\vec{F}\cdot \frac{d\vec{r}}{dt}dt=\int_0^1<-t^2,t>\cdot <1,2t>dt=\frac{1}{3}$$ 解法2:考虑向量场定义,$\vec{F}=<M(x,y),N(x,y)>$ $$\int_c \vec{F}\cdot d\vec{r}=\int_cM(x,y)dx+N(x,y)dy$$ 带入$x=t,y=t^2$,可得结果:
$$\int_0^1-t^2dt+t\times 2tdt=\frac{1}{3}$$
3 参考