前置知识:图论基础
代码实践:图特征工程_Python实现
节点中心性度量
度中心性 (Degrree Centrality):
- 用节点的度来描述节点的重要性,即邻接节点数越多的节点越重要
- 在不同网络间比较时,需要除以网络总节点数进行标准化
特征向量中心性 ( Eigenvector Centrality): $$ c_v=\frac{1}{\lambda}\sum_{u\in N(v)}c_u $$
- 节点的重要性取决于邻接节点的重要性之和
- 其本质对应一个图邻接矩阵的特征向量求解问题
介数中心性 (Betweenness Centrality): $$ c_v=\sum_{s\neq v\neq t}\frac{#(\text{shortest paths betwen}s\text{and}t\text{that contain}v)}{#(\text{shortest paths between}s\text{and}t)} $$
- 任意节点间最短路径中存在该节点的比例
- 介数中心性可以用来识别在网络中具有很高控制力的节点
- 例如交通网络中的关键路口或生物网络中的重要基因
紧密中心性 (Closeness Centrality): $$c_v=\frac1{\sum_{u\neq v}\text{ average/shortest path length between }u\ \text{and}\ v}$$
- 一个节点到其他节点的平均距离的倒数
- 紧密中心性反应了该节点到其他节点的综合便捷程度
集群系数
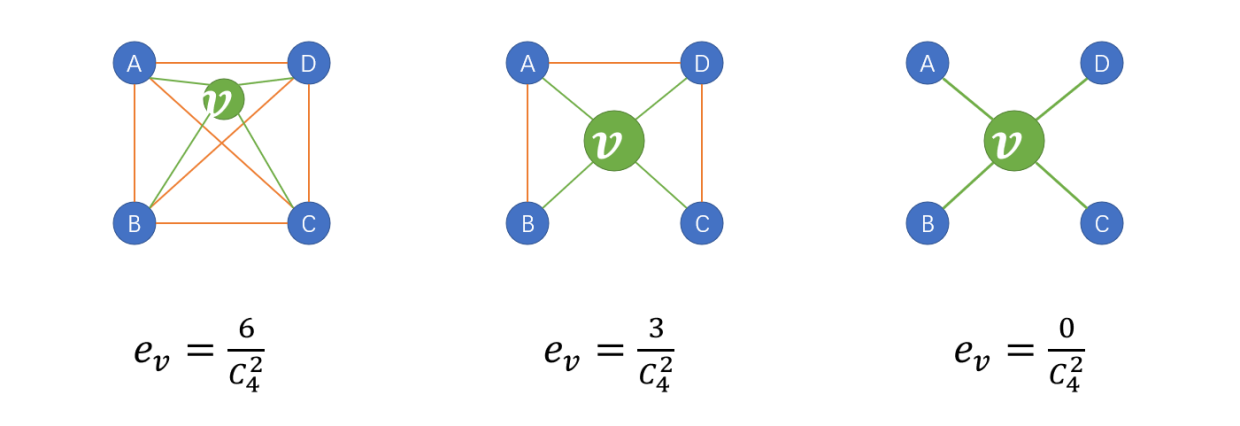
集群系数 (Clustering Coefficient): $$ e_v=\frac{#(\text{edges among neighboring nodes})}{\binom{k_v}2}\in[0,1] $$
- 邻接节点间的连接数/邻接节点间所有可能的连接数
- 该指标用于衡量图中节点的聚集成团的程度
- 节点的集群系数越高,说明其邻接节点越密切
集群系数的计算举例:
异构连通子图 Graphlets
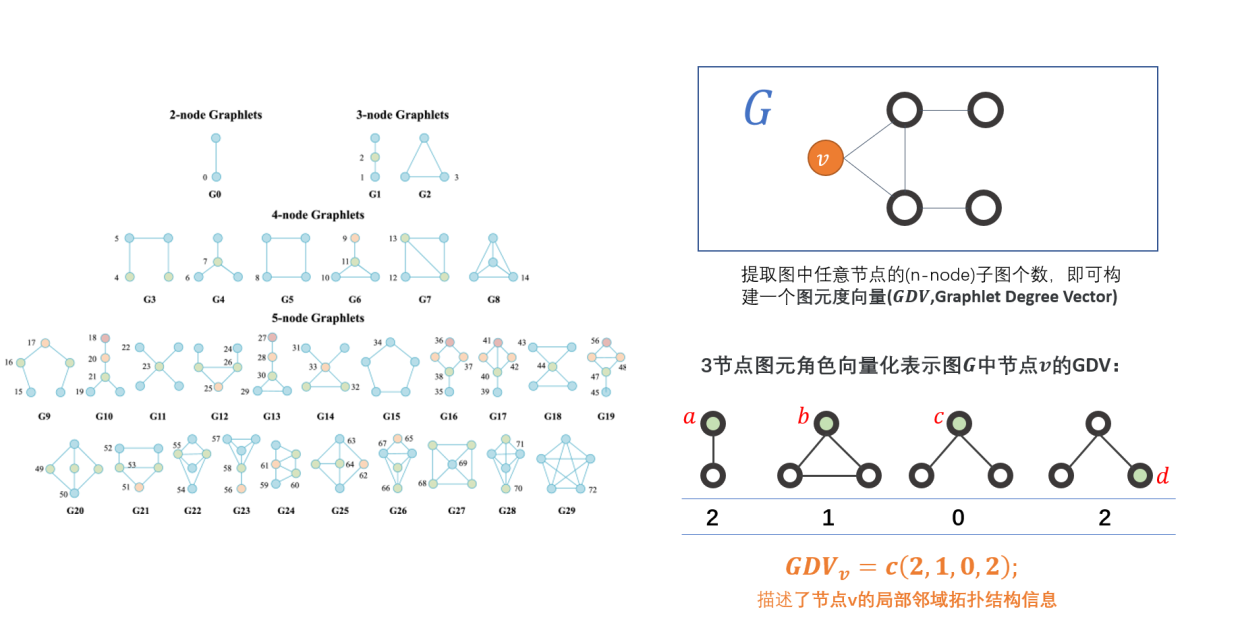
异构连通子图(graphlets,也称图元):指图网络中大量重复存在的小型拓扑结构
图元度向量(Graphlet Degree Vector,GDV):对图中的图元(Graphlet)进行计数从而得到图的特征向量表示,GDV 可以用于衡量节点或图的相似性
 Graphlet 分析的作用:
Graphlet 分析的作用:
- 发现社交网络中的社区结构和关键节点
- 帮助发现蛋白质复合物和信号通路等功能模块
- 深入神经网络中的模式和规律,进而理解神经的功能和行为
WL 图同构检验
Weisfeiler-Lehman 算法是检验图同构的经典算法
WL 检验结果是图同构的必要不充分的条件:
- 当 WL 检验结果显示两个图有差异时,可认为这两个图是非同构的
- 当 WL 检验结果显示没有差异时,只能认为这两个图可能是同构的
WL 检验的计算过程:
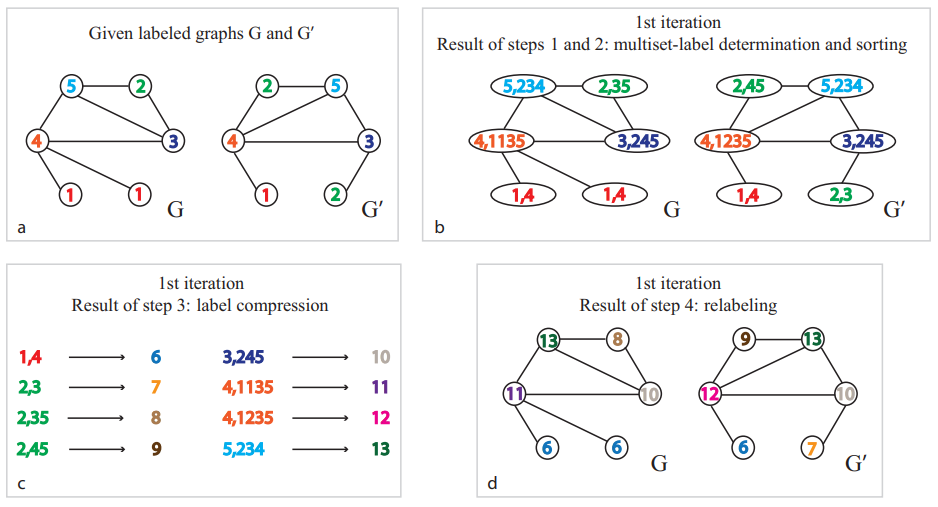
- (a)给定两个图,确保每个节点都有标签(没有标签时可用节点的度来替代)
- (b)考虑各个节点的 1 跳邻居节点,构建邻域节点排序后的多重集(multi-sets)
- (c)对标签进行压缩映射(hash 或数字编号),将多重集映射为一个简短标签
- (d)将压缩映射后的新标签更新到各个节点上,重复以上过程直到标签稳定不变
步骤(b)中,排序的作用是保证结果不会受到节点顺序的影响
结果判定:如果两个图相同标签的出现次数不一致,即可判断两个图不同构
第 $k$ 次迭代后的节点标签表示了高度为 $k$ 的节点子树结构(WL subtree)
当两个节点的标签一样时,表示分别以这两个节点为根节点的 WL 子树是一致的