首先,理解梯度向量是指向函数值增长最快的方向的:MIT18.02笔记-梯度的定义与理解
定义函数$f(x)$,其在点$x$处沿着方向$d$的变化率可用方向导数表示,即梯度与方向的乘积: $$Df(x;d)=\nabla f(x)^Td$$ 当$d=-\frac{\nabla f(x) }{ ||\nabla f(x)|| }$时,函数$f$在点$x$处的下降速率最大,即负梯度方向为最速下降方向
最速下降算法:在迭代过程,每次都选择负梯度方向搜索(对于寻找最小值的最优化问题)
最速下降算法步骤:
- 初始化$x_1$,设定允许的最小误差$\epsilon$,迭代次数$k=1$
- 对于第$k$次迭代,计算得出最速下降方向:$d_k=-\nabla f(x_k)$
- 当$||d_k||\leq \epsilon$或迭代次数达到上限时,算法结束;否则进入步骤4
- 从点$x_k$出发,沿着方向$d_k$展开一维搜索,找到最优的步长$\lambda_k$:
$$argmin_{\lambda_k}f(x_k+\lambda_kd_k)$$ 5. 更新坐标与迭代次数:$x_{k+1}=x_k+\lambda_k d_k,\ \ k=k+1$,并进入步骤2
最优的步长$\lambda_k$的确定:
- 微分法,针对正定二次目标函数,$argmin_{\lambda_k}f(x_k+\lambda_kd_k)$对应着梯度为0时的取值
- 通过一维寻优法(相当于优化版的遍历查找),比如黄金比例法或者斐波那契法
最速下降算法图示:
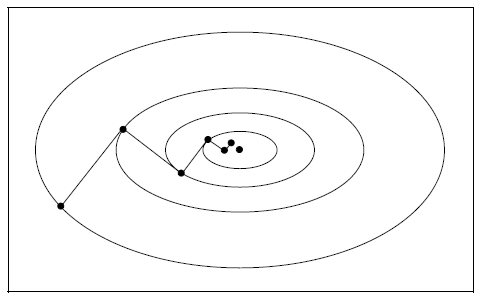
证明:最速下降法相邻两次的搜索方向正交(重要结论)
- 假设目标函数为正定二次,利用微分法求解$argmin_{\lambda_k}f(x_k+\lambda_kd_k)$
- 最优的$\lambda_k$取值对应着下式的求解: $$\frac{\partial{f(x_k+\lambda_kd_k)}}{\partial{\lambda_k}}=0$$
- 转换上式为如下形式:
$$\frac{\partial{f(x_k+\lambda_kd_k)}}{\partial{\lambda_k}}=\frac{\partial{(x_k+\lambda_kd_k)}}{\partial{\lambda_k}}\frac{\partial{f(x_k+\lambda_kd_k)}}{\partial{(x_k+\lambda_kd_k)}}=d_k\nabla f(x_{k+1})=0$$
- 由于第$k+1$次迭代的方向为$-\nabla f(x_{k+1})$,所以可以得出$d_k$和$d_{k+1}$是正交的
微分法计算步长$\lambda_k$:
- 假设目标函数为正定二次函数:$f(x)=\frac{1}{2}x^TGx+b^Tx+c$
- 则$\nabla f(x_{k+1})=Gx_{k+1}+b=G(x_k+\lambda_k d_k)+b=\nabla f(x_{k})+G\lambda_k d_k$
- 上式两边同时乘以$d_k$以利用最速下降法的重要性质(相邻两次的搜索方向正交): $$d_k^T \nabla f(x_{k+1})=d_k^T \nabla f(x_{k})+d_k^TG\lambda_k d_k=0$$
- 上式化简后,即可得到步长$\lambda_k$的解析解: $$\lambda_k=-\frac{d_k^T \nabla f(x_{k})}{d_k^TG d_k}$$
最速下降算法分析:
- 理论明确,计算简单,对初始位置不敏感
- 收敛速度很慢,越靠近极小点步长越小
最速下降法 vs 梯度下降法
- 两种算法非常相似:都利用梯度信息,通过迭代式搜索来逐步逼近最优解
- 但梯度下降法中的步长是固定的,而最速下降法的步长会自动寻找合适值
- 更抽象地来理解,梯度下降法是最速下降法在欧式范数情况下的一个特例
- 因为对于其他范数标准(如矩阵2-范数),负梯度并不总是指向标准的最速下降方向
更多细节可参阅: