中文标题:Capsules与自编码器变体
英文标题:Transforming Auto-Encoders
发布平台:ICANN
Artificial Neural Networks and Machine Learning – ICANN 2011
发布日期:2011-01-01
引用量(非实时):1434
DOI:10.1007/978-3-642-21735-7_6
作者:Geoffrey E. Hinton, Alex Krizhevsky, Sida D. Wang
文章类型:bookSection
品读时间:2022-03-30 09:48
1 文章萃取
1.1 核心观点
本文借鉴特征算法SIFT中包含姿态等丰富信息的向量输出,通过对普通神经网络的标量输出进行改进,构建了基于“胶囊”结构的自编码器变体,实现了具备视觉不变性的的优质特征提取
1.2 综合评价
- 本文对于“胶囊”结构的思考深刻而丰富,展现了完整的思维链
- 不同于传统神经网络的标量输出,“胶囊”的输出特征更符合视觉逻辑
- 通过对于自编码器的巧妙改造,“胶囊”的输出特征能实现丰富的图像属性表达
- 通过多层次的实验对比,展现出来“胶囊”的输出特征强大的泛化能力
- 行文逻辑清晰但是实验细节存在缺失,十分影响阅读体验
1.3 主观评分:⭐⭐⭐⭐
本文作为Capsules网络的“前传”,对Capsule的本质有着更深刻的思考,继承了可信网络中对于图像的层次抽象与视觉不变性的思考,又结合了能力更强的神经网络算法与CNN网络结构,使得最终的“胶囊”学习到了一些较为惊艳的特性,也为后来的Capsules网络的诞生埋下了伏笔。
2 精读笔记
2.1 背景介绍
卷积神经网络(CNN)的局限性:
- 通过池化层实现了局部的平移不变性(local translational invariance),但是CNN无法掌握图像中物体的整体与局部之间的精准空间关系
- 因为多次下采样,导致神经网络深层中的抽象特征存在很大的不确定性
- 神经元的输出为单一标量,难以实现视觉上的不变性(viewpoint-invariant)
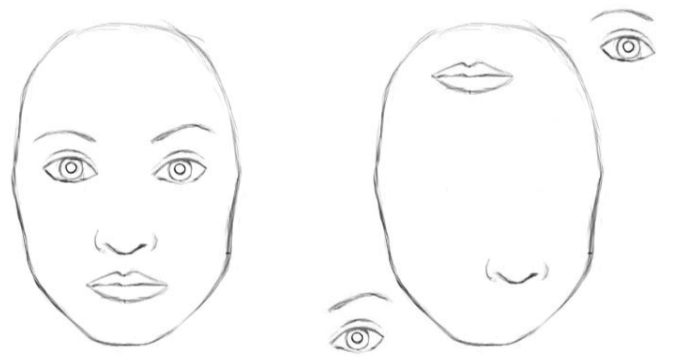
再考虑传统计算机视觉中的常用特征算法,比如SIFT算法,此类特征算法最终能输出一个具备视觉不变性的向量。借鉴这类特征算法的思想并考虑CNN的局限性,本文提出了局部"胶囊(capsules)"的概念。
这些”胶囊“可以对输入完成复杂的内部计算,并将结果封装到一个高信息密度的向量中。每个”胶囊“学习的是视觉实体的某些隐式定义(比如姿态、光照、形变),“胶囊”的输出可以是这类实体出现的概率,也可以是描述实体属性的实例化参数。
假设两个”胶囊“的输出分别表示嘴巴和鼻子的实例化参数,二者可以通过坐标变换(用权重矩阵描述)建立空间关系,这就实现了对图像层次的抽象理解,而嘴巴和鼻子一定是在正确的空间关系中才形成的一张脸。
2.2 自编码变体
背景知识补充:自编码器
为了方便理解并简化问题,本小节先只考虑平移这一种状态变换,自编码器变体的作用就是根据输入图像进行编码,并根据平移信息解码出平移后的图像。
自编码器变体主要由”胶囊“组成,每个”胶囊“都有独立的识别神经元(recognition units,相当于自编码器中的编码器)和生成神经元(generation units,相当于自编码器中的解码器)
以三个“胶囊”构建的自编码器变体为例:
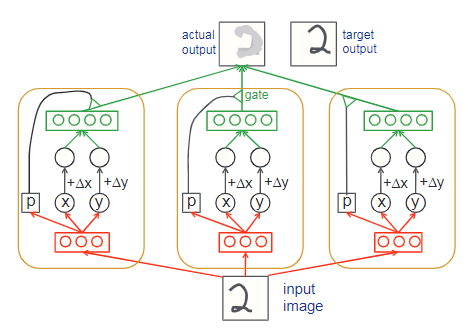
- 其中每个”胶囊“包含3个识别神经元和4个生成神经元
- 图像输入与目标图像存在平移,同时对编码结果进行相同的平移操作
- 每个”胶囊“会根据输入的识别神经元计算概率$p$
- 概率$p$用于判断此”胶囊“的生成神经元是否参与最终的结果计算
如果把编码结果看作隐式特征,则自编码器变体得到的特征将具备平移不变性
2.3 实验与结论
2.3.1 仅考虑平移
第一阶段的实验主要构建了30个“胶囊”用于组成自编码器变体,每个“胶囊”包含10个识别神经元和20个生成神经元。以MINIST手写数字识别数据集作为训练集,平移操作在$x$方向和$y$方向都有五种:进行$-2,-1,0,1,2$个像素的随机移动。最终得到的自编码器变体结果如下所示:
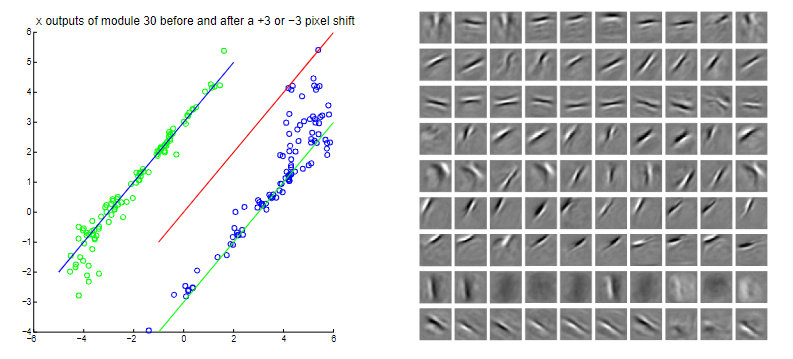
左图说明:选择一个特定的“胶囊”,并观察此“胶囊”的$x$神经元输出。纵坐标表示无平移图像输入“胶囊”后所得到的$x$神经元输出,横坐标表示平移$-3$或$3$个像素点后的图像输入“胶囊”后所得到的$x$神经元输出。直线为用作观测的辅助线。
可得结论:
- $x$神经元输出随着输入的平移而进行相应平移,说明了特征具备平移不变性
- “胶囊”的平移不变性存在扰动的情况,对极端取值不适用,但可以通过$gate$规避
右图说明:选择9个“胶囊”并对其中的前10个生成神经元权重进行可视化
可得结论:
- 图像显示自编码器变体学到了类似于“横竖撇捺”的特征信息
- 这类特征具备平移不变性,并初步归纳出了图像层次的抽象信息
2.3.2 更复杂二维变换
背景知识:图像几何变换
第二阶段的实验主要构建了25个“胶囊”用于组成自编码器变体,每个“胶囊”包含40个识别神经元和40个生成神经元。除此之外,最重要的是将上一节中的平移变换转为二维仿射变换(包含平移、旋转、缩放、裁剪等操作,具体可用$3\times 3$的变换矩阵$T$实现),则原本每个“胶囊”的编码(神经元$x$和神经元$y$)也需要转变为$3\times 3$的矩阵$A$,$TA$(类比于上一节中的$x+\Delta x$,$A$也需要进行相同的仿射变换)将用作生成神经元的输入并用于生成最终的解码图像,结果如下:

说明:第一行表示原始图像,第二行表示解码图像,即自编码器的最终解码输出,第三行表示目标图像,即原始图像经过某种仿射变换后得到的图像
对前7个"胶囊"的前20个生成神经元权重进行可视化:

2.3.3 考虑三维视角
第三阶段的实验主要构建了900个“胶囊”用于组成自编码器变体,用于应对三维图像的复杂结构,每个“胶囊”也进行了更为复杂化的处理(此处论文描述略显含糊,大致的意思就是借助感受野和步长,每个“胶囊”只专注于局部的图像复原,并最终把所有的局部图像拼凑回完整图像,具体细节不再深究)
实验效果如下所示:

左图说明:第一列表示输入图像,第二列表示解码图像,第三列表示目标图像
右图说明:同左图,但是右图中的小车模型并不在训练集范围内(泛化能力强)
2.3.4 总结
每个“胶囊”只能表示实体的一种实例化参数,但是真实的实体构成是层次复杂的(脸由眼睛、嘴巴等构成;眼睛由眼睑、眼珠等构成;眼珠由晶状体、瞳孔等构成),人为的限制感受野,并进行由细微到全局的把控能缓解这种情况,但是如果某个细微实体的两种姿态被误判到两种“胶囊”中,又会引起整个模型更多的混淆
几何变换作为额外的信息输入,看似是不必要的(模型可以自己学到这种几何变换),但可以降低模型的学习门槛,并且对特征的学习起到了很好的约束
最终“胶囊”得到的输出可以用于表示图像的任意属性,比如通过带有光照干扰的自编码器,最终的“胶囊”输出将学会理解亮度,从而实现对场景照明及其方向的控制,而重要的是根据实验三可以发现,这种“胶囊”具备着强大的泛化能力