1 斜拉桥原理
例：固定绳子两端于点$(0,0)$和点$(a,b)$，并在绳子内任意位置悬挂重物，得到重物的坐标$(x,y)$，求$y$的最小值
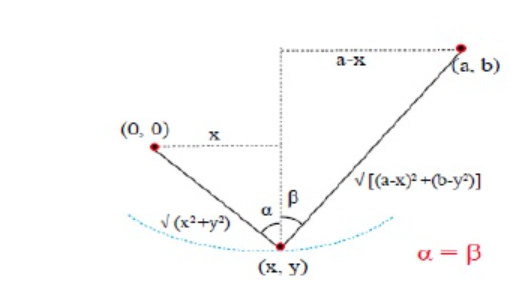
求解过程
- 根据题意可知$\sqrt{x^2+y^2}+\sqrt{(a-x)^2+(b-y)^2}=L$
- 悬挂重物轨迹曲线最低点处，切线水平，即$y'=0$
- 两边同时乘以$\frac{d}{dx}$可得（隐函数微分法）
$$\frac{1}{2}\frac{2x+2yy'}{\sqrt{x^2+y^2}}+\frac{1}{2}\frac{-2(a-x)-2(b-y)y'}{\sqrt{(a-x)^2+(b-y)^2}}=0$$
- 代入$y'=0$可得
$$\frac{x}{\sqrt{x^2+y^2}}=\frac{(a-x)}{\sqrt{(a-x)^2+(b-y)^2}}=0$$
- 由此可得$sin(\alpha)=sin(\beta)$，即$\alpha=\beta$
斜拉桥性质分析
- 此模型存在对称性，即$\alpha=\beta$，这使得绳两边受力一致
- 此状态下的绳子受力最少，断掉的可能性最小
- 这种悬挂模型的承重更平衡，分配重力最佳，因而广泛应用于造桥
拓展补充
- 这是属于椭圆曲线的性质
- 在DeCordava博物馆有一个迷你高尔夫之一杆入洞的项目
- 发球台在椭圆的一个焦点，球洞在椭圆的另一个焦点，发球必入洞！
2 牛顿迭代法 newton's method
借助导数值迭代计算函数的解
- 选择迭代初始值$x_1$，此时$n=1$
- 计算函数值$f(x_n)$及其一阶导数值$f'(x_n)$
- 根据以下公式，计算$x_{n+1}$和$y_{n+1}$
$$x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}$$ $$y_{n+1}=y_n+f'(x_n)(x_{n+1}-x_n)$$ 4. 更新$n=n+1$，并重复2、3步骤，直至函数值收敛
算法图示如下：
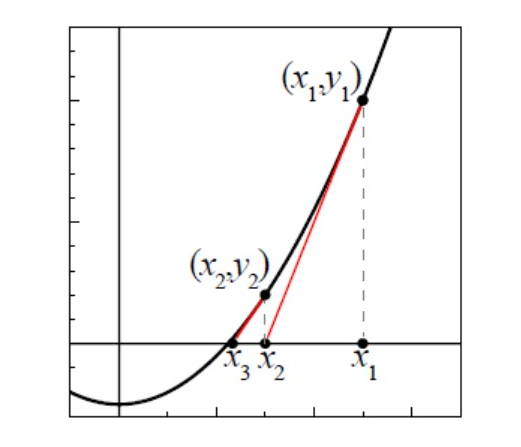
更多细节可参阅[[1_study/algorithm/迭代优化算法/拟牛顿类算法]]
3 参考
youtube - Elliptical Pool Table - Numberphile
