1 定积分(definite integral)
$$\int_a^bf(x)dx=F(b)-F(a)$$
- 其中$F(x)$是$f(x)$的原函数,$[a,b]$是$x$的区间范围
- 相比于不定积分有区间上下限的限制,排除了常数$c$
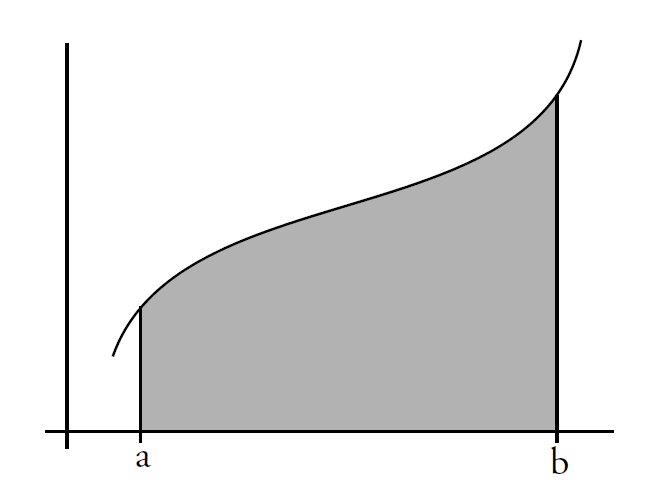
- 定积分表示在某个区间上函数曲线与$x$轴所围成的面积
2 定积分通解-面积近似法
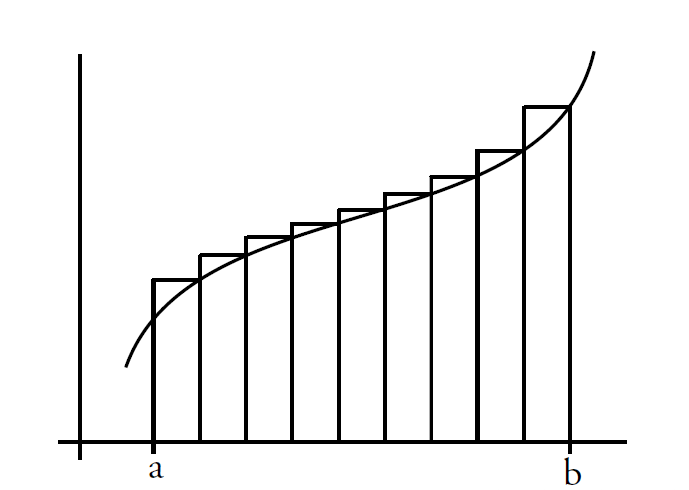
- 沿着$x$轴垂直切割图像,然后得到很多矩形
- 多个矩形面积的加和就是面积的近似值
3 定积分求解
例:计算$y=x^2$从$0$到$b$的面积
解析解
- $\int x^2dx=\frac{x^3}{3}+c$
- $\int_0^bx^2dx=(\frac{b^3}{3}+c)-(\frac{0^3}{3}+c)=\frac{b^3}{3}$
面积近似
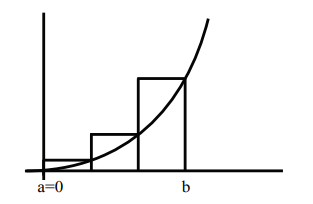
- 在0到b之间划分为n份
$$\begin{align} S & \approx \frac{b}{n}f(\frac{b}{n})+\frac{b}{n}f(\frac{2b}{n})+...+\frac{b}{n}f(\frac{nb}{n}) \ \\ & = \frac{b}{n}(\frac{b}{n})^2+\frac{b}{n}(\frac{2b}{n})^2+...+\frac{b}{n}(\frac{nb}{n})^2 \ \\ & = (\frac{b}{n})^2(1+2^2+3^2+...+n^2) \end{align}$$
- 其中$(1+2^2+3^2+...+n^2)$可以通过几何法快速求解
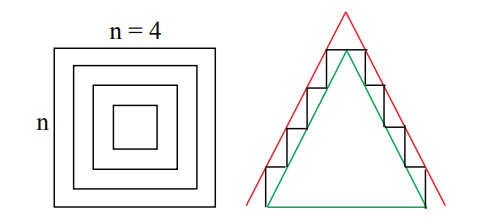
- $(1+2^2+3^2+...+n^2)$可以看作高为$1$的砖块堆砌$n$层的金字塔体积
- 金字塔体积最底层体积为$1\times n^2$,最高层体积为$1$
- 金字塔体积$V$介于两个锥体之间(即下图中绿色锥体和红色锥体)
- 由此可得$\frac{n^3}{3}<V<\frac{(n+1)^3}{3}$
- $S=(\frac{b}{n})^2V$,随着$n\to \infty$,可得$S=\frac{b^3}{3}$
4 黎曼和(Riemann sum)
$$\lim_{\Delta \to 0}\Sigma_{i=1}^nf(x_i)\Delta x=\int_a^bf(x)dx$$
积分可以解释为一种累积和
应用:计算欠款累积
- 设本金为$P$,利率为$r$,则经过时间$T$后,总欠款为$Pe^{rT}$
- 假设每天借一次钱,每次借钱数符合函数$f(t)$,单位是 "美元/年"
- 年末欠款累积为$\Sigma_{i=1}^{365}[f(\frac{i}{365})\Delta t]e^{r(1-\frac{i}{365})}=\int_0^1f(t)e^{r(1-\frac{i}{365})}dt$
- 其中$i$表示第$i$天借款,距离还款天数为$(365-i)$;$\Delta t=\frac{1}{365}$年
5 参考