1 斜拉桥原理
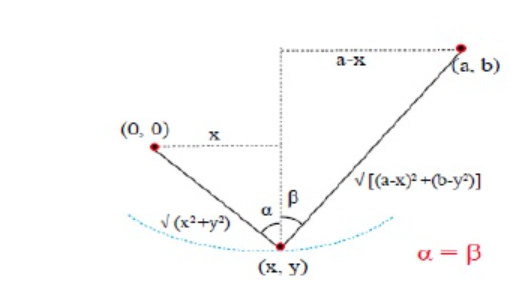
例:固定绳子两端于点$(0,0)$和点$(a,b)$,并在绳子内任意位置悬挂重物,得到重物的坐标$(x,y)$,求$y$的最小值
求解过程
- 根据题意可知$\sqrt{x^2+y^2}+\sqrt{(a-x)^2+(b-y)^2}=L$
- 悬挂重物轨迹曲线最低点处,切线水平,即$y'=0$
- 两边同时乘以$\frac{d}{dx}$可得(隐函数微分法)
$$\frac{1}{2}\frac{2x+2yy'}{\sqrt{x^2+y^2}}+\frac{1}{2}\frac{-2(a-x)-2(b-