1 斯托克斯定理
关于格林公式的前置知识可参考之前的第22课时内容和第23课时内容
格林公式可以看作斯托克斯(Stokes)定理在$xy$平面下的特例
当$C$为闭合曲线,包围着曲面$S$,则斯托克斯(Stokes)定理可表示如下: $$∮_C\vec{F}\cdot d\vec{r}=\int \! \! \!\int_Scurl(\vec{F})\cdot d\vec{S}=\int \! \! \!\int_S(\nabla \times \vec{F})\cdot \hat{n}dS$$ 其中向量$\hat{n}$表示曲面的法向量,其方向的确定需要满足右手定则:
- 将右手拇指指向曲线$C$的方向
- 将右手食指指向曲面$S$(相对曲线$C$来说的内侧)
- 则右手中指将指向法向量$\hat{n}$的方向
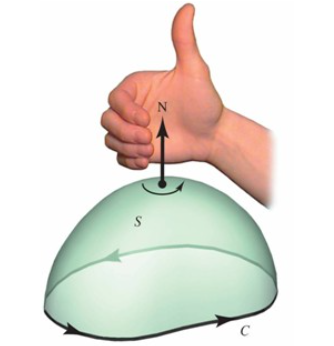
在网上查阅到了右手定则的另一种形式,相对更加简单直观:
注意:斯托克斯定理并没有对曲面$S$作约束限制,当曲线$C$为圆圈时,被$C$约束边界的曲面$S$可以是半球状的、圆锥状的。这种情况和之前讲解的路径独立(做功只取决于起止点,与路径无关)很相似,在下一课时中将针对这种曲面的独立性进行进一步讨论
2 斯托克斯定理的证明
本小节不再给出斯托克斯定理的完整证明,只是阐述证明的大致内涵:
- 将斯托克斯定理约束在平面内时,即转化为格林公式
- 格林公式的证明在第22课时中有较为详细的阐述
- 功、通量、旋度等都是有实际意义的,不取决于预设的坐标系
- 对于复杂三维空间中的曲面,可以转化为$N$个小平面分别求解并汇总
3 参考