1 格林公式
假设$C$为逆时针的封闭曲线,包围着区域$R$;如果向量场$\vec{F}$在曲线$C$和区域$R$处处有定义且处处可微,则存在格林公式使得线积分转化为双重积分: $$∮_c\vec{F}\cdot d\vec{r}=\int \! \! \!\int_Rcurl(\vec{F})dA$$ 坐标形式的格林公式: $$∮_cMdx+Ndy=\int \! \! \!\int_R(N_x-M_y)dA$$
此处限制曲线$C$为逆时针是一种人为规定的方向,也就是一种约定成俗。就好像定义旋度$=N_x-M_y$,而不是$M_y-N_x$一样。
2 格林公式示例
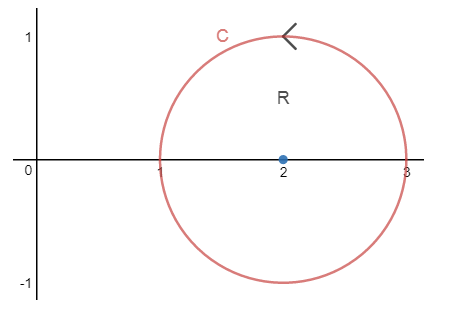
假设曲线$C$为圆型的逆时针曲线,圆心坐标为$(2,0)$,半径为$1$,请计算线积分 $$∮_c\vec{F}\cdot d\vec{r}=∮_c(ye^{-x}dx+(\frac{1}{2}x^2-e^{-x}dy)$$
分析:由于$N_x \neq M_y$,所以判断不是保守场。
- 考虑直接进行变量替换:$x=2+cos(\theta),y=sin\theta$
- 带入后结果较为复杂,暂时PASS掉
- 满足格林公式的前提假设,考虑带入公式可得
$$∮_c\vec{F}\cdot d\vec{r}=\int \! \! \!\int_R(N_x-M_y)dA=\int \! \! \!\int_R[(x+e^{-x})-e^{-x})]dA$$ 4. 正常情况下,此时可以计算上下限后,依次求解双重积分 5. 不过此题存在简便运算技巧: $$\int \! \! \!\int_RxdA=Area(R)\cdot \overline{x}=2\pi$$
3 格林公式证明
思路:从特例推广到一般
先考虑$N=0$且区域简单的特殊情况
假设区域$R$是竖直简单的,并且边界为逆时针曲线$C$。区域$R$的公式化描述如下: $$a<x<b,f_1(x)<y<f_2(x)$$

此时线积分公式可拆分为四个部分($c_1,c_2,c_3,c_4$): $$\begin{align} ∮_c\vec{F}\cdot d\vec{r}
& =\int_{c_1}Mdx+\int_{c_2}Mdx+\int_{c_3}Mdx+\int_{c_4}Mdx \ \\ & = 0 -\int_a^bM(x,f_2(x))dx + 0 + \int_a^bM(x,f_1(x))dx \end{align}$$ 另一方面,可对$\int \! \! \!\int_R-M_ydA$进行变换: $$\int \! \! \!\int_R-M_ydA=-\int_a^b \! \! \!\int_{f_1(x)}^{f_2(x)}\frac{\partial{M}}{\partial{y}}dydx=\int_a^b[M(x,f_1(x)) -M(x,f_2(x))]dx =∮_c\vec{F}\cdot d\vec{r}$$ 所以在此条件下,格林公式成立: $$∮_c-Mdy=\int \! \! \!\int_RM_ydA$$
同理可证$M=0$且区域简单的特殊情况,格林公式成立: $$∮_cNdy=\int \! \! \!\int_RN_xdA$$
验证可加性,得到完整的格林公式
如下图所示,考虑将曲线$C$切分成$C_1$和$C_2$:
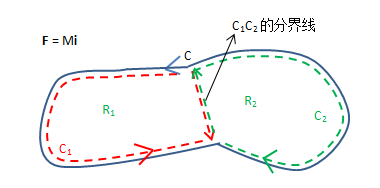
由于$C_1$和$C_2$在分界线处方向相反,所以分界线处的线积分结果可互相抵消,即:$$∮_cMdx=∮_{c_1}Mdx+∮_{c_2}Mdx$$ 所以对应复杂区域,总是可以通过切分的方式转化为多个简单的区域,再结合前两步所得结论,格林公式得证
拓展科普:测面器
一种通过绘制闭合曲线即可测量出曲线内面积的仪器,在计算机兴盛前常用于生物化学实验中进行辅助计算,后来由于成本高昂(几千美元一台)被逐渐取代。测面器的核心原理就是借助了格林公式:$∮_cxdy=\int \! \! \!\int_R1dA=Area(R)$
4 参考: