中文标题:针对时序数据挖掘的新方法-Shapelets
英文标题:Time Series Shapelets:A New Primitive for Data Mining
发布平台:SIGKDD
Proceedings of the 15th ACM SIGKDD international conference on Knowledge discovery and data mining
发布日期:2009-06-28
引用量(非实时):1143
DOI:10.1145/1557019.1557122
作者:Lexiang Ye, Eamonn Keogh
关键字: #时间序列 #shapelets #数据挖掘
文章类型:conferencePaper
品读时间:2021-12-31 14:50
1 文章萃取
1.1 核心观点
对于大部分时序聚类问题来说,KNN等简单分类算法是不适用的,因为这类算法对于整个数据的存储和搜索都有较高的时间复杂度和空间复杂度,并且最终结果的可解释性不够强。本文引入了一种叫做
time series shapelets的新方法,通过寻找时序的最优子序列的方式解决了以上两点问题,实现了更高效、更精准、结果可解释性更强的分类方法。
1.2 综合评价
- 内容循序渐进,通过子序列早弃和熵剪枝逐步优化算法性能
- 构建出可解释性高的子序特征shaplets,应用领域广泛,属于奠基性文章
- 在高维数据上依然存在过长耗时问题,仅针对二分类问题(可优化)
- 考虑历史的局限性,对比的算法KNN过于简单,模型测试角度也不太全面
1.3 主观评分:⭐⭐⭐⭐
2 精读笔记
2.1 shapelets入门
以荨麻草(urtica dioica)和马鞭草(Verbena urticifolia)的分类为例
马鞭草也被称为“假荨麻”,和荨麻草非常的相似,并且还会因为bug(虫子)导致数据产生噪音。

首先将叶子的轮廓转化为一维时序
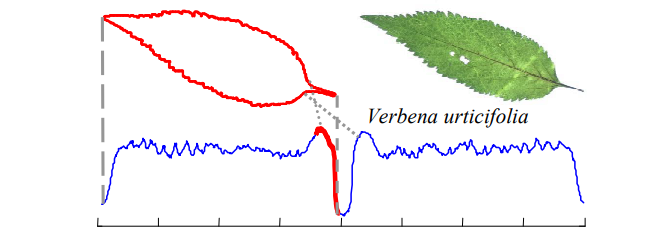
轮廓转化为一维时序的方法说明补充:
- 将轮廓转化为坐标值,并计算中心点
- 计算轮廓坐标到中心点的距离作为一维时序值
- 同一类图片以最小距离为原则寻找最优的旋转角度,实现旋转不变性
基于shapelets的分类思路核心在于,寻找到最优(最能区分两个类别)的子时序
比如叶柄与叶子外轮廓间的夹角,这是两种植物最显著的区分点:
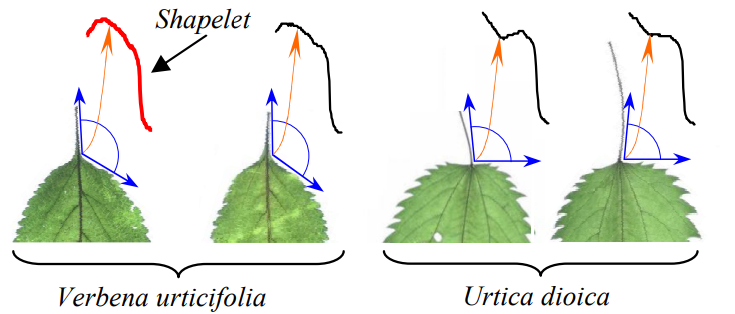
而找到这类特征后,就可以构建一个简单的模型用于分类,比如决策树:
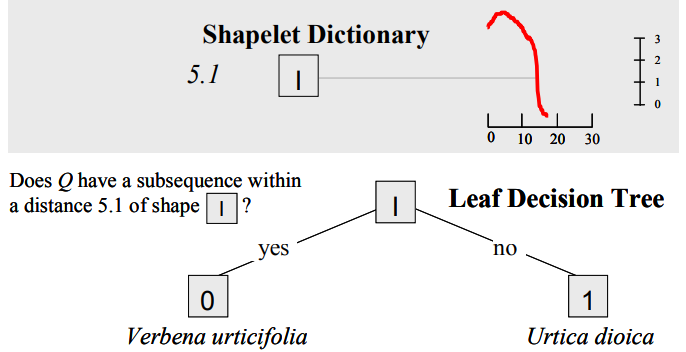
优点:
- 结果天然具有可解释性,特征是可视化的,方便理解
- 相比于全局特征,借助局部特征建模准确性、稳健性更高
- 在保证性能的情况下,速度快,时间复杂度为$O(ml)$,其中
m是输入时序的长度,l是shaplet的长度。而当时性能最好的全局测度的DTW算法,时间复杂度为$O(km^3)$ ,其中k为训练集中的引用对象个数。
2.2 背景知识
| 符号 | 解释 | |
|---|---|---|
| $T$ | 长度为$m$的时间序列:$T=t_1,...,t_m$ | |
| $S$ | 从$t_p$长度为$l$的$T$的子序列:$S=t_p,...,t_{p+l-1}$ | |
| $S_T^l$ | 通过长度为$l$的滑动窗口,得到的时序$T$的子序列集合 | |
| $SubsequenceDist(T,S)$ | 子序列$S$与序列$T$之间的距离=$min(Dist(S,S'))\ \ for \ \ S'\in S_T^{m}$ | |
| $D$ | 数据集,包含两种类别A与B | |
| $I(D)$ | 数据集的熵$=-p(A)log(p(A))-p(B)log(p)(B))$ | |
| $Gain(sp)$ | 将数据集$D$划分为$D_1$和$D_2$的信息增益 | |
| $d_{th}$ | 可与距离比较的阈值,通过比较$SubsequenceDist(T,S)$和$d_{th}$来切分数据集 | |
| $OSP$ | 最优的切分策略,此时$Gain(S,d_{OSP(D,S)})\geq Gain(S,d_{th}')$,其中$d_{th}'$表示任意的阈值 | |
| $Shapelet(D)$ | 最优切分策略下的最优子序列,此时对于任意的子序列$S$,$Gain(shapelet(D),d_{OSP(D,shapelet(D))})\geq Gain(S,d_{OSP(D,S)}')$ | |
| $MINLEN, MAXLEN$ | 滑动窗口的最小长度和最大长度 | |
| $m_i$ | 数据集$D$包含$k$个时序,其中第$i$个时序$T_i$的长度为$m_i$ | |
| $\Sigma_{l=MINLEN}^{MAXLEN}\Sigma_{T_i\in D}(m_i-l+1)$ | 表示所有可能产生的候选子序列个数 | |
直观理解1:计算所有子序列与所有时序的距离,距离通过阈值判断将时序分类,$shapelet$就是最优的阈值情况下最优的子序列,这里的最优是通过比较分类前后的信息增益得到的
直观理解2:所有的候选子序列其实会非常多,比如时序数为200,时序长度为275的数据集,在规定滑动窗口范围为3~275的情况下,最终的候选子序列个数有7480200之多。因此后文会针对此问题进行算法上的优化~
2.3 算法-寻找shapelet
2.3.1 辅助函数
- 生成所有可能的候选子序列

- 针对给定的一个候选子序列,计算它与所有时序的距离,并存储到变量
obejct_histogram中

- 根据距离构成的列表,以信息增益最大为原则,寻找最优切分阈值

2.3.2 暴力枚举
- 遍历候选子序列,寻找信息增益最大的子序列

2.3.3 优化1:子序列早弃
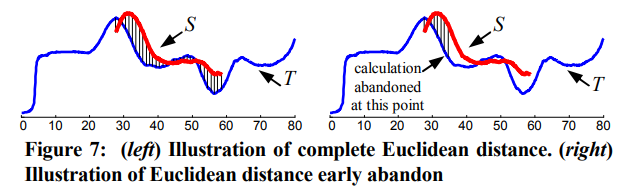
- 在蛮力法中,计算时序T到子序列S的距离,需要先找到T中每个长度为|S|的子序列,并计算其与S的欧氏距离,然后选择距离的最小值作为时序T到子序列S的距离
- 子序列早弃法的核心思想在于对距离计算的优化,当处于累加中的距离高于之前的最小值时,就放弃继续计算,这样虽然计算复杂度的量级依然是O(|T|),但是常数因子显著降低
- 最终子序列早弃的伪代码如下:

2.3.4 优化2:熵剪枝
- 信息增益的计算复杂度要远低于距离的计算复杂度,所以可以通过提前计算信息增益的方式,避免后续的距离计算过程。具体过程以示例的形式说明:
- 首先有一个当前最优的信息增益案例:

- 然后根据新的子序列进行分类时,进行到一半的情况(分类了5个)可能如下:

- 这时假设后续分类情况是最优的,即后续的5个序列分类结果,蓝/红的全在左/右边

计算这种情况下的信息增益,可得结果为0.2911,低于之前的最大信息增益,因此不再考虑对此案例进行继续的分类和距离计算,可以直接舍弃
最终熵剪枝的伪代码如下:

2.4 基于shapelets的分类算法
- 主要借鉴了决策树的思路,只不过把原本结点的特征选择改为了shaplets选择

- 对应的准确度计算也非常简单

2.5 模型评估
2.5.1 耗时评估
- 以闪电EMP分类数据为例,其每条时序的长度为2000条
- 随着数据量增长,不同方法的耗时结果如下
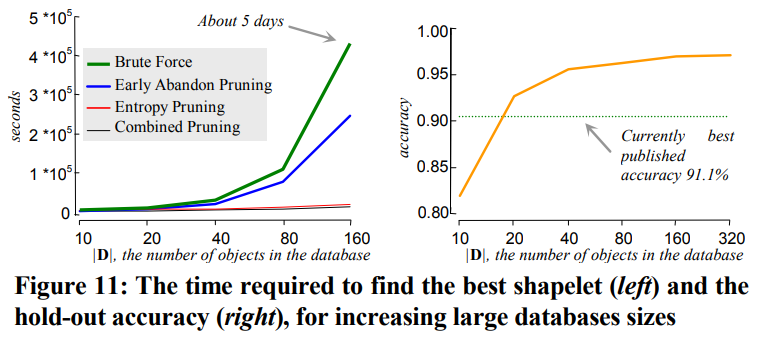
- 暴力枚举法(绿)基本不具备实用价值,仅160条时序就需要耗时5天
- 相比于暴力枚举法,早弃法(蓝)有明显的效率提升(降低耗时接近一半)
- 相比于早弃法,熵剪枝(红)有非常明显的效率提升(降低耗时接近两个数量级)
- 最优的方法是早弃法与熵剪枝的结合(黑),耗时略低于熵剪枝
2.5.2 准确度
主要与基于旋转不变性的最邻近算法(KNN,本论文中K=1)比较
| 数据集 | 旋转不变1NN算法(准确度) | Shaplets分类决策树(准确度) |
|---|---|---|
| 箭头分类 | 68% | 80% |
| 盾牌分类 | 82.9% | 89.9% |
| 小麦光谱分类 | 44.1% | 72.6% |
