中文标题:基于趋势特征表示的shapelet分类方法
英文标题:Shapelet classification method based on trend feature representation
发布平台:计算机应用
Journal of Computer Applications
发布日期:2017-08-10
引用量(非实时):0
DOI:10.11772/j.issn.1001-9081.2017.08.2343
作者:闫欣鸣,孟凡荣,闫秋艳
关键字: #时间序列 #shapelets #TDTS
文章类型:journalArticle
品读时间:2022-01-05 10:44
1 文章萃取
1.1 核心观点
本论文提出了一种基于趋势特征的多样化top-k shapelet分类方法:首先采用趋势特征符号化方法提取趋势信息;然后针对趋势特征符号获取shaplet候选集合;最后引入top-k查询算法选择k个最具代表性的shaplets。最终结果的准确率和算法效率均有提升,并且保留了趋势信息。
1.2 综合评价
- 借助Hash碰撞去除了部分冗余计算,(针对长时序数据)计算性能进行改善
- 借助趋势的特征符号化保留shapelets的趋势信息
- 引入图用于剔除top-k shapelets的相关性,但
- 部分描述略显含糊,比如碰撞得分函数的定义、趋势信息的离散化过程
- 额外引入了超参-相似度阈值、r(随机覆盖次数)、M(得分最高的M个序列)等
1.3 主观评分:⭐⭐⭐
2 精读笔记
2.1 引言
shaplet是指时间序列某一段子序列,是具有辨析度的局部特征
最初的shaplets(阅读本文前建议先阅读此论文)不能胜任多分类的任务,并且性能存在优化的空间。后来者通过各种方式逐步克服了以上种种困难,使得shaplet更加的高效易用。而本论文则是从保留趋势信息的角度,对shapelets提出了新的优化思路。
| 符号 | 解释 | |
|---|---|---|
| $T$ | 长度为$m$的时间序列:$T=t_1,...,t_m$ | |
| $S$ | 从$t_p$长度为$l$的$T$的子序列:$S=t_p,...,t_{p+l-1}$ | |
| $S_T^l$ | 通过长度为$l$的滑动窗口,得到的时序$T$的子序列集合 | |
| $SubseqDist(T,S)$ | 子序列$S$与序列$T$之间的距离=$min(Dist(S,S'))\ \ for \ \ S'\in S_T^{m}$ | |
| $D$ | 数据集,包含的第$i$个类别为$C_i$ | |
| $E(D)$ | 数据集的熵$=-\Sigma(p(C_i)log(p(C_i)))$ | |
| $IG$ | 信息增益 | |
| $d_{th}$ | 可与距离比较的阈值,通过比较$SubseqDist(T,S)$和$d_{th}$来切分数据集 | |
| $OSP$ | 最优的切分策略,此时$Gain(S,d_{OSP(D,S)})\geq Gain(S,d_{th}')$,其中$d_{th}'$表示任意的阈值 | |
| $Shapelet(D)$ | 最优切分策略下的最优子序列,此时对于任意的子序列$S$,$Gain(shapelet(D),d_{OSP(D,shapelet(D))})\geq Gain(S,d_{OSP(D,S)}')$ | |
| $min, max$ | 滑动窗口的最小长度和最大长度 | |
| $m_i$ | 数据集$D$包含$k$个时序,其中第$i$个时序$T_i$的长度为$m_i$ | |
| $\Sigma_{l=MINLEN}^{MAXLEN}\Sigma_{T_i\in D}(m_i-l+1)$ | 表示所有可能产生的候选子序列个数 | |
| $shapelet相似$ | 任意两个$shapelet(S_1,d_1)$和$shapelet(S_2,d_2)$,相似意味着$SubseqDist(S_1,S_2)<max(d_1,d_2)$ | |
| $I$ | 候选$shapelet$集合,$I={S_1,S_2,...,S_n}$ | |
| $G(I)=(V,E)$ | 多样化图,其中$V$是所有候选$shapelet$可能构建的顶点集合,$E$是两点之间的边,描述两个候选$shapelet$之间是否相似 | |
| $DivTopk(I)$ | $多样化top-k / shapeletes$,从候选集合中选择总分最高并且互不相似的$k$个$shapelet$ |
2.2 趋势特征表示的shapelet分类
趋势特征表示的shapelet分类方法,简称TDTS
- 首先采用趋势特征符号化方法提取趋势信息
- 然后针对趋势特征符号获取shaplet候选集合
- 最后引入top-k查询算法选择k个最具代表性的shaplets。

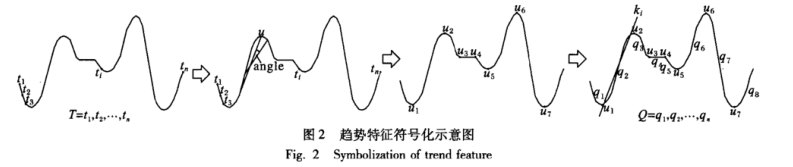
2.2.1 趋势特征符号化
- 通过滑动窗口机制计算斜率,当斜率超过一定阈值后分段
- 找出所有分段点,对每一段子序列进行符号化
- 每一段子序列转化为一个二元组$<K,u>$,其中$K$表示斜率,$u$表示终点值
- 对二元组的连续值进行离散化处理,比如$K=-5$表示角度在$(-50°,-40°)$之间
- 最后返回已经经过趋势特征符号化处理的TFSA序列集
最终的二元组分别代表斜率和截距,是描述一条直线的最简方式
伪代码如下所示:

通过参数num限制,确保最终的TFSA序列都是等长的
2.2.2 基于趋势特征的shapelet快速发现
- 不同于暴力枚举法,shapelet的快速发现主要通过Hash碰撞检测实现的
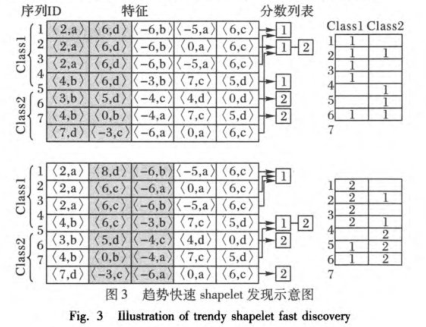
- 上图左侧表示同一组序列的两次随机遮掩后的情况,右侧则记录了碰撞频次
- 针对给定的候选集合
TFSAList中给定每一个序列,先进行部分特征的随机遮掩(暗色部分) - 针对非遮掩部分通过碰撞测试进行相似度评估,最优的情况是同类内的序列都会碰撞到,不同类间的序列都不会碰撞到(这里的碰撞其实就是指是否存在相同的二元组$<K,u>$)。
- 而上图的实际情况是,第一次碰撞测试中,
Class1中的样本2与Class2中的样本7发生了非理想碰撞;第二次碰撞测试中,Class1中的样本4与Class2中的样本6发生了非理想碰撞 - 针对碰撞情况构建得分
score函数用于寻找类内碰撞最多,类间碰撞最少的序列(文中未明确定义,但个人觉得定义类似于TFIDF的计算方式,一种可能的简单形式如下:得分 = (类内碰撞次数-类间碰撞次数)/总次数) - 最终将得分最高的M个序列作为候选序列,重新映射到原数据集上,然后产生候选shapelets并计算相应的信息增益
总结来说,就是先通过Hash碰撞得分选择最具备代表性的M个序列,然后基于此M个序列对应的原始序列产生候选shapelets,这样做能极大地降低了候选shapelets的数量
最终伪代码如下:

RandProjection函数表示Hash碰撞过程,返回碰撞次数的统计情况UpdateScore函数用于得分的计算,类内碰撞最多,类间碰撞最少,得分越高FindTopKTFSA函数用于寻找得分最高的M个序列,本文中M=10Remap函数用于将TFSA序列重新映射到原数据集上,并生成所有的shapelets候选CalInfoGain函数用于计算shapelets候选对应的信息增益- 变量r表示随机掩盖次数,也是Hash碰撞的次数,本文中r=10
2.2.3 多样化top-k shapelets查询

- 多样化图的引入主要是为了去除top-k shapelets间的相关性
具体伪代码如下:

- 根据候选shapelets构建图,其中顶点表示shaplets,边表示两个shapelets是相似的
- 遍历已排序(信息增益由大到小)的候选shapelets,寻找前k个互不相关的shapelet
vi.adj(Graph)表示Graph中节点vi的邻接节点
2.3 实验结果分析
选择了 11份数据集和7种常见算法,对比结合TDTS前后的表现,说明了TDTS的有效性
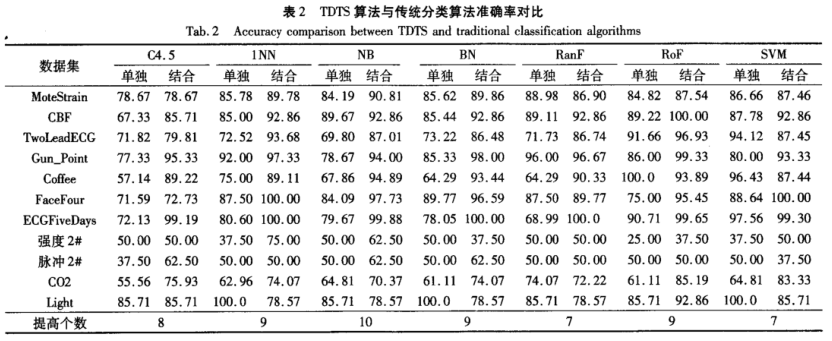
与FastShapelet算法进行运行时间的对比,论证了TDTS算法在长时序数据集中会有明显的性能改善