1 维特比算法概述
维特比算法(Viterbi algorithm)是一种寻找最短路径的动态规划算法。可以用于寻找最有可能产生观测事件序列的维特比路径——隐含状态序列,适应于多步骤每步多选择模型的最优选择问题,比如HMM。
2 维特比算法核心
维特比算法是针对暴力枚举法的优化
假设有一个长度为$l$的序列,其中$l$对应总天数
其中第$i$天的隐含状态可能情况有$n$种,第$i+1$天的隐含状态可能情况有$m$种
第$i$天的最大概率为$P_i=argmax_k({P_{ik}},k=1,...,n)$,其中$P_{ik}$表示第$i$天隐含状态$k$的最大概率,而第$i+1$天的最大概率$P_{i+1,j}=argmax_j({P_{i+1,j}},j=1,...,m)$,,其中$P_{i+1,k}$表示第$i+1$天隐含状态$k$的最大概率,则 $$P_{i+1,j}=argmax_k({P_{i,k}\times T_{k,j}},k=1,...,n,j=1,...,m)$$
其中$T_{kj}$表示隐含状态从$k$到$j$的转移概率
通过这种方式,第$i+1$天的最大概率就不用再从头开始了,而是基于第$i$天的结果继续计算,减少了计算成本。
将乘法转为加法,最大概率转为最短距离,此时这就是一个最短距离问题了。
3 维特比算法示例
承接1_study/algorithm/概率图类模型/隐马尔可夫模型 HMM:
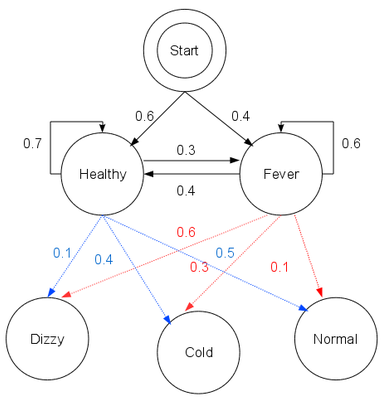
现在有个病人连续三天来看医生,第一天正常,第二天发寒,第三天头晕
那么这个病人最近这三天每一天的状态到底是健康还是发烧呢?
将连续三天,每天两种状态表述为下图的形式,由左到右的每一条完整路径都是一个维特比路径,每一条维特比路径都对应着一种状态的可能组合,比如{健康,生病,健康} 或 {生病,生病,生病}
已知初始状态及其概率为{健康0.6,发烧0.4}
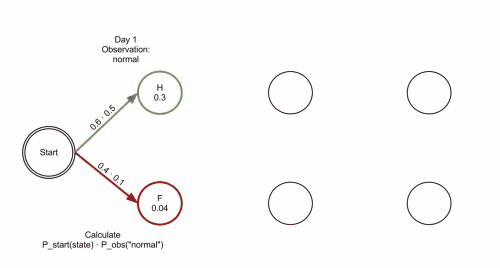
当第一天的健康状况为正常时:
- 第一天健康状态概率为$0.6\times 0.5=0.3$
- 第一天发烧状态概率为$0.4\times 0.1=0.04$
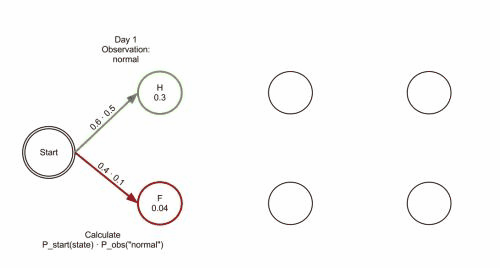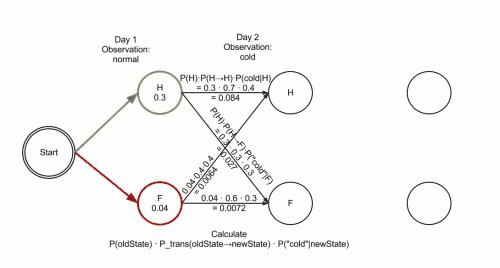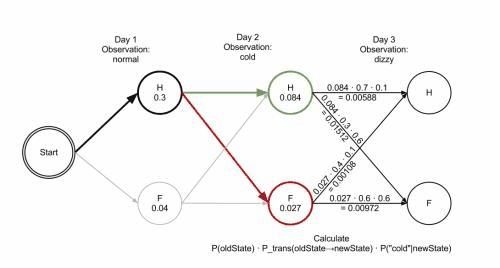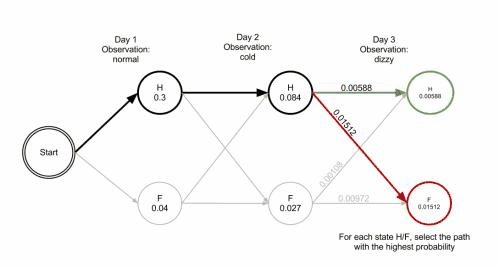
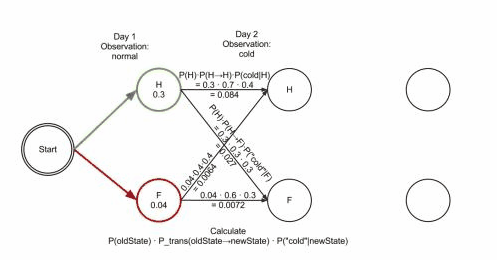
当第二天的健康状况为发寒时:
假设第一天是健康状态:
- 第二天继续保持健康状态并且发寒的概率为$0.3*0.7*0.4=0.084$
- 第二天健康转为发烧状态并且发寒的概率为$0.3*0.3*0.3=0.027$
假设第一天是发烧状态:
- 第二天继续保持发烧状态并且发寒的概率为$0.04*0.6*0.3=0.0072$
- 第二天发烧转为健康状态并且发寒的概率为$0.04*0.4*0.4=0.0064$
- 第二天健康状态最大概率为$0.084$
- 第二天发烧状态最大概率为$0.027$
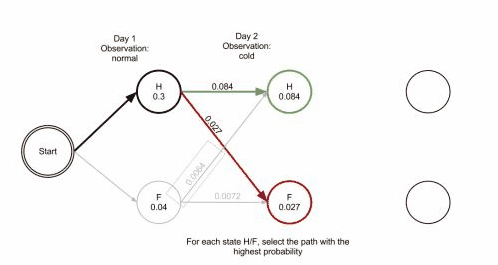
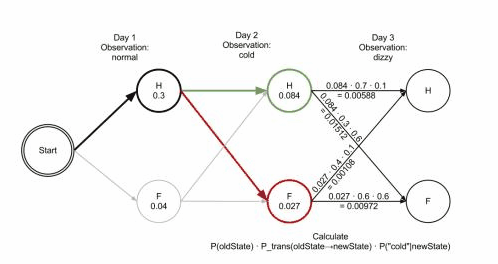
当第三天的健康状况为头晕时:
假设第二天是健康状态:
- 第三天继续保持健康状态并且头晕的概率为$0.084*0.7*0.1=0.00588$
- 第三天健康转为发烧状态并且头晕的概率为$0.084*0.3*0.6=0.01512$
假设第二天是发烧状态:
- 第三天继续保持发烧状态并且头晕的概率为$0.027*0.6*0.6=0.00972$
- 第三天发烧转为健康状态并且头晕的概率为$0.027*0.4*0.1=0.00108$
注意,此时不需要再考虑第一天的可能性,这就是维特比算法的计算优势
- 第三天健康状态最大概率为$0.00588$
- 第三天发烧状态最大概率为$0.01512$
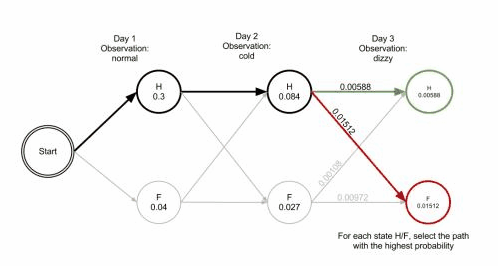
所以观察值序列为{正常,发寒,头晕}的病人最有可能的状态序列是
{健康,健康,发烧}
最后总结动图如下: