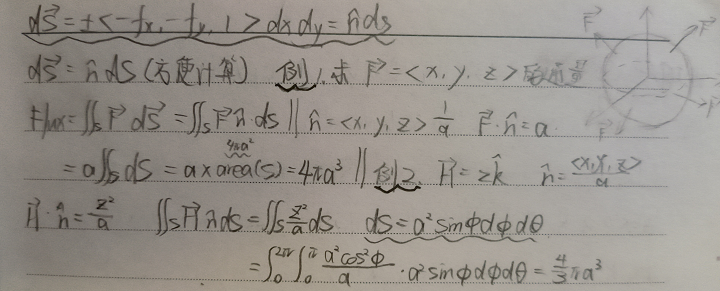1 三维向量场
与平面向量场类似,只不过维度为三: $$\vec{F}=x\vec{i}+y\vec{j}+z\vec{k}=<x,y,z>$$
2 通量与面积分
三维向量场下的通量 - 描述单位时间内流体场$\vec{F}$通过表面$S$的流量:
$$Flux=\int \! \! \! \int _S\vec{F}d\vec{S}=\int \! \! \! \int _S\vec{F}\hat{n}dS$$
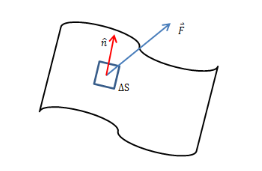
- 其中$\hat{n}$为面$S$的法向量
- $dS$表示面积积元,和实际的切分方式有关
- 常通过面积分进行通量的计算
3 面积分的计算
示例1:求向量场$\vec{F}=<x,y,z>$在半径为$a$的球面上的通量
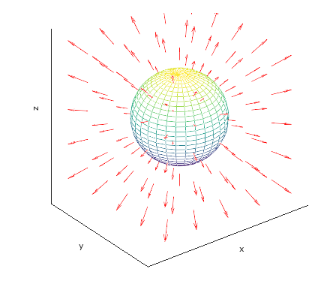
分析:
- 球面的单位法向量是$\hat{n}=\frac{1}{a}<x,y,z>$
- 球面上法向量处处与向量场平行
- 球面上的坐标满足公式:$\sqrt{x^2+y^2+z^2}=a$
$$Flux=\int \! \! \! \int _S\vec{F}\hat{n}dS=\int \! \! \! \int _S|\vec{F}|dS=a\int \! \! \! \int _SdS=a\times4\pi a^2=4\pi a^3$$
注意公式中的$\int !!! \int _SdS$其实就是指球的表面积
示例2:求向量场$\vec{F}=<0,0,z>$在半径为$a$的球面上的通量
分析:
- 先计算法向量与向量场的点乘:$\vec{F}\cdot \hat{n}=<0,0,z>\cdot \frac{1}{a}<x,y,z>=\frac{z^2}{a}$
- 面积积元$dS$需要借助球坐标系进行参数转换
$$Flux=\int \! \! \! \int _S\vec{F}\hat{n}dS=Flux=\int \! \! \! \int _S\frac{z^2}{a}dS$$ 带入参数转换关系$dS=a^2sin\phi d \phi d\theta,z=a cos\phi$,可得: $$\int \! \! \! \int _S\frac{z^2}{a}dS=\int_0^{2\pi}\int_0^{\pi}\frac{a^2cos^2\phi}{a}a^2sin\phi d \phi d\theta=\frac{4}{3}\pi a^3$$
当向量场只沿着$z$轴方向时,经过球面的流量值等于高度为1的圆柱体面积
4 参考